
- •Обчислення потрійного інтеграла.
- •Потрійний інтеграл у циліндричних і сферичних координатах.
- •Застосування потрійного інтеграла до задач геометрії.
- •Застосування потрійного інтеграла до задач механіки і фізики.
- •Криволінійні інтеграли першого роду: означення, його існування, обчислення, властивості.
- •Застосування криволінійного інтеграла першого роду: Маса матеріальної кривої, центр маси, момент інерції.
- •Криволінійні інтеграли першого роду для просторових кривих.
- •Криволінійні інтеграли другого роду: означення, його існування, обчислення, властивості.
- •Криволінійні інтеграли другого роду вздовж просторових кривих.
- •Формула Гріна. Обчислення площі плоскої фігури через криволінійний інтеграл.
- •Поверхневі інтеграли першого роду: означення, обчислення.
- •Деякі застосування поверхневих інтегралів до механіки.
- •Поверхневі інтеграли другого роду. Зв'язок між поверхневими інтегралами і і II роду.
- •Формула Остроградського-Гауса. Формула Стокса.
- •Скалярне поле. Характеристики скалярного поля. Градієнт.
- •Векторне поле. Потік векторного поля. Дивергенція векторного поля. Циркуляція векторного поля. Ротор векторного поля.
- •Спеціальні векторні поля. Потенціальне поле. Соленоїдальне поле.
- •Поняття числового ряду. Збіжність і сума ряду. Основні властивості збіжних рядів. Необхідна ознака збіжності ряду.
- •2. Деякі властивості числових рядів.
- •3. Необхідна ознака збіжності ряду
- •Достатні ознаки збіжності додатних рядів
- •Візьмемо другий додатний числовий ряд, збіжність чи розбіжність якого відома (11)
- •Знакозмінні ряди. Абсолютна та умовна збіжності рядів
Обчислення потрійного інтеграла.
Обчислення потрійного інтеграла зводять до обчислення повторних, тобто до інтегрування за кожною змінній окремо.
Нехай
область D
обмежена знизу
і зверху поверхнями
![]() і
і
![]() ,
а з боків циліндричною поверхнею, твірні
якої паралельні осі
,
а з боків циліндричною поверхнею, твірні
якої паралельні осі
![]() .
Позначимо
проекцію області G
на площину
.
Позначимо
проекцію області G
на площину
![]() через D
(рис. 1) і вважатимемо, що функції
через D
(рис. 1) і вважатимемо, що функції
![]() і
і
![]() неперервні в D.
неперервні в D.

Рисунок 1 – Область G
Якщо
при цьому область D
є правильною,
то область G
називається
правильною у напрямі осі Oz.
Припустимо,
що кожна пряма, яка проходить через
кожну внутрішню точку
![]() паралельно осі Oz,
перетинає межу
області G
у точках M
і N.
Точку M
назвемо точкою
входу в область
паралельно осі Oz,
перетинає межу
області G
у точках M
і N.
Точку M
назвемо точкою
входу в область
![]() G,
а точку N
– точкою виходу з області G,
а їхні аплікати позначимо відповідно
через
G,
а точку N
– точкою виходу з області G,
а їхні аплікати позначимо відповідно
через
![]() і
і
![]() .
Тоді
.
Тоді
![]() ,
,
![]() і для будь-якої неперервної в області
G
функції
і для будь-якої неперервної в області
G
функції
![]() має місце
формула
має місце
формула
![]()
Зміст
формули (5) такий. Щоб обчислити потрійний
інтеграл, потрібно спочатку обчислити
інтеграл
![]() за змінною Z,
вважаючи X
та Y
сталими. Нижньою
межею цього інтеграла є апліката точки
M
входу
,
а верхньою –
апліката
точки
виходу N.
Внаслідок
інтегрування отримаємо функцію I(x,y)
від змінних x
та y
за змінною Z,
вважаючи X
та Y
сталими. Нижньою
межею цього інтеграла є апліката точки
M
входу
,
а верхньою –
апліката
точки
виходу N.
Внаслідок
інтегрування отримаємо функцію I(x,y)
від змінних x
та y
Якщо
область D,
наприклад,
обмежена кривими
![]() і
і
![]()
![]() ,
де
,
де
![]() і
і
![]() – неперервні функції, тобто
– неперервні функції, тобто
![]() ,
то, переходячи від подвійного інтеграла
,
то, переходячи від подвійного інтеграла
![]() до повторного (п. 1.3), отримаємо формулу
до повторного (п. 1.3), отримаємо формулу
![]() ,(6)
,(6)
яка зводить обчислення потрійного інтеграла до послідовного обчислення трьох визначених інтегралів. Порядок інтегрування може бути й іншим, тобто змінні x,y і z у правій частині формули (6) за певних умов можна міняти місцями. Якщо, наприклад, область G правильна в напрямі осі Ox:
![]() ,
,
де
![]() – неперервні функції, то
– неперервні функції, то
![]() .
.
Зокрема,
якщо областю інтегрування є паралелепіпед:
![]() ,
,
то![]() .
(7)
.
(7)
У
цьому разі інтегрування виконується в
будь-якому порядку, оскільки область G
правильна у напрямі всіх трьох координатних
осей
![]() .
.
Потрійний інтеграл у циліндричних і сферичних координатах.
Як відомо, прямокутні координати через циліндричні можна виразити формулами

Я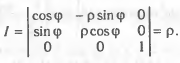 кщо
взяти
кщо
взяти
![]() то
то
![]()
Тоді

Сферичними
координатами
точки
![]() простору
простору
![]() називається трійка чисел
називається трійка чисел
![]() ,
де
,
де
![]() -
довжина радіус-вектора точки
-
довжина радіус-вектора точки
![]() ,
,
![]() - кут, утворений проекцією радіус-вектора
- кут, утворений проекцією радіус-вектора
![]() на площину
на площину
![]() і віссю
і віссю
![]() ,
,
![]() - кут відхилення радіус-вектора
від
осі
- кут відхилення радіус-вектора
від
осі
![]() (див.
рис. 17).
(див.
рис. 17).
Сферичні
координати
пов'язані з декартовими координатами
![]() співвідношеннями:
співвідношеннями:
![]() ,
,
![]() ,
,
![]() (
(![]() ,
,
![]() ,
,
![]() ).
).
Застосування потрійного інтеграла до задач геометрії.
Об’єм тіла
Об’єм
області V
виражається
![]() або формулою
або формулою
![]() -
у декартових координатах,
-
у декартових координатах,
![]() -
у циліндричних координатах,
-
у циліндричних координатах,
![]() -
у сферичних координатах.
-
у сферичних координатах.
Маса тіла
Маса
тіла m
при заданій об'ємній густині
![]() обчислюється за допомогою потрійного
інтеграла
обчислюється за допомогою потрійного
інтеграла
![]() ,
,
де
![]() -
об'ємна густина розподілу маси в точці
-
об'ємна густина розподілу маси в точці
![]() .
.
Застосування потрійного інтеграла до задач механіки і фізики.
Статичні моменти
Моменти
![]() ,
,
![]() ,
,
![]() тіла щодо координатних площин
,
тіла щодо координатних площин
,
![]() ,
,
![]() обчислюються по формулах
обчислюються по формулах
![]() ,
,
![]() ,
,
![]() .
.
Центр ваги тіла
Координати
центра ваги тіла
![]() знаходяться по формулах
знаходяться по формулах
![]() ,
, ![]() ,
, ![]() .
.
Моменти інерції тіла
Моменти інерції тіла щодо координатних площин обчислюються по формулах
![]() ,
,
![]() ,
,
![]() ,
,
а моменти інерції щодо координатних осей:
![]() ,
,
![]() ,
,
![]() .
.
Приклад
2.4.
Знайти
об’єм тіла, обмеженого поверхнями
![]() і
і
![]() .
.
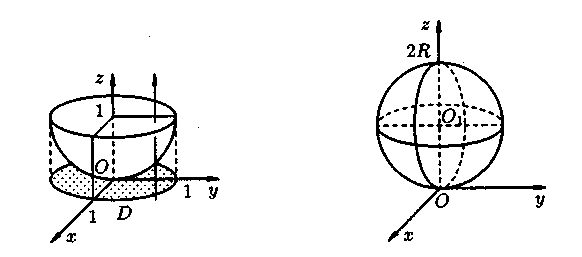
![]() ,
знизу – параболоїдом
(див.
рис. 18). Об’єм тіла знаходимо, використовуючи
циліндричні координати:
,
знизу – параболоїдом
(див.
рис. 18). Об’єм тіла знаходимо, використовуючи
циліндричні координати:
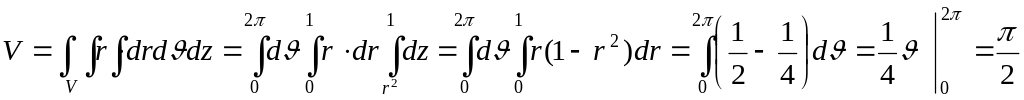 ●
●
