6) Затухающие колебания в среде с вязким трением. Логарифмический декремент, добротность.

В среде с вязким трением при движении пружинного маятника кроме сил тяжести и упругости, действует сила трения, величина которой пропорциональна скорости: F_тр = rv. (Здесь r - коэффициент сопротивления; измеряется в кг/с). Поэтому дифференциальное уравнение принимает вид: где  = r/(2m) - коэффициент затухания; измеряется в с^-1. Известно из практики, что амплитуда затухающих колебаний должна убывать и что благодаря трению колебательный процесс будет "тормозиться", т.е. время одного колебания будет больше. Будем поэтому искать решение в виде где функцию A(t) и "новую" частоту  еще предстоит определить. Дифференцируя, получим и . Подставляя в, получим Уравнение типа выполняется для любого значения t только, если M 0 и N 0. Приравнивая нулю коэффициенты при сos и sin, получим систему дифференциальных уравнений

в торое из которых дает . Чтобы найти константу С, нужно задать начальные условия. Будем считать, что при t=0 . Тогда . Получим

и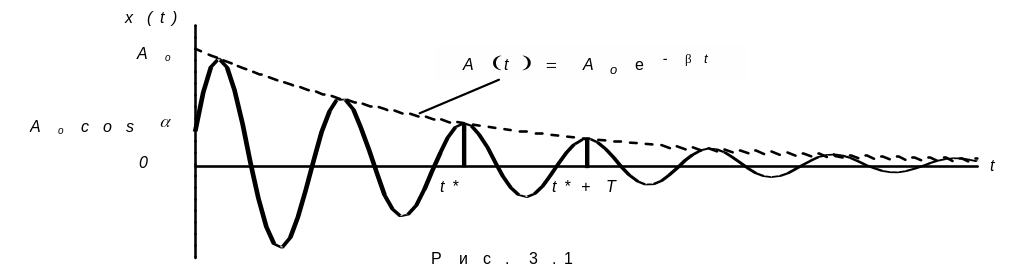 окончательно Осталось найти частоту . Для этого вычислим производные и подставим их в первое уравнение. Получим , откуда Это частота затухающих колебаний. Как видно, предполагаемая "колебательная" форма решения имеет смысл лишь при _o > . Подставляя соотношения, получим решение в виде

.

Логарифм этого отношения называется логарифмическим декрементом затухания:

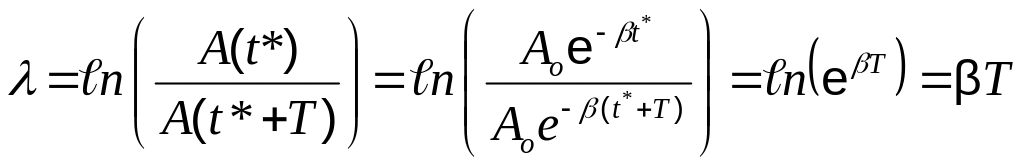
Если отклонения разделены не одним, а N периодами, то нетрудно видеть, что . Если выражение в скобках равно числу "е", то  = 1/N_e , то есть логарифмический декремент - это число, обратное количеству колебаний, по прошествии которых амплитуда уменьшится в е раз. Это произойдет через время  = 1/, которое называется временем релаксации. Поскольку полная энергия Е пропорциональна квадрату амплитуды, то , а величина скорости убывания энергии равна , и если за условный период Т энергия меняется мало, то последнее соотношение можно записать как , где Е - убыль энергии за период. Добротность – мера, характеризующая сохранение энергии в системе. Добротностью колебательной системы называется величина Q, определяемая следующим Аобразом:

.Из определения логарифмического декремента  следует, что для  << 1 добротность .

7) Затухающие колебания в среде с вязким трением. Апериодический и переходные режимы.

А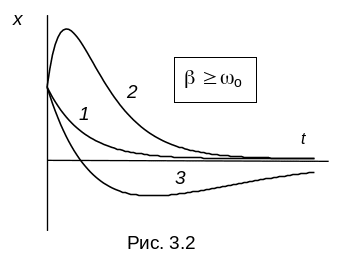 периодический режим – процесс при котором тело без колебательного процесса идет к положению равновесия. Нулевое положение называется устойчивым узлом. При равенстве _о =  решение будет иным (переходный режим):

.

8)Сложение коллинеарных колебаний одинаковых частот. Биения, частота и период биений.

С ложение коллинеарных колебаний (т.е. однонаправленных) можно проиллюстрировать демонстрацией поведения двух маятников, связанных пружиной, или картинкой на экране осциллографа, на вход Y которого подаются гармонические колебания одновременно с двух генераторов. Рассмотрим случай, когда складываются колебания одинаковых частот w₁ = w₂ = w с амплитудами А₁ и А₂­. Это все равно, что две струны, настроенные в унисон. Известно, что в этом случае результатом будет усиленный звук некоторой амплитуды А той же частоты. Новая амплитуда А и новая начальная фаза a: Возводя каждое из них в квадрат и складывая, получим Поделив ,получим для новой начальной фазы: