Колебания.

1. Определение колебательного процесса. Условие периодичности. Гармонические колебания. Амплитуда, частота, период, начальная фаза.

К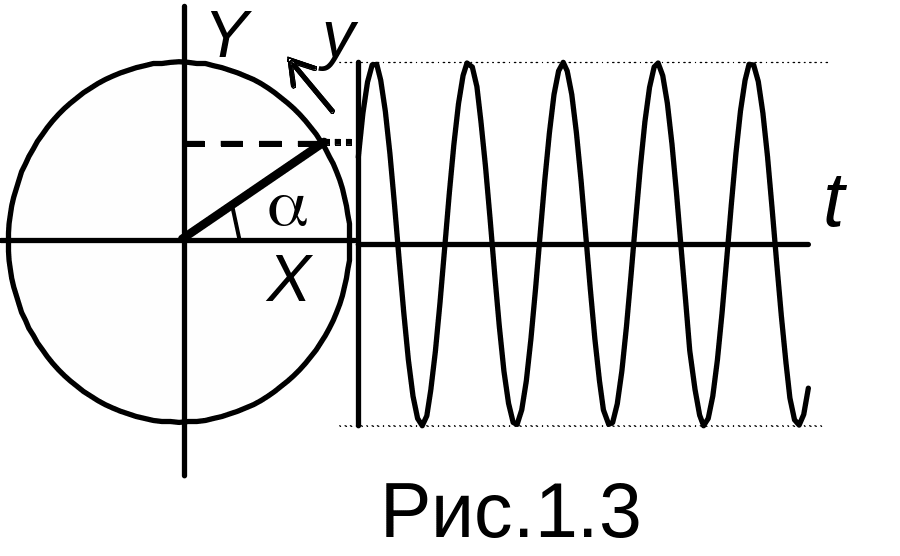 олебательными процессами или просто колебаниями называются процессы, характеризующиеся той или иной степенью повторяемости. Зависимость колеблющейся величины от времени называется временнόй диаграммой. Процесс, повторяющийся в точности спустя определённый один и тот же промежуток времени, называется периодическим, а время, через которое процесс повторяется, называется периодом - Т. Условие периодичности имеет вид х(t) = х(t+T). Число колебаний за единицу времени называется частотой . И если за 1 с происходит  колебаний, а за Т секунд - 1 колебание, то очевидно  = 1/Т. Размерность этой величины []= c^-1. Эта единица называется Герцем (Гц). Гармонические колебания по своей распространенности и значимости занимают особое место. Рассмотрим классический пример таких колебаний, который однако не является определением, а лишь частным случаем. Пусть имеется стержень длиной А, вращающийся с угловой скоростью  против часовой стрелки. В начальный момент (t = 0), изображенный на рисунке, стержень образует угол  с осью Х, а значения его проекций на оси X и Y соответственно равны x(0)=Acos и y(0)=Asin. За следующие t секунд угол увеличится на величину t . Поэтому в любой момент времени значения проекций равны x(t) = A cos (t+) и y(t)=A sin (t+). Гармоническим колебанием называется процесс, при котором значение некоторой переменной величины x(t) изменяется по закону косинуса или синуса: Это - незатухающие колебания, и колебаться по такому закону могут не только значения проекций вращающегося стержня, но и многие куда как более важные физические величины. Тем не менее, рассмотренный пример лежит в основе векторных диаграмм, при помощи которых бывает удобно представить колебание любой физической величины. В параметры А,  и  - константы. Так как sin и cos не могут превышать единицу, то А есть максимальное отклонение колеблющейся величины от положения равновесия - амплитуда. Ее принято считать положительной. Она измеряется в тех же единицах, что и колеблющаяся величина. Понятие амплитуды, строго говоря, применимо только к гармоническому колебанию. Величина , называемая круговой или циклической частотой, как нетрудно видеть, пропорциональна частоте . В самом деле, один полный оборот стержня соответствует углу в 2 радиан: Т=2, откуда =2/Т = 2. Величина (t + ) называется фазой, а ее значение при t = 0 (т.е. ) - начальной фазой колебания. Фаза является углом только, если гармоническое колебание представляется в виде вращающегося вектора. В общем случае это - аргумент косинуса или синуса в законе гармонического колебания и никаким углом не является. Когда в прикладных инженерных расчетах фазу выражают в градусах, то имеют в виду векторную диаграмму, рассмотренную выше.

2)Гармонический осциллятор. Дифференциальное уравнение гармонических колебаний пружинного маятника. Частота, период.

Л юбая система, совершающая такие колебания, называется гармоническим осциллятором. Пружинный маятник представляет собой груз массой m, подвешенный на пружине жесткостью k и совершающий вертикальные колебания. Примем равновесное положение за нулевое и будем считать отклонение груза вниз положительным, а вверх отрицательным. В равновесном положении mg - kx_o = 0, где x_o - начальное удлинение пружины под действием силы тяжести груза. При смещении груза на некоторую величину х возникает возвращающая сила, равная -kx. При этом минус означает, что смещение груза в положительном направлении оси Х приводит к возникновению возвращающей силы kx, направленной в противоположную сторону. Таким образом, по второму закону Ньютон где введены обозначения. Если подставить x(t)=Aco (_Оt +) или х(t)=Asin(_Оt+), то нетрудно видеть, что уравнение удовлетворится при любых А и , и таким образом гармоническое колебание является решением уравнения , которое называется дифференциальным уравнением свободных незатухающих гармонических колебаний. Вообще свободными называются колебания, которые совершает система, однажды выведенная из состояния равновесия и предоставленная самой себе. С математической точки зрения A и  - произвольные константы. Однако задание начальных условий позволяет их однозначно определить. Пусть в нашей задаче заданы начальное смещение и начальная скорость: . Так как ,то Выражая из двух последних соотношений sin и cos, и далее, возводя в квадрат и складывая, получим 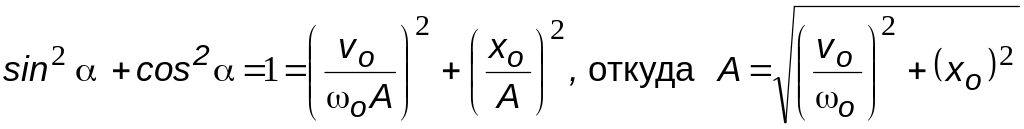Деля эти соотношения друг на друга, найдем . Таким образом, задание двух начальных условий однозначно определяет амплитуду и начальную фазу колебаний. Это означает, что А и  зависят от того, на сколько оттянуть груз и как его толкнуть в начальный момент. Однако от этого не зависит величина - циклическая частота или же - период колебаний пружинного маятника.