Лекция №5. Атмосферное давление и плотность воздуха.

УДК 551.46+551.5(075.3) Кузнецов Ю.М. к.т.н., доцент

кафедры «Судовождения»

План

1. Атмосферное давление, единицы измерения.

2. Основные уравнения статики.

3. Приведение давления к уровню моря.

4. Барические системы.

5. Барическая ступень.

6. Карты барической топографии.

7. Плотность воздуха.

8. Измерения атмосферного давления.

5.1. Атмосферное давление.

Давление воздуха – это сила, с которой атмосфера давит на единичную площадку. В каждой точке воздушного пространства оно равно весу вышележащего столба воздуха поперечным сечением 1 см² и высотой от данного уровня до верхней границы атмосферы. Давление быстро убывает с высотой: на высоте 5,5 км оно в среднем равно половине приземного давления, а на высоте 50 км – одной тысячной.

За нормальное атмосферное давление принимают давление, которое уравновешивается весом ртутного столба высотой 760 мм с основанием 1 см² при температуре 0° на широте 45° и на уровне моря, где ускорение свободного падения g_° = 980,665 см/с².

В метеорологии пользуются не условными единицами давления (мм рт.ст.), а абсолютными – миллибарами (мбар). Между ними существует следующая связь

1 мм рт.ст. = 1,33 мбар

1 мбар 0,75 мм рт.ст.

760 мм рт.ст. = 1013,25 мбар

В международной системе единиц (СИ) за единицу давления принят паскаль (Па) – это давление, вызываемое силой в 1 Н на поверхность площадью 1 м².

1 мбар = 100 Па

760 мбар = 1013,25 гектопаскаль

5.2. Основное уравнение статики

Атмосфера находится в постоянном движении по отношению к земной поверхности, состояние покоя наблюдается редко, лишь в том случае, когда горизонтальная составляющая градиента давления равна нулю, а вертикальная составляющая градиента давления уравновешивается силой тяжести воздуха

Р = ρgdz × 1 см² (5.1)

Уравнение, описывающее изменение атмосферного давления dP с высотой dz в предположении статического равновесия, называется уравнением статики атмосферы

– = ρg (5.2)

или dP = – ρgdz (5.3)

где – – вертикальная составляющая градиента давления;

ρ – плотность воздуха;

g – ускорение свободного падения.

Из уравнения (5.2) можно сделать следующие важные выводы:

a) В атмосфере давление всегда падает с увеличением высоты, т.е. dP < 0, т.к. в правой части уравнения произведение состоит только из положительных множителей (ρgdz > 0).

б) Атмосферное давление на каждом уровне представляет собой вес столба воздуха с поперечным сечением 1 см² высотой от данного уровня до верхней границы атмосферы.

Действительно, проигнорировав уравнение (5.2) в пределах от Z, где давление равно P, до Z_a, где давление равно нулю (на верхней границе), получим

⁼ или P = ρg(Z_a – Z) (5.4)

в) Чем выше расположен уровень, тем меньше величина падения давления при подъеме на одну и ту же высоту. Это объясняется тем, что входящая в уровнение статики (5.3) плотность ρ убывает с увеличением высоты, поэтому уменьшается и величина dP.

Основное уровнение статики атмосферы, вычисленное при различных условиях, даёт ряд так называемых барометрических формул (Табл.5.1)

Табл.5.1

Основные барометрические формулы

Атмосфера и её начальные условия	Барометрические формулы
-однородная (гидросфера Земли) (ρ= ρ0=const g=g0=const)	P= P0- ρgz
-изометрическая (T=T0=const, g=g0=const, воздух сухой)	ln P=ln P0- gz/(RcT0) или P=P0× e-gz/(RcT0) Rc-газовая постоянная сухого воздуха
- политропная (T=T0-γz, g=g0=const, воздух сухой)	= γ-вертикальный градиент температуры

Из приведенных в таблице формул следует:

1. Давление воздуха в однородной атмосфере падает с высотой по линейному закону.

2. Давление воздуха в изотермической атмосфере убывает с высотой по экспоненте. Отсюда вытекает следующие закономерности:

- если высота растет в прогрессии арифметической, то давление убывает в геометрической прогрессии;

- при более высокой температуре давление в изотермической атмосфере падает с высотой медленнее, чем при более низкой;

- чем выше расположен слой атмосферы определенной толщины, тем меньше величина падения давления в этом слое.

3. Давление воздуха в политропной атмосфере при большем значении вертикального градиента температуры γ падает с высоты быстрее, чем при меньшем значении градиента.

Барометрические формулы дают возможность решать следующие задачи:

- определять превышение z одного уровня над другим, если известны P₀,t₀,P_z,t_z (барометрическое нивелирование);

- определять давление P₀ на нижнем уровне, если известны Z,P_z,t_z (приведение давления, например, к уровню моря, взлетно-посадочной полосе (ВПП));

- определять давление на какой-либо высоте, если известны P₀,t₀, z.

Для решения перечисленных задач наибольшее применение получила формула Лапласа

H=18400(I + t_cp) lg (5.5)

Где H- толщина слоя в метрах;

t_cp- средняя температура слоя;

P_1,P₂- давление на нижней и верхней границе слоя;

=0,004

Необходимость приведения давления к уровню моря диктуется следующим:

Метеорологические станции, на которых производится измерение давления и других метеорологических элементов, расположены на различной высоте над уровнем моря. Так как давление изменяется с высотой, то измеренные на станциях значения его будут различаться прежде всего под влиянием разности высот. Оценить изменение давления в горизонтальном направлении ( в частности, рассчитать горизонтальный градиент давления) можно, очевидно, только тогда, когда давление приведено к какому-либо одному уровню. В качестве такого уровня выбирается обычно уровень моря.

Для этого надо знать: высоту метеостанции над уровнем моря, давление на уровне метеостанции, среднюю температуру воздуха между уровнем моря и метеостанцией.

Приведение давлений производится наблюдателем метеостанции с помощью заранее вычисленных по барометрической формуле таблиц.

Приведенное к уровню моря давление вместе с другими метеоэлементами (температура, точка росы, скорость ветра, количество высоты и форма облачности) наносятся на так называемые синоптические приземные карты (рис.5.1), речь о которых пойдет ниже.

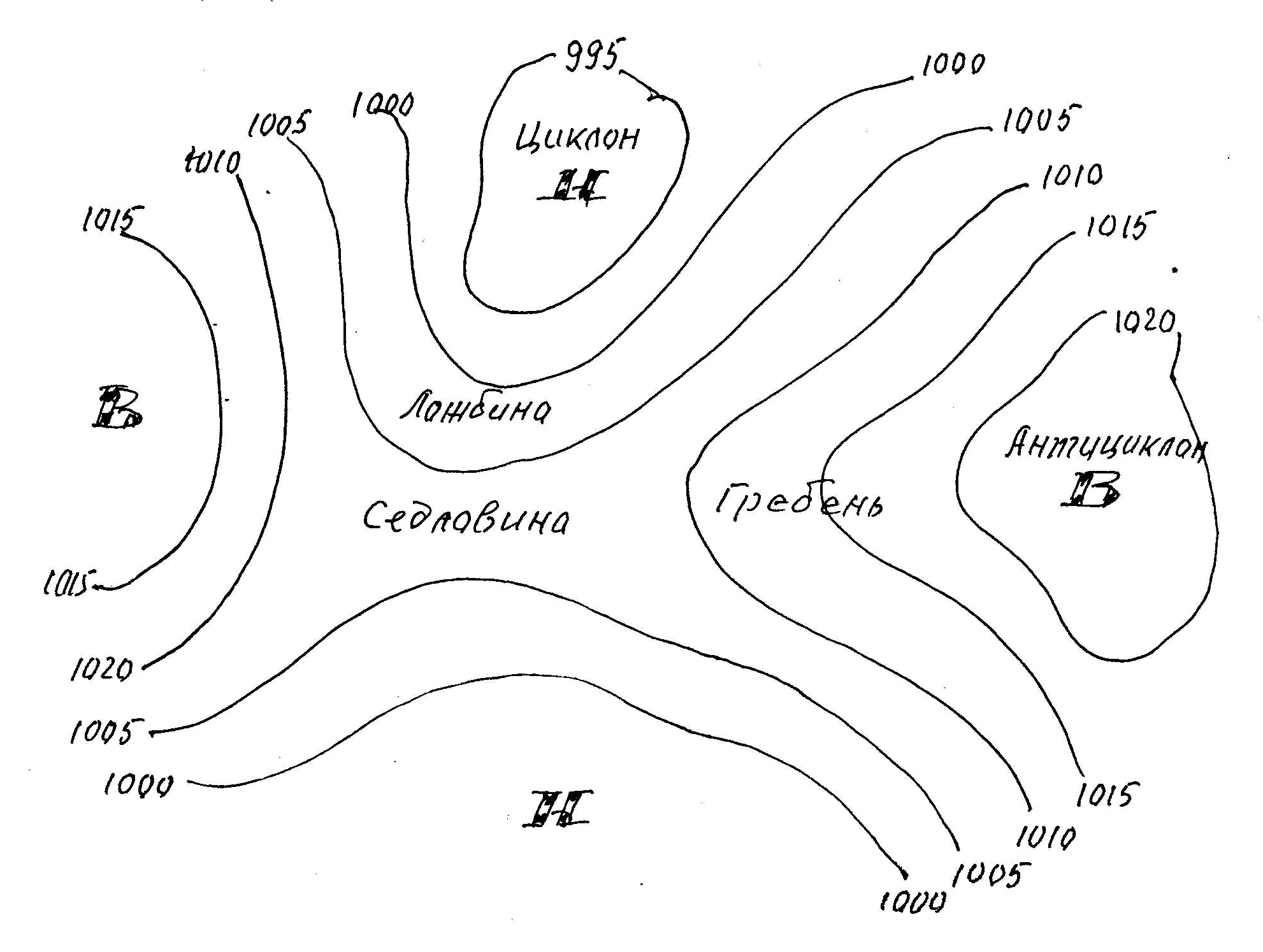
Рис.5.1. Основные барические системы

На борт самолетов для обеспеченности их посадки передается значение атмосферного давления (в мм рт.ст.), приведенное к уровню ВПП.

Для ориентировочной оценки изменения давления с высотой, а также приближенного расчета изменения высоты по разности давлений на практике удобно пользоваться барической ступенью.

Барическая ступень- это такая высота, на которую нужно подняться или опустится, чтобы давление изменилось на единицу (1 мб или 1 мм рт. ст.).

Расчет барической ступени производится по формуле

h= (1 + t ) (5.6)

где P- давление, t- температура, =0,004.

Из формулы следует, что

-в теплом воздухе барическая ступень больше, чем в холодном;

-с высотой барическая ступень возрастает, так как она обратно пропорциональна давлению воздуха;

-чем меньше барическая ступень, тем быстрее давление падает с высотой (табл.5.2)

Таблица 5.2 - Изменение барической ступени в зависимости от давления и температуры воздуха (м/мбар)

Давление,мбар	Температура, °С
	- 40	- 20	0	20	40
1000	6,7	7,4	8,0	8,6	9,3
500	13,4	14,7	16,0	17,3	18,8
100	67,2	73,6	80,0	86,4	92,6

Как видно из таблицы, ошибка при отсчете и передачи на борт самолета приведенного к уровню ВПП давления в 1 мбар при температуре 20°С приведет к ошибке в высоте пилотирования над точкой приземления

∆Z=1мбар×0,75×8,6=6,4 м,

что в условиях плохой видимости чревато опасными последствиями.

Для анализа полей давления в свободной атмосфере широкое применение получил метод барической топографии (БТ), в основе которого лежат карты БТ, составляемые на основе данных зондирования атмосферы во многих точках Земли.

На них вместо давления наносится высота поверхности с равным давлением (например, 850, 700, 500, мб и т.д.), измеряемая в геопотенциальных метрах.

Геопотенциалом Ф точки называется работа, которую необходимо совершить, чтобы поднять единицу массы в поле силы тяжести от центра Земли до заданного уровня. Условились геопотенциал на уровне моря считать равным 0.

Для вычисления абсолютных высот изобарических поверхностей используют формулу

Ф_р= 67,4 T₀ lg гп. м (5.7)

где T₀- виртуальная температура,

P₀- давление на уровне моря,

Р- давление на западном уровне (изобарическая поверхность).

Карты с нанесением на них значениями абсолютной высоты изобарической поверхности называют картами абсолютной топографии (АТ). На таких картах линии равных значений Ф_р проводятся через 40 гп.м (4 д.гп.м) и называются изогипсами.

Широкое применение получила также карта относительной топографии (ОТ), на которые наносятся значения относительных высот, т.е. превышение одной изобарической поверхности над другой.

Расчетная формула имеет вид

=67,4 T₀ lg (5.8)

Относительная высота зависит только от средней температуры столба воздуха, заключенного между изобарическими поверхностями.