1. Рівномірний з параметрами

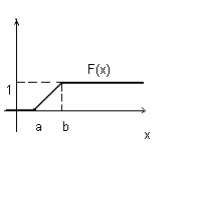
F(x) - кусково-диференційовна

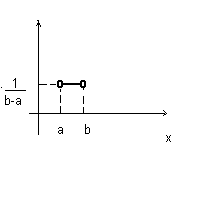
2. Показниковий з параметром

3. Нормальний з параметрами

,

Стандартний гауссівський розподіл - N(0,1):

,

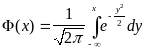
5.Центральна гранична теорема 1

для однаково розподілених незалежних випадкових величин

Теорема. Якщо випадкові величини є незалежними та однаково розподіленими і мають математичне сподівання , та скінчену дисперсію , тоді

=

тобто збігається до функції розподілу нормального закону.

Рівномірна збіжніть є наслідком слабкої збіжності та неперервності нормального розподілу. Позначимо і запишемо характеристичну функцію

- потрібно показати, що вона збігається до х.ф. нормального розподілу. Можна вважати, що а = 0 інакше можна було б розглянути - нові в.в. з мат. сподіванням, рівним 0, та .

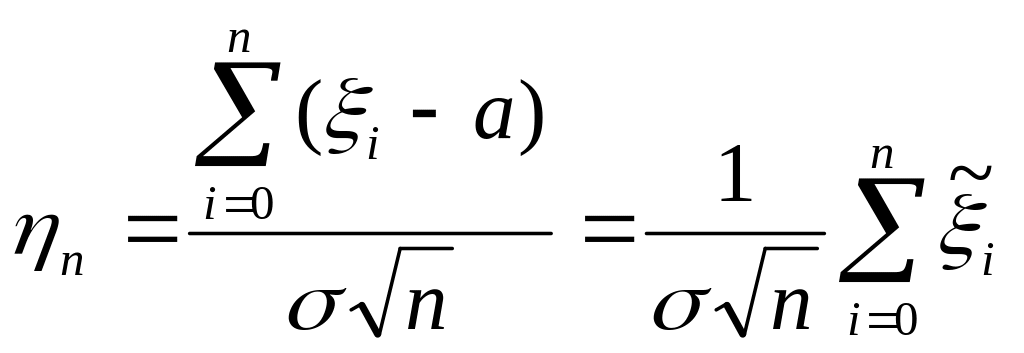Враховуючи, що

, . Оскільки існує , то справедливий розклад . Крім того

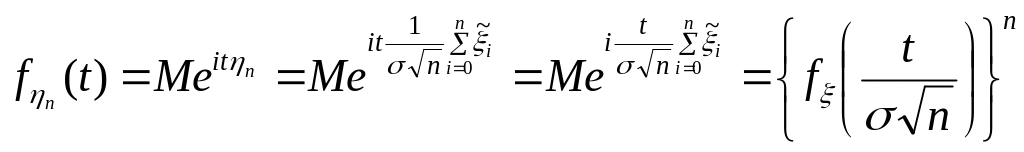
Остаточно 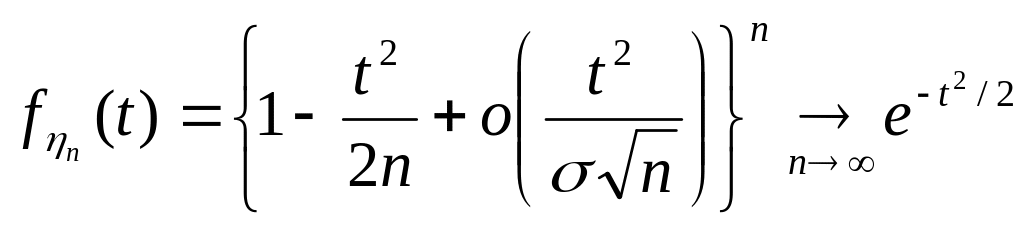, що і т.д.

Наслідок (Інтегральна теорема Муавра-Лапласа)

Теорема Якщо задана схема випробувань Бернуллі, а - число успіхів у серії з n випробувань, то - р ймовірність успіху

Розглянемо множину кожна з яких має розподіл Бернуллі, тобто

, , .



6. Поняття випадкового процесу. Вінерівський та пуасонівський процеси.

Озн. Випадковий процес - це система в.в. , , - проміжок часу, яка описує еволюцію процесу, що досліджується, - значення характеристики, що досліджується, в момент

У ТЙ:

ВП - множина в.в. , визначена на одному і тому ж імовірністному просторі . інтерпретується як час.

Класифікація ВП:

1. за типом :

а) - дискретна, - процеси з дискретним часом.

У цьому випадку ВП - це послідовність в.в.

б) - процеси з неперервним часом.

2. За типом множини значень:

- дискретні - процеси з дискретним часом

- неперервні - процеси з неперервним часом

3. За способом опису спільних розподілів

Множину значень називають також множиною можливих станів.

- поле

Озн. 1)Процесом з незалежними приростами називається випадковий процес, визначенийй для із дискретною або неперервною множиною станів, для якого виконується умова: для будь-якого скінченого набору моментів часу випадкові величини - незалежні.

2. Однорідні ПНП - це процеси, у яких:

а) ;

б) розподіл залежить тільки від , тобто співпадає з розподілом .

3. Стохастично-неперервні ОПНП - це такі, у яких 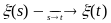, тобто

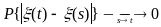
Характеристична функція для с/н ОПНП

Із властивостей характеристичних функцій випливає, що

, .

Теорема Характеристична функція с/н ОПНП представляється у вигляді , де - кумулянта процесу.

Висновок: для задання с/н ОПНП необхідно і достатньо задати кумулянту

Теорема. (Про представлення кумулянти)

Кумулянта представляється у вигляді:

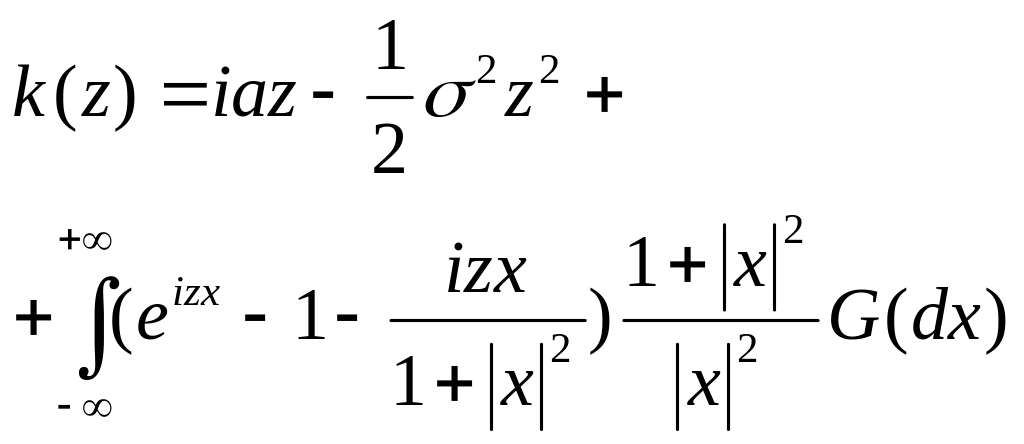, де , - скінчена міра, що не має атома в нулі: .

Вінерівський процес.

, тобто . Позначається .

В цьому випадку процес можна вибрати так, що траєкторії процесу, тобто є для фіксованих неперервними.

Отже, - це с/н ОПНП, , з неперервними траєкторіями, і характеризується нормальним розподілом

Пуасонівський процес

1. 

-пуасонівська в.в.

Пуасонівським процесом називається однорідний процес з незалежними приростами, що дорівнює 0 в 0, у якого розподіл процесу в момент є пуасонівською випадковою величиною із параметром .

2. Друга характеризація ПП.

а) - кількість подій до моменту

- не залежить від приростів на будь-яких інших інтервалахі, які не перетинаються з

б) залежить тільки від (однорідність)

в) в кожний момент часу відбувається тільки одна подія потоку (ординарність)

Поток подій, який характеризується цими властивостями є найпростішим, а отже є процесом чистого росту чи пуасонівським