
- •Теорія ймовірностей
- •1. Аксіоматичне означення ймовірності. Формула повної імовірності та ф-ла Баєса.
- •2. Випадкові величини. Властивості функцій розподілу.
- •3.Нерівність Чебишева. Закон великих чисел
- •4. Основні типи дискретних та неперервних розподілів.
- •1. Рівномірний з параметрами
- •2. Показниковий з параметром
- •3. Нормальний з параметрами
- •5.Центральна гранична теорема 1
- •6. Поняття випадкового процесу. Вінерівський та пуасонівський процеси.
- •7. Випадкове середнє та дисперсія. Емпірична функція розподілу. Теореми глівенка та колмогорова
- •8.Перевірка статистичних гіпотез. Критерії згоди колмогорова і 2 ( критерій пірсона).
1. Аксіоматичне означення ймовірності. Формула повної імовірності та ф-ла Баєса. 2
2. Випадкові величини. Властивості функцій розподілу. 3
3.Нерівність Чебишева. Закон великих чисел 4
4. Основні типи дискретних та неперервних розподілів. 5
5.Центральна гранична теорема 1 7
для однаково розподілених незалежних випадкових величин 7
6. ПОНЯТТЯ ВИПАДКОВОГО ПРОЦЕСУ. ВІНЕРІВСЬКИЙ ТА ПУАСОНІВСЬКИЙ ПРОЦЕСИ. 8
7. ВИПАДКОВЕ СЕРЕДНЄ ТА ДИСПЕРСІЯ. ЕМПІРИЧНА ФУНКЦІЯ РОЗПОДІЛУ. ТЕОРЕМИ ГЛІВЕНКА ТА КОЛМОГОРОВА 9
8.ПЕРЕВІРКА СТАТИСТИЧНИХ ГІПОТЕЗ. КРИТЕРІЇ ЗГОДИ КОЛМОГОРОВА І 2 ( КРИТЕРІЙ ПІРСОНА). 10
Теорія ймовірностей
1. Аксіоматичне означення ймовірності. Формула повної імовірності та ф-ла Баєса.
Спочату введемо кілька допоміжних понять.
Озн. Множина U є алгеброю, якщо
1)
![]()
2)
![]() і
і
![]()
3).
![]()
Озн.
Множина U є
![]() -алгеброю,
якщо
-алгеброю,
якщо
1)
2)![]() і
і
![]()
3).
Будемо вважати, що множина всіх подій утворює -алгебру.
Озн. Числову функцію, задану на множині всіх подій U, будемо називати ймовірністю, якщо
Р(А)
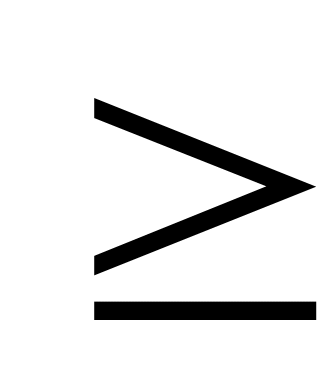 0;
0;Р(
 )=1;
Р(
)=1;
Р( )=0;
)=0;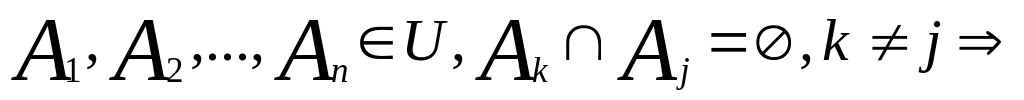
 .
.
Озн.
Ймовірносний простір- це трійка об
єктів: (![]() ).
).
Озн. Під аксіоматикою теорії ймовірності розуміють три властивості, накладені на U, і три властивості накладені на Р.
Відомо ряд важливих наслідків з цих властивостей, які легко доводяться. Приведемо їх.
1.
Якщо![]() , то
, то
![]() .
.
2.
![]() .
.
3.
P(![]() )=
0.
)=
0.
4.
P(![]() )=P(A)+P(B)-P(
)=P(A)+P(B)-P(![]() ),
),![]()
![]() .
.
5. Неперервність зверху:
![]() і
і
![]() =
,
тоді має місце
=
,
тоді має місце
![]() .
.
Озн.
Умовною ймовірністю прийнято називати
величину Р(А/В)=![]()
Озн. А і В - незалежні події, якщо Р( )=Р(А)Р(В).
Озн.
Кажуть, що
![]() утв-ють повну групу подій, якщо
утв-ють повну групу подій, якщо
![]() .
.
Формула
повної ймовірності має вигляд, якщо
![]() - повна група подій,
- повна група подій,
![]() .
Дійсно
.
Дійсно

Формула Баєса відповідно має вигляд (при тих же припущеннях)
2. Випадкові величини. Властивості функцій розподілу.
Нехай
маємо ймовірносний простір (![]() ,
F, P).
,
F, P).
![]() -
деяка функція, визначена на
.
-
деяка функція, визначена на
.
Озн. -буде вимірною функцією, якщо
![]() ,
де F
,
де F
![]() алгебра.
алгебра.
Озн.
Вимірна функція
![]() -
випадкова величина ,
-
випадкова величина ,
![]() .
.
Озн.
F(x)=
![]() - функція розподілу випадкової величини
.
- функція розподілу випадкової величини
.
Властивості функцій розподілу.
1. F(x) – невід’ємна
2. F(x) - монотонно неспадна.(x1>=x2 => F(x1)>=F(x2) )Справді:
 Отже
Отже
3. F(x) - неперервна зліва. Тобто F(x-0) = F(x)
4.
Нормованою F(-![]() )
= 0 , F(+
)
= 1.
)
= 0 , F(+
)
= 1.
Дискретні випадкові величини.
Нехай
<
>
ймовірнісний простір. Дискретною
випадковою величиною
називається функція
на ,
яка набуває скінченне
або зліченне
число значень х1,
х2,
…, хn ,
… і є вимірною відносно
алгебри .
Це означає, що для кожного хі
{
:
x}
(1).Дійсно, якщо для функції
має місце співвідношення (1), то ця
функція вимірна відносно ,
так як для кожного дійсного х {
:
x}=
![]() {
:
xі}
.
Крім того, якщо
вимірна відносно
алгебри ,
то за Теоремою 1 для кожного дійсного х
{
:
x
}
.
Таким чином, якщо
дискретна випадкова величина на
ймовірнісному просторі <
>,
яка приймає значення х1,
х2,
…, хn,
…, то для кожного n визначена
ймовірність
Рn=Р{
:
xn}
Нехай ()
– дискретна випадкова величина, яка
набуває значення х1,…,
хі,….
Набір чисел Р{:()=xi}=pi
(i=1,2,…)
називають р
о з п о д і л о м випадкової
величини .
Зрозуміло, що рі
0,
{
:
xі}
.
Крім того, якщо
вимірна відносно
алгебри ,
то за Теоремою 1 для кожного дійсного х
{
:
x
}
.
Таким чином, якщо
дискретна випадкова величина на
ймовірнісному просторі <
>,
яка приймає значення х1,
х2,
…, хn,
…, то для кожного n визначена
ймовірність
Рn=Р{
:
xn}
Нехай ()
– дискретна випадкова величина, яка
набуває значення х1,…,
хі,….
Набір чисел Р{:()=xi}=pi
(i=1,2,…)
називають р
о з п о д і л о м випадкової
величини .
Зрозуміло, що рі
0,
![]() .
.
Функція розподілу дискретної випадкової величини () визначається рівністю
![]()
Сумісний розподіл випадкових величин () і (). Нехай () – дискретна випадкова величина, яка набуває значень х1, х2,…, хі,…, () – дискретна випадкова величина, яка набуває значень y1, y2,…, yі,…. Набір чисел Р{:()=xi, ()=yi}=pij (i=1, 2, …; j=1, 2, …) називається сумісним розподілом випадкових величин і (розподілом випадкового вектора (, )). Мають місце такі твердження:
а)
рij0,
![]()
б)
![]() де {pi}
розподіл (),
{qi} –
розподіл ().
де {pi}
розподіл (),
{qi} –
розподіл ().
Незалежні випадкові величини. Випадкові величини і н а з и в а ю т ь с я н е з а л е ж н и м и, якщо для будь-яких i j
P{()=xi, ()= yi} = P{()=xi} P{()= yi}.
Математичне сподівання випадкової величини. Нехай () – дискретна випадкова величина, яка набуває значень хі з імовірностями рі(і=1, 2, …). Припустимо, що ряд хірі збігається. Тоді м а т е м а т и ч н и м с п оді-
в
а н н я м випадкової величини ()
називається сума ряду М ()
=
![]() Якщо
хірі=+,
то кажуть, що випадкова величина ()
не має математичного сподівання.
Математичне сподівання суми випадкових
величин дорівнює сумі математичних
сподівань.
Якщо
хірі=+,
то кажуть, що випадкова величина ()
не має математичного сподівання.
Математичне сподівання суми випадкових
величин дорівнює сумі математичних
сподівань.
Дисперсія випадкової величини () визначається рівністю
D=M[-
M]2=
M2-(
M)2=![]()
Властивості дисперсії.
D=0
 =соnst;
=соnst;D=

D(C)=c2 D;
D(
 C)=
D
.
C)=
D
.Якщо
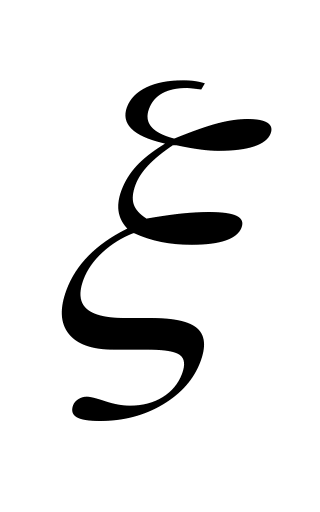 та
та
 незалежні випадкові
величини, то D(
)=
D
+D
.
незалежні випадкові
величини, то D(
)=
D
+D
.
Коєфіцієнт коваріації випадкових величин та це: cov(, )=M(-M)(-M).
Коефіцієнт кореляції. К о є ф і ц і є н т о м к о р е л я ц і ї випадкових величин і називаються
![]()
Мають місце такі твердження:
а) r(, ) 1;
б) якщо і незалежні, то r(, )=0;
в) якщо r(, )=1, то з імовірністю одиниця =а+b, де а і b – деякі сталі.
