Задача 1.
Найти
значения переменных
,
удовлетворяющие неравенствам:
условиям
не отрицательности
,
и придающие целевой функции (ЦФ)
экстремальные значения (max и min).
Задачу решить графическим методом: построить область решения, градиент ЦФ, линии уровня ЦФ для точек максимума и минимума.
В случае множества оптимальных планов найти общий вид решения. Вычислите максимальное и минимальное значения ЦФ. Записать ответ и сделать проверку.
Решение:
На
координатной плоскости
построим область решений, удовлетворяющих
неравенствам
(область заштрихована):
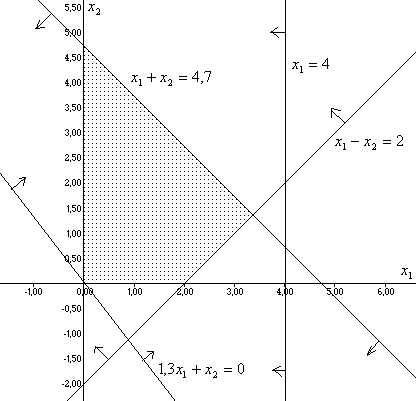
На
построенной области функция
должна принять экстремальные значения.
Построим линию уровня для
,
т.е. прямую
и градиент ЦФ равный вектору
.
Функция
будет возрастать в направлении вектора
и убывать в противоположном направлении.
Сдвигая параллельным переносом прямую
в направлении роста или убывания функции
до касания крайних точек области, мы
получим линии уровня (пунктирные) для
максимального и минимального значений
функции
.
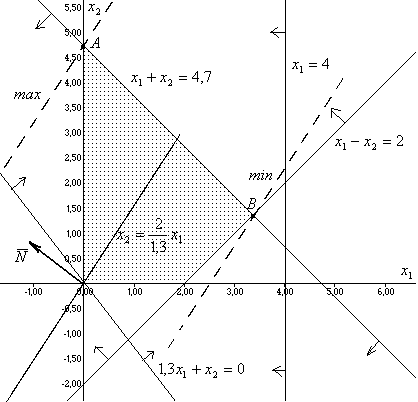
Максимум функция достигнет в точке А, а минимум в точке В. Найдём координаты этих точек.
-
точка А:
,
а
найдём из уравнения
,
т.е.
;
-
точка В: её координаты найдём решив
систему
:
В итоге:
Выполним проверку:
на максимум:
|
на минимум:
|
Ответ:
; 
.
Задача 2.
Найти
значения переменных
,
удовлетворяющие неравенствам:
условиям
не отрицательности
,
и придающие ЦФ
максимальное значение.
Задачу
решить симплекс-методом. Предварительно,
при помощи введения дополнительных не
отрицательных базисных переменных
,
записать задачу в канонической форме.
Решение задачи представить в виде соответствующих симплексных таблиц со столбиками контрольных сумм. Записать ответ и сделать проверку.
Решение:
Решим поставленную задачу симплекс-методом.
Введём дополнительные неотрицательные переменные для получения задачи в канонической форме:
Составим симплекс-таблицу:
базис |
Сбаз |
А0 |
5 |
6 |
8 |
0 |
0 |
0 |
|
|
|
|
|
|
|||
|
0 |
22 |
2 |
1 |
3 |
1 |
0 |
0 |
|
0 |
27 |
1 |
4 |
2 |
0 |
1 |
0 |
|
0 |
23 |
3 |
0 |
2 |
0 |
0 |
1 |
|
|
Z = 0 |
-5 |
-6 |
-8 |
0 |
0 |
0 |
Условием
оптимальности задачи на максимум
является
.
Находим
минимальное
и определяем минимальное положительное
значение
:
базис |
Сбаз |
А0 |
5 |
6 |
8 |
0 |
0 |
0 |
|
|
|
|
|
|
|
||||
|
0 |
22 |
2 |
1 |
3 |
1 |
0 |
0 |
7,333 |
|
0 |
27 |
1 |
4 |
2 |
0 |
1 |
0 |
13,5 |
|
0 |
23 |
3 |
0 |
2 |
0 |
0 |
1 |
11,5 |
|
|
Z = 0 |
-5 |
-6 |
-8 |
0 |
0 |
0 |
|
Выбираем столбец переменных и затем строку базиса .
Произведём замену базисной переменной на переменную и пересчитаем коэффициенты, при необходимости продолжим оптимизацию:
базис |
Сбаз |
А0 |
5 |
6 |
8 |
0 |
0 |
0 |
|
|
|
|
|
|
|
||||
|
8 |
22/3 |
2/3 |
1/3 |
1 |
1/3 |
0 |
0 |
22 |
|
0 |
37/3 |
-1/3 |
10/3 |
0 |
-2/3 |
1 |
0 |
3,7 |
|
0 |
25/3 |
5/3 |
-2/3 |
0 |
-2/3 |
0 |
1 |
- |
|
|
Z = 176/3 |
1/3 |
-10/3 |
0 |
8/3 |
0 |
0 |
|
базис |
Сбаз |
А0 |
5 |
6 |
8 |
0 |
0 |
0 |
|
|
|
|
|
|
|
||||
|
8 |
6,1 |
0,7 |
0 |
1 |
0,4 |
-0,1 |
0 |
|
|
6 |
3,7 |
-0,1 |
1 |
0 |
-0,2 |
0,3 |
0 |
|
|
0 |
10,8 |
1,6 |
0 |
0 |
-0,8 |
0,2 |
1 |
|
|
|
Z = 71 |
0 |
0 |
0 |
2 |
1 |
0 |
|
Получили,
что все
,
т.е. условие оптимальности выполнено.
Решением
является вектор
при этом максимум функции Z
будет равен
или в условиях исходной задачи:
.
Выполним проверку:
Ответ:
.
Задача 3.
Найти значения переменных , удовлетворяющие ограничениям:
условиям не отрицательности ,
и придающие ЦФ
максимальное значение.
Решить
задачу методом искусственного базиса:
сначала записать задачу при помощи
неотрицательных дополнительных
переменных
в канонической форме, затем при помощи
неотрицательных искусственных базисных
переменных
сформулировать соответствующую М-задачу,
которую решить симплекс-методом. Решение
М-задачи представить в виде соответствующих
симплекс-таблиц со столбиком контрольных
сумм.
Записать решение исходной задачи, используя оптимальное решение М-задачи в виде ответа. Сделать проверку исходной задачи.