
О дин из вариантов решения задачи (рисунок обязателен).
Условие механического равновесия проводника приводит к системе уравнений: 2k Δl cos α = mg, 2kΔl sin α = IBL.
Поделим
второе равенство на первое: tg
α
=![]() .
Масса провода m
= ρLS.
Таким образом, tg
α
=
.
Масса провода m
= ρLS.
Таким образом, tg
α
=![]() =
1. Откуда α
= 45°.
=
1. Откуда α
= 45°.
Задача 9. На непроводящей горизонтальной поверхности стола лежит проводящая жёсткая тонкая рамка в виде равностороннего треугольника ADC со стороной, равной а (см. рисунок). Рамка, по которой течет ток I, находится в однородном горизонтальном магнитном поле, вектор индукции которого перпендикулярен стороне CD. Каков должен быть модуль индукции магнитного поля, чтобы рамка начала приподниматься относительно стороны CD, если масса рамки m?
О дин
из вариантов решения задачи. По рамке
течет ток I. Пусть модуль
вектора магнитной индукции равен В. На
стороны рамки действует сила Ампера.
На сторону AC:
FA1=
IaВ
sin(π-
α) =
дин
из вариантов решения задачи. По рамке
течет ток I. Пусть модуль
вектора магнитной индукции равен В. На
стороны рамки действует сила Ампера.
На сторону AC:
FA1=
IaВ
sin(π-
α) =
![]() IaВ.
На сторону AD:
FA2
= IaВ
sinα
=
IaВ.
На сторону CD:
FA3
= IaВ.
Суммарный момент
этих сил относительно оси CD
NA=FA
IaВ.
На сторону AD:
FA2
= IaВ
sinα
=
IaВ.
На сторону CD:
FA3
= IaВ.
Суммарный момент
этих сил относительно оси CD
NA=FA![]() +
FA
=
IaВ
=
+
FA
=
IaВ
=![]() .
Момент силы
тяжести Ng
=
.
Момент силы
тяжести Ng
=![]() .
Условия отрыва
NA
+ Ng
≥ 0,
>
.
.
Условия отрыва
NA
+ Ng
≥ 0,
>
.
Отсюда
В ≥
![]() .
Допускается ответ в виде равенства.
.
Допускается ответ в виде равенства.

Задача 10. На непроводящей горизонтальной поверхности стола лежит проводящая жёсткая рамка из однородной тонкой проволоки, согнутая в виде квадрата ACDE со стороной а (см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции В которого перпендикулярен сторонам АЕ и CD и равен по модулю В. Какой силы ток нужно пропустить по рамке против часовой стрелки, чтобы она начала приподниматься, вращаясь вокруг оси, совпадающей со стороной CD, если масса рамки m?
О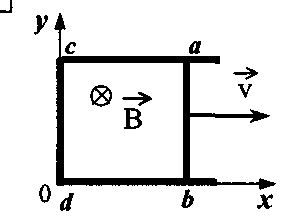 дин
из вариантов решения задачи. Пусть
по рамке течет ток I . На
стороны АЕ и CD будут
действовать силы Ампера FA1=
Fa2
= IaB.
Момент силы Ампера относительно оси,
проходящей через сторону CD,
NA =
Ia2B.
Момент силы тяжести относительно оси
CD Ng
= -
mga.
Условие отрыва NA
≥ Ng,
Ia2B
≥
mga.
Отсюда I ≥
дин
из вариантов решения задачи. Пусть
по рамке течет ток I . На
стороны АЕ и CD будут
действовать силы Ампера FA1=
Fa2
= IaB.
Момент силы Ампера относительно оси,
проходящей через сторону CD,
NA =
Ia2B.
Момент силы тяжести относительно оси
CD Ng
= -
mga.
Условие отрыва NA
≥ Ng,
Ia2B
≥
mga.
Отсюда I ≥
![]() .
Допускается ответ в виде равенства.
.
Допускается ответ в виде равенства.
Задача 11. По П-образному проводнику постоянного сечения со скоростью v скользит проводящая перемычка ab такого же сечения, длиной l. Проводники помещены в постоянное однородное магнитное поле, вектор индукции которого В направлен перпендикулярно плоскости проводников (см. рисунок). Определите напряженность электрического поля Е в перемычке в тот момент, когда ab = ас. Сопротивление между проводниками в точках контакта пренебрежимо мало.
Один
из вариантов решения задачи. При
движении перемычки в магнитном поле в
ней возникает ЭДС индукции
![]() =
B/v. По закону
Ома для замкнутой цепи abcd:
=
B/v. По закону
Ома для замкнутой цепи abcd:
I
=![]() ,
где R - сопротивление
перемычки ab, тогда
выражение для разности потенциалов
между точками а и b
имеет вид: U = I·3R=
,
где R - сопротивление
перемычки ab, тогда
выражение для разности потенциалов
между точками а и b
имеет вид: U = I·3R=![]() Blv.
Так как Е =U/l,
то Е =
Bv.
Blv.
Так как Е =U/l,
то Е =
Bv.
Задача
12. Г оризонтально
расположенный проводник длиной 1 м
движется равноускоренно в вертикальном
однородном магнитном поле, индукция
которого направлена перпендикулярно
проводнику и скорости его движения (см.
рисунок). При начальной скорости
проводника, равной нулю, и ускорении
8 м/с2, он переместился
на 1 м. Какова индукция магнитного
поля, в котором двигался проводник, если
ЭДС индукции на концах проводника в
конце движения равна 2 В?
оризонтально
расположенный проводник длиной 1 м
движется равноускоренно в вертикальном
однородном магнитном поле, индукция
которого направлена перпендикулярно
проводнику и скорости его движения (см.
рисунок). При начальной скорости
проводника, равной нулю, и ускорении
8 м/с2, он переместился
на 1 м. Какова индукция магнитного
поля, в котором двигался проводник, если
ЭДС индукции на концах проводника в
конце движения равна 2 В?
Один
из вариантов решения задачи. ЭДС
индукции в проводнике, движущемся в
однородном магнитном поле, может быть
рассчитана с помощью формулы закона
определяется выражением
![]() ,
где, в свою очередь dS –
площадь – определяется произведением
Фарадея:
,
где, в свою очередь dS –
площадь – определяется произведением
Фарадея:
![]() ,
где изменение магнитного потока за
малое время dt длины
проводника ℓ на его малое перемещение
dх за интервал времени
dt; т.е.
,
где изменение магнитного потока за
малое время dt длины
проводника ℓ на его малое перемещение
dх за интервал времени
dt; т.е.
![]() .
.
Таким образом,
![]() =
Blv,
где v–скорость движения
проводника в некоторый
=
Blv,
где v–скорость движения
проводника в некоторый
момент времени t.
Отсюда B =
![]() .
.
Определим скорость v в
конце пути длиной X.
Согласно уравнениям кинематики:
 .
Отсюда
.
Отсюда
![]() ;
;
![]() .
.
Задача 13. Металлическое кольцо, диаметр которого 20 см, а диаметр провода кольца 2 мм, расположено в магнитном поле, магнитная индукция которого меняется по модулю со скоростью 1,09 Тл/с. Плоскость кольца перпендикулярна вектору магнитной индукции. Возникающий в кольце индукционный ток 10 А. Определите удельное сопротивление металла, из которого изготовлено кольцо.
О дин
из вариантов решения задачи. ЭДС
индукции в кольце ε = -
дин
из вариантов решения задачи. ЭДС
индукции в кольце ε = -![]() .
Изменение магнитного потока за время
Δt равно ΔФ
= Δ(BS), где
S (площадь кольца) постоянна
и равна S =
.
Изменение магнитного потока за время
Δt равно ΔФ
= Δ(BS), где
S (площадь кольца) постоянна
и равна S =![]() .
Следовательно, |ε| = S
.
Следовательно, |ε| = S![]() .
По закону Ома для участка цепи ε
= IR = I
.
По закону Ома для участка цепи ε
= IR = I![]() ,
где Snp
- площадь сечения медного провода кольца
Snp
=
,
где Snp
- площадь сечения медного провода кольца
Snp
=![]() ,
длина кольца l =
πD.
,
длина кольца l =
πD.
Приравнивая выражения для ЭДС, получим
плотность вещества, из которого
изготовлено кольцо: ρ =![]() .
Медь: ρ ≈1,7·10-8 Oм·м.
.
Медь: ρ ≈1,7·10-8 Oм·м.
З адача
14. Кольцо
из тонкой проволоки сопротивлением R
ограничивает на плоскости круг площадью
S
= 0,1 м2,
в пределах которого внешнее магнитное
поле однородно. Вектор магнитной индукции
В перпендикулярен плоскости круга (см.
рисунок, вид сверху). За пределами круга
магнитное поле пренебрежимо мало. Какое
напряжение покажет вольтметр с внутренним
сопротивлением r,
подключенный к точкам 1 и 2, которые делят
длину кольца в отношении 1:2? Магнитное
поле меняется с течением времени t
так, что
адача
14. Кольцо
из тонкой проволоки сопротивлением R
ограничивает на плоскости круг площадью
S
= 0,1 м2,
в пределах которого внешнее магнитное
поле однородно. Вектор магнитной индукции
В перпендикулярен плоскости круга (см.
рисунок, вид сверху). За пределами круга
магнитное поле пренебрежимо мало. Какое
напряжение покажет вольтметр с внутренним
сопротивлением r,
подключенный к точкам 1 и 2, которые делят
длину кольца в отношении 1:2? Магнитное
поле меняется с течением времени t
так, что
![]() = 0,01 Тл/с, а
= 0,01 Тл/с, а
![]() =
10.
=
10.
Один из вариантов решения задачи. Выберем направления и обозначения для токов i1 i2, i3 в соответствии с условием задачи. Запишем систему уравнений:
закон Ома для простого
замкнутого контура, i1![]() + i2
+ i2![]() =ξ;
=ξ;
закон Ома для простого замкнутого контура, образованного нижней частью кольца и участком цепи, содержащим вольтметр, i2 - i3r = 0;
условие стационарности токов, i1=i2+ i3 ;
закон электромагнитной индукции, ξ=S ;
закон Ома для участка цепи Uv= i3r.
Выполнив математические
преобразования, получаем ответ в общем
виде: Uv
= и числовой ответ: Uv
= 326 мкВ.
и числовой ответ: Uv
= 326 мкВ.
Задача 15. Плоская горизонтальная фигура площадью S = 0,1 м2, ограниченная проводящим контуром, с сопротивлением R = 5 Ом, находится в однородном магнитном поле. Пока проекция магнитной индукции на вертикаль z медленно и равномерно убывает от некоторого начального значения Bjz до конечного значения B2z = - 1 Тл, по контуру протекает заряд Δq = 0,08 Кл. Найдите B1z.
Один
из вариантов решения задачи. В случае
однородного поля по закону электромагнитной
индукции
![]() .
С другой стороны, |εi
| = IR. Поэтому |Δq|
= IΔt = =
.
С другой стороны, |εi
| = IR. Поэтому |Δq|
= IΔt = =![]() |В2z
– B1z|.
Отсюда В1z
= В2z
+
|В2z
– B1z|.
Отсюда В1z
= В2z
+![]() =
-1+
=
-1+![]() =
3 (Тл).
=
3 (Тл).
Задача 16. Плоская катушка диаметром 6 см, состоящая из 120 витков, находится в однородном магнитном поле, индукция которого 6·10-2 Тл. Катушка поворачивается вокруг оси, перпендикулярной линиям индукции, на угол 180° за 0,2 с. Плоскость катушки до и после поворота перпендикулярна линиям индукции поля. Чему равно среднее значение ЭДС индукции, возникающей в катушке?
Один
из вариантов решения задачи. ЭДС
индукции в катушке: ε =
-n
.
Изменение магнитного потока за время
Δt равно ΔФ
= Ф2 Ф1= BS(cos
α2 – cos
α1), где S=
,
cosα2 =-1, cos
α1 = +1. Следовательно,
ΔФ = -![]() .
ε =- n
.
ε =- n![]() .
ε ≈ 0,2 В.
.
ε ≈ 0,2 В.
З адача
17. Квадратную рамку из
медной проволоки со стороной b
= 5 см и сопротивлением R
= 0,1 перемещают вдоль оси Ох по гладкой
горизонтальной поверхности с
постоянной скоростью V
= 1 м/с. Начальное положение рамки
изображено на рисунке. За время движения
рамка успевает пройти между полюсами
магнита и оказаться в области, где
магнитное поле отсутствует. Ширина
полюсов магнита d
= 20 см, магнитное поле имеет резкую
границу и однородно между полюсами.
Возникающие в рамке индукционные токи
нагревают проволоку, в которой за все
время движения выделяется количество
теплоты Q
= 2,5·10-3
Дж. Чему равна индукция магнитного поля
В между полюсами?
адача
17. Квадратную рамку из
медной проволоки со стороной b
= 5 см и сопротивлением R
= 0,1 перемещают вдоль оси Ох по гладкой
горизонтальной поверхности с
постоянной скоростью V
= 1 м/с. Начальное положение рамки
изображено на рисунке. За время движения
рамка успевает пройти между полюсами
магнита и оказаться в области, где
магнитное поле отсутствует. Ширина
полюсов магнита d
= 20 см, магнитное поле имеет резкую
границу и однородно между полюсами.
Возникающие в рамке индукционные токи
нагревают проволоку, в которой за все
время движения выделяется количество
теплоты Q
= 2,5·10-3
Дж. Чему равна индукция магнитного поля
В между полюсами?
Один
из вариантов решения задачи. При
пересечении рамкой границы области
поля со скоростью V
изменяющийся магнитный поток создает
ЭДС индукции εинд =-
= VBb. Сила тока в это время
равна I=![]() .
При этом в проволоке выделяется
количество теплоты Q =
I2Rt,
где t - время протекания
тока. Ток течет в рамке только во время
изменения магнитного потока – при входе
в пространство между полюсами и при
выходе. Это время
.
При этом в проволоке выделяется
количество теплоты Q =
I2Rt,
где t - время протекания
тока. Ток течет в рамке только во время
изменения магнитного потока – при входе
в пространство между полюсами и при
выходе. Это время
t
= 2![]() .
Подставляя значения тока и времени,
получим В =
.
Подставляя значения тока и времени,
получим В =
![]() =
1 Тл.
=
1 Тл.
Один из
вариантов решения задачи. При
максимальном заряде на конденсаторе
сила тока в цепи равна нулю. Изменение
заряда конденсатора Q
= Qmax - CU0
(1). Изменение энергии конденсатора
W=
![]() (2). Работа, совершенная батареей, А =
Q·
= ·(Qmax - CU0)
(3). По закону сохранения энергии
(омическим сопротивлением пренебрегаем,
а энергия катушки равна нулю) совершенная
работа равна изменению энергии
конденсатора. Приравнивая (2) и (3), и
учитывая U0 = 0,5,
получаем квадратное уравнение для
Qmax:
Qmax2 – 2C
Qmax
+
(2). Работа, совершенная батареей, А =
Q·
= ·(Qmax - CU0)
(3). По закону сохранения энергии
(омическим сопротивлением пренебрегаем,
а энергия катушки равна нулю) совершенная
работа равна изменению энергии
конденсатора. Приравнивая (2) и (3), и
учитывая U0 = 0,5,
получаем квадратное уравнение для
Qmax:
Qmax2 – 2C
Qmax
+
![]() C22 = 0.
У квадратного уравнения есть два решения
Q´max
=
C22 = 0.
У квадратного уравнения есть два решения
Q´max
=
![]() C
и Q´´max=
C
и Q´´max= ![]() C.
Второе решение соответствует начальному
состоянию. Поэтому решением задачи
является первое значение
C.
Второе решение соответствует начальному
состоянию. Поэтому решением задачи
является первое значение
Qmax= C = 30 мкКл.
