Ответы ТОЭ

1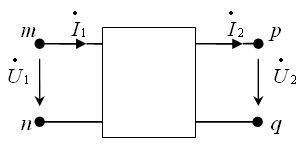) Какие электрические цепи можно представить пассивным или активным четырехполюсником? Приведите несколько примеров. В виде пассивного или активного четырехполюсника можно представить такие электрические цепи (части электрических цепей), имеющие две пары зажимов, одна из которых является входной, а другая выходной. Его принято изображать в виде прямоугольника с выходящими из него концами (полюсами) mn и pq. Пассивным четырехполюсником называется четырехполюсник, не имеющий в своих ветвях источников электрической энергии. Активным четырехполюсником называется четырехполюсник, имеющий в своих ветвях источники электрической энергии. Примеры: линии электропередач, трансформаторы, мостовая схема, усилители и т.д.

2) Уравнения четырехполюсников. Приведите пример записи уравнений в какой либо форме. Помимо того, что четырехполюсники делятся на активные и пассивные, их можно разделить по формам записи уравнений четырехполюсника. А-форма: соответствует положительным направлениям токов и напряжений.

3) Сколько и каких опытов необходимо провести для определения параметров (постоянных) четырехполюсников? Так как у четырехполюсника 4 параметра (A, B, C, D), то для их определения необходимо составить систему из 4 уравнений: 1) основано на принципе взаимности . 2) Опыт ХХ при разомкнутых выходных зажимах: 3) Опыт К.З.: 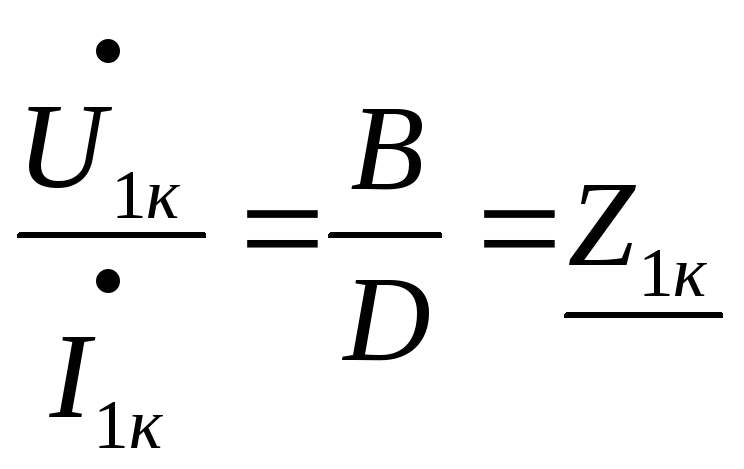4) Опыт ХХ при разомкнутых входных зажимах:

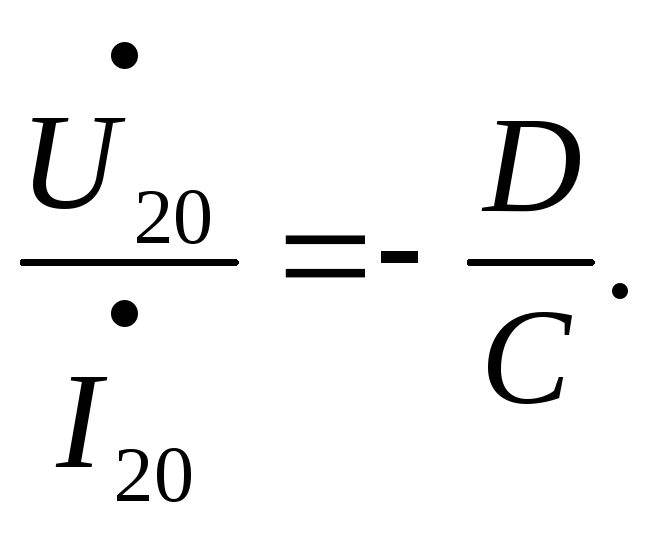
4) Симметричный четырехполюсник. Как опытным путем обнаружить, что данный четырехполюсник – симметричный? Четырехполюсник называют симметричным, если при перемене местами источника питания и нагрузки, токи в источнике питания и нагрузке не изменяются. В симметричном четырехполюснике . А-форму записи можно представить в виде: , где . Симметрию можно обнаружить путем перемены клемм mn и pq местами, то есть mn к нагрузке, pq к источнику. При питании со стороны источника измеряют нагрузки, после перемены местами нагрузки и источника при должно быть .

5) Перечислить различные способы соединения несимметричных четырехполюсников. Способы соединения четырехполюсников «а» и «б»: а)последовательное (Z-форма) б)параллельное (Y-форма) в) последовательно-параллельное (Н-форма) г)параллельно-последовательное (G-форма) д)каскадное (А-форма).

Z-форма:

6) Поясните смысл понятии – повторное сопротивление четырехполюсника. Повторное сопротивление четырехполюсника – это такое входное сопротивление, которое равно (повторяет) сопротивлению нагрузки. . Если четырехполюсник симметричный, то .

7) Смысл понятия коэффициента передачи (распространения) симметричного четырехполюсника. Коэффициент передачи является параметром, характеризующим четырехполюсник с точки зрения передачи полной мощности через него. Коэффициент передачи определяется как . Вещественная часть , то есть называется коэффициентом затухания, а мнимая, то есть - Коэффициент фазы четырехполюсника.

8) Согласованный режим четырехполюсника. Условие при котором возможен такой режим. Согласованным режимом работы четырехполюсника называется режим при котором . При этом в месте включения четырехполюсника не будут возникать отраженные волны, или, говоря иначе в цепи не будет возникать добавочного затухания и вся мощность передастся в нагрузку. С этой целью к согласованному режиму стремятся в цепях слабого тока (радио, телефон, телеграф и т.д.) с целью более правильной работы аппаратуры.

9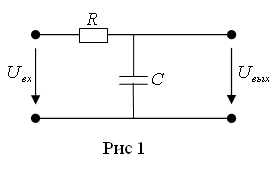) Применение простейших в качестве интегрирующих и дифференцирующих цепей. Условия, при которых данные цепи выполняют такие функции. Четырехполюсник применяют в качестве интегрирующей цепи (рис. 1), если выполняется условие: , то есть если . Тогда . четырехполюсник применяют в качестве дифференцирующей цепи (рис. 2), если выполняется условие: , то есть если . Тогда

10) Применение понятий – передаточная функция по току и напряжению для расчета переходных режимов четырехполюсников. Передаточная функция по току и напряжению – применяется для расчета переходных режимов четырехполюсников. Передаточная функция по напряжению: . Передаточная функция по току: .

11) Приведите примеры электрических цепей с распределенными параметрами. 1.Электрическая цепь с распределенными параметрами – это цепь, в которой сопротивления, проводимости, индуктивности и емкости распределены вдоль линии. 2. Электрической цепью с распределенными параметрами называется такая цепь, в которой для одного и того же момента времени ток и напряжение изменяются непрерывно при переходе от одной точки цепи к соседней. Примеры: обмотка электрической машины, трансформатора, антенна радиотехнического устройства, длинная электрическая линия.

12) Приведите схему замещения участка цепи с распределенными параметрами – двухпроводной линии. На рисунке изображена схема электрической цепи, состоящая из источника и приемника электрической энергии, связанных двухпроводной линией (рис 1).Представим схему замещения такой электрической цепи (рис. 2).

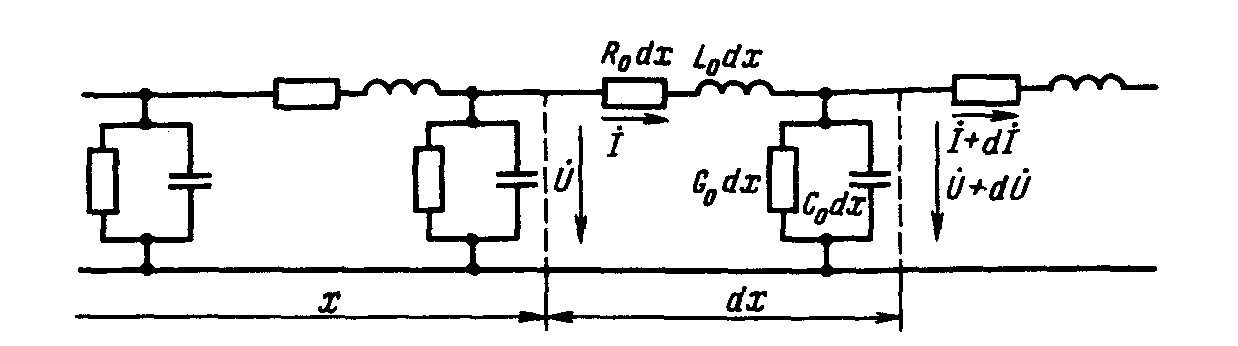
Рис1 Рис2

На схеме замещения бесконечно малый участок двухпроводной линии длиной представлен ячейкой с активным сопротивлением прямого и обратного проводов, индуктивностью , проводимостью и емко­стью между проводами.

13) Какие физические явления учитывают параметры в линии с распределенными параметрами? Параметры учитывают то, что сопротивления, проводимости, индуктивности и емкости равномерно распределены вдоль линии, а также учитывают соответственно следующие физические явления: преобразование электрической энергии в тепловую () и обратное ей (), электрической энергии в энергию магнитного поля (), и явление накопления электрической энергии ().

14) Смысл понятий – прямая (падающая), обратная (отраженная) волны в линии с распределенными параметрами. Прямая (падающая) волна – 1)волна, распространяющаяся от источника энергии к приемнику (в сторону увеличения координаты х), которая несет энергию, заключенную в ее электрическом и магнитном полях 2) процесс перемещения электромагнитного состояния от источника энергии к приемнику.. Обратная (отраженная) волна – 1) процесс перемещения электромагнитного состояния от приемника энергии к ее источнику 2) волна, распространяющаяся от приемника энергии к источнику (в сторону уменьшения координаты х), которая несет энергию, заключенную в ее электрическом и магнитном полях.

15) Длина волны и Фазовая скорость в линии, смысл этих понятий. Длина волны - 1)расстояние, взятое в направлении распространения волны, между ближайшими двумя точками, фазы колебания в которых различаются на .2)расстояние, которое пробегает волна за время, равное периоду. Фазовая скорость - 1)скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания. 2) скорость перемещения фазы колебания, которая в течении времени и по мере увеличения расстояния, пройденного волной остается постоянной.3)фазовая скорость – это скорость перемещения по линии неизменного фазового состояния. .

16) Понятие - коэффициент отражения в конце и начале линии. Вычисление этих величин через . Коэффициент отражения (по напряжению) - отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии. . При согласованной нагрузке , при холостом ходе . Коэффициент отражения по току . В начале линии .

17) Коэффициент распространения и повторное сопротивление в линии, смысл и определение этих параметров. Повторное сопротивление в линии это такое входное сопротивление, которое повторяет сопротивление нагрузки. . Коэффициент передачи является параметром, характеризующим четырехполюсник с точки зрения передачи полной мощности через него. Коэффициент передачи определяется как . Вещественная часть , то есть называется коэффициентом затухания, а мнимая, то есть - Коэффициент фазы четырехполюсника.

18) При каких условиях линия является линией без искажений. Как на практике достигается в реальных линиях выполнение этих условий? Линия без искажения – линия, вдоль которой волны всех частот распространяются с одинаковой скоростью и затухают в равной степени. Для того, чтобы линия являлась линией без искажения необходимо, чтобы коэффициент затухания и фазовая скорость не зависели от частоты; и не зависят от частоты, если между параметрами линии выполняется следующее соотношение: . На практике это достигается путем включения в линию дополнительных индуктивностей.

19) Различные режимы работы линии без потерь. Стоячие волны. Линия без потерь не существует в природе, но можно добиться условий при которых потерь будут минимальны. Линия без потерь будет тогда, когда и будут равны нулю (или очень малыми по сравнению с и соответственно) .Режимы работы линии без потерь: холостой ход, короткое замыкание, режим с согласованной нагрузкой, режим с несогласованной нагрузкой. Стоячая электромагнитная волна – это электромагнитная волна, полученная в результате наложения движущихся навстречу падающей и отраженной волн одинаковой интенсивности.

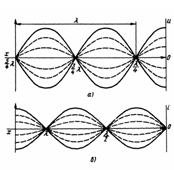
20) Входное сопротивление отрезка линии без потерь. Возможность представления этих отрезков в виде идеальных реактивных элементов .Входное сопротивление – 1)сосредоточенное сопротивление, которым можно заменить линию вместе с приемником на ее конце при расчете режима в начале линии. 2)отношение комплекса напряжения к комплексу тока в начале линии, при нагрузке которое также можно выразить через входное сопротивление при холостом ходе и коротком замыкании : .

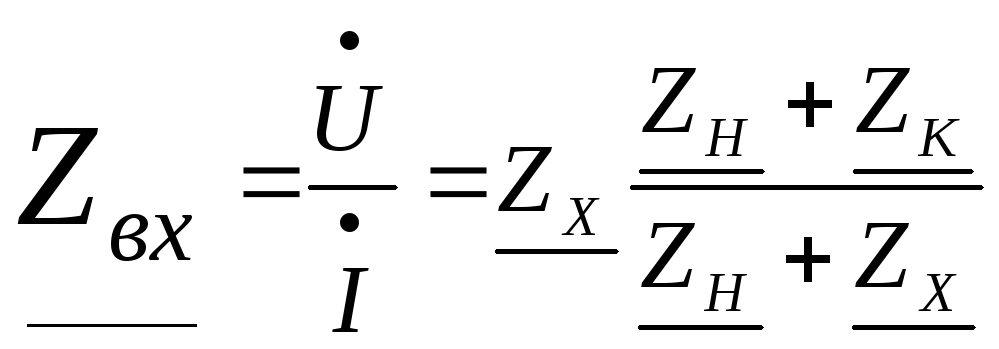21) Какой из перечисленных режимов длинной линии является согласованным? Согласованный режим нагрузки – это такой режим, при котором сопротивление нагрузки в конце линии равно ее волновому сопротивлению. То есть: . При согласованном режиме отраженных волн в линии нет, следовательно, энергия, которую несет падающая волна, полностью поглощается в нагрузке.

22) Почему наиболее опасным является режим включения длинной линии разомкнутой на конце на постоянное напряжение? Этот режим является наиболее опасным так как на постоянном напряжении на ХХ коэффициент отражения , в результате чего прямая и отраженная волны складываются и напряжение в конце линии становится в 2 раза больше.

23) Дайте определение функций, описывающих распределение и движение зарядов – объемная плотность заряда и вектор плотности . Плотность электрического заряда – величина, характеризующая распределение электрических зарядов в пространстве. В зависимости от того, как распределены заряды, различают: линейную плотность заряда, поверхностную, и объемную. Объемная плотность заряда: , где - электрический заряд, находящийся в малом элементе объема . Единица размерности – . - вектор плотности тока проводимости – учитывает движение заряда в проводящей среде. .

24) Исходя из формулы Лоренца дайте определение векторов напряженности и магнитной индукции . Формула Лоренца . Если заряд неподвижен то ввиду отсутствия второго слагаемого в формуле напряженность электрического поля можно определить как отношение величины силы Лоренца к величине заряда, на который она действует: . Если заряд находится в движении, то можно определить вектор магнитной индукции. . . То есть если взять заряд то при скорости и силе значение магнитной индукции будет равно 1 Тесло. Магнитная индукция – это сила с которой действует магнитное поле на движущуюся частицу.

25) Дайте определение векторов электрического смещения и напряженности магнитного поля . Вектор электрического смещения – вектор, введенный для описания электрического поля поляризованного диэлектрика (без учета связанных зарядов).,где -поляризованность диэлектрика

-вспомогательная функция для расчета магнитных полей без учета микротоков (А/м)

26) Связь между основными и вспомогательными векторами, описывающими электромагнитное поле. Диэлектрическая и магнитная проницаемость вещества и . и , где и - это параметры, характеризующие среду.

27) Связь между векторами и в проводящей среде. Закон Ома в дифференциальной форме. - удельная проводимость. - закон Ома в дифференциальной форме - связь между векторами в проводящей среде, - удельная электрическая проводимость

28) Формулы для вычисления энергии электрического и магнитного полей. , ,

29) Скалярная функция, описывающая электрическое поле – потенциал. Определение величины и физический смысл. Скалярная величина , являющаяся энергетической характеристикой электрического поля, равная работе по переносу заряженной частицы из одной точки в точку нулевого потенциала : 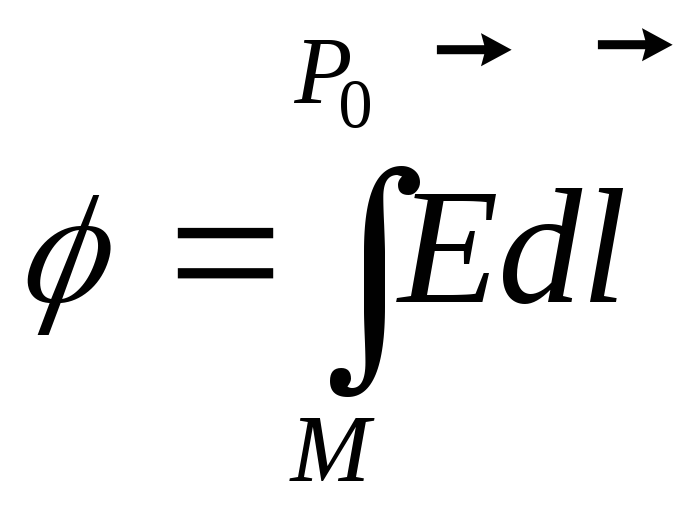. Потенциал связан с напряженностью электрического поля . Единица измерении – вольт.

30) Сторонние силы в электрическом поле . Их природа, примеры. Сторонние силы – силы, действующие на заряженные частицы и тела, но не являющиеся ни силами электростатического поля, ни силами индуцированного электрического поля, то есть обусловленные химическими реакциями, контактными явлениями, тепловыми, механическими и другими процессами, происходящими в источниках питания электрических цепей. Пример: щелочная, солевая батарейка и т.п.

31) Описание сторонних сил в электрическом поле с помощью вектора . Определение этой величины. Сторонние силы - силы, имеющие не электрическую природу(фотоэффект, химических реакций)

32) Виды эл. тока и описание этого явления с помощью векторов плотности тока проводимости, переноса, и эл. смещения. Ток - физическая величина, равная потоку вектора плотности тока через некоторую поверхность. Различают ток проводимости , где , ток смещения , где и ток переноса , где (для большинства задач отсутствует).

33) Интегральные характеристики поля: напряжение и магнитное напряжение . Определение этих величин. ,, напряжение - физическая величина численно равная работе по перемещению единичного заряда вдоль пути ab.

34) Интегральные характеристики поля: электрический ток i и магнитный поток Ф. Определение этих величин. , . Электрический ток – всякое упорядоченное движение электрических зарядов, магнитный поток Ф через некоторую поверхность S - это поток вектора магнитной индукции через эту поверхность (единица Вебер).

35) Интегральная характеристика ЭДС, определение и физический смысл. ЭДС – энергетическая характеристика неэлектростатического электрического поля. ЭДС равна отношению работы, совершаемой сторонними силами к перенесенному электрическому заряду между двумя точками вдоль рассматриваемого пути или вдоль замкнутого контура.(1 Дж/1 Кл)=(1 В).

36) Закон Ома на постоянном токе, тепловая мощность и энергия - закон Джоуля-Ленца. -закон Ома для участка цепи,-закон Ома для всей цепи,-закон Джоуля-Ленца.

37) Электрическая ёмкость - С. Три определения ёмкости: через заряд, тока смещения и энергию электрического поля. С - коэффициент пропорциональности, определяющий заряд, который надо сообщить телу, чтобы вызвать повышение его потенциала на 1 В. Единица измерения – Фарадей(1 Кл/1 В)=(1 Ф) , ,

38) Понятие эл. сопротивления. Какие явления учитывает этот параметр? При наличии электрического тока в проводниках движущиеся свободные электроны, сталкиваясь с ионами кристаллической решетки, испытывают противодействие своему движению. Это противодействие количественно оценивается сопротивлением цепи. За единицу сопротивления принято сопротивление такого участка цепи, в котором устанавливается ток в 1 Ампер при напряжении 1 Вольт.

,этот параметр учитывает выделение теплоты на участке цепи (превращение электрической энергии в тепловую)

39) Схема замещения реального конденсатора, смысл её параметров. Идеальный конденсатор. В реальном конденсаторе существуют активные потери (ток утечки), поэтому на схеме он изображается с подключенным параллельно ему сопротивлением. На рисунке ток I₁ – ток смещения, а I₂-ток утечки, тангенс δ - тангенс угла диэлектрических потерь, в идеальном же конденсаторе нет потерь, вся энергия накапливается в электрическом поле (тангенс δ равен 0)