8. Проверка гипотезы о гетероскедастичности остатков.

H₀ – нулевая гипотеза о том, что остатки гетероскедастичны, H₁ - что гетероскедастичность отсутствует. На следующей страницы графический анализ.

Гистограмма остатков, полученных из функции “regression”.

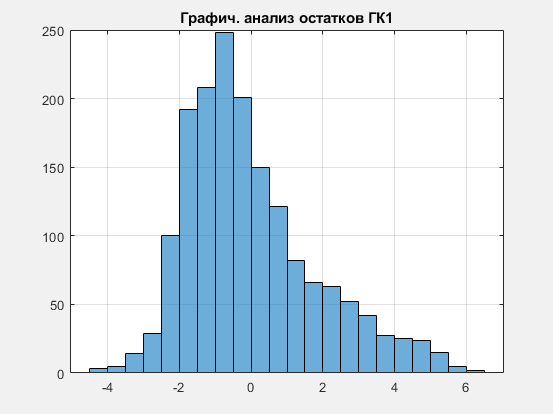
Рисунок 7 Графический анализ остатков 1 ГК.

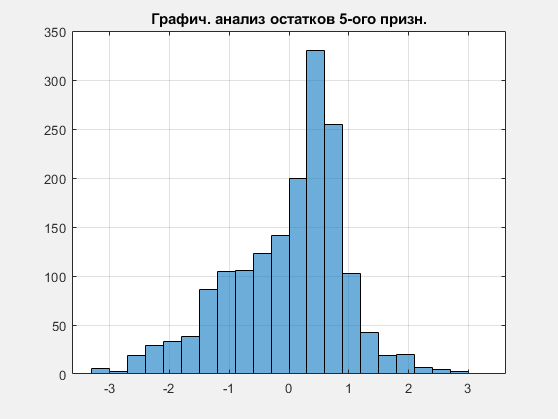
Рисунок 8 Графический анализ остатков 5-ого призн.

Как видно из графика, остатки (по сути разброс второй ГК относительно первой) убывают. Из чего можно сделать вывод, что остатки гетероскедастичны.

Проверим эту же гипотезу с помощью теста ранговой корреляции Спирмана:

При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значений X. Поэтому для регрессии, построенной по МГК, абсолютные величины отклонений ε_i и значения х_i будут коррелированны.

Значения х_i и ε_i ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

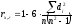
где d_i — разность между рангами х_i и ε_i, i = 1, 2, ..., n;

n — число наблюдений.

n=length(PC1); % Тест Спирмана

XR1=[PC1 r];

XR=sortrows(XR1);

[~,IR]=sort(XR(:,1),1);

[~,IX]=sort(XR(:,2),1);

Rangs=1-(6*sum((IX-IR).^2)/(n^3-n));

t1=Rangs*((n-2)^(1/2))/((1-Rangs^2)^(1/2)); %Коэф. Стьюдента

[RHO,~] = corr(PC1,r,'type','Spearman');

t=1.96;

Otnoshenie=abs(t1/t); %если больше 1, то гетероскедастичны , если меньше 1 , то гомоскедастичны

n в этом случае берем как «длину» одной из главных компонент.

t1 получаем равным -0.7535, что меньше 1.96. Из чего так же делаем вывод что остатки гетероскедастичны.

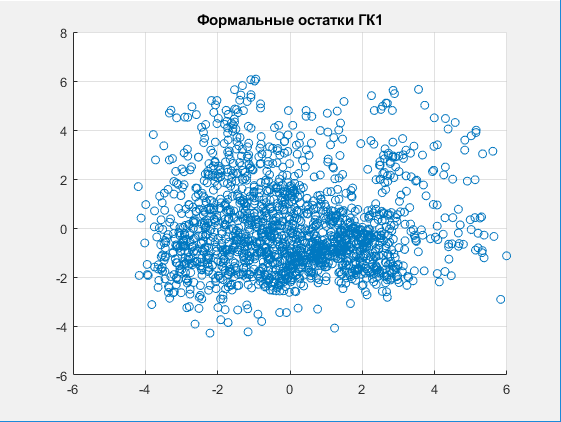
Рисунок 9 Скаттерограмма в пространстве формальных остатков 1 ГК.

Рисунок 10 Скаттерограмма в пространстве формальных остатков 5-ого призн.

9. Вывод

В результате обработки статистических данных изучен один из основных способов уменьшения размерности данных – Метод Главных Компонент (далее МГК). На основе выборки из 2000 строк данных, отличающихся по 16 атрибутам и разделенных на 2 класса, путем применения МГК рассчитывается вклад каждого атрибута.

Среда Matlab предлагает встроенные функция применения этого метода, возвращающая матрицу главных компонент, матрицу множества данных ГК, дисперсии ГК. Однако перед применением этого метода необходимо:

1. Удалить выбросы

2. Пронормировать исходные данные, так как заранее неизвестна схема вклада каждого атрибута на флаг.

3. Уровнять представителей классов.

Удаляем выбросы по правилу трех сигм. Каждую строку, в которой атрибут превосходит математическое ожидание и 3 СКО удаляем, пологая, что это ошибочные данные.

Перед нормированием и удалением выбросов вклад первой ГК был около 90%, после – в районе 20%. В результате на итоговых графиках мы не видим четкого разделения классов по двум ГК. Немного лучше ситуация обстоит в пространстве 3 ГК. Несмотря на значительные уменьшения вклада первого атрибута, мы не имеем право использовать ненормированную матрицу.

Так же для улучшения результатов применения МГК прировняем количество представителей классов (меток «0» и «1»), удалив лишние данные. В результате обработки получаем матрицу с 1674 строками, которую делят поровну оба класса.

Теперь данные готовы к применению МГК. В результате работы функции PCA(X), получаем векторы-столбцы данных – главные компоненты. Судить о их вкладе можно путем анализа «нагрузки» (latent) (буквально это дисперсия – разброс данных относительно ГК). Пункт 6 позволяет наглядно представить разделение классов по соответствующим ГК. Классы наиболее хорошо разделены в том случае, если их гистограммы так же хорошо разделены. Выбираем ГК с наибольшим вкладом, в их пространстве строим скаттерограмму.

Как видно в соответствующих пунктам, в результате этой обработки мы можем видеть довольно хорошо разделенные классы.

Для построения линейной регрессии так же используем стандартную функцию среды расчетов Matlab – regression, которой передадим как аргументы значения двух ГК. В результате обработки, функция вернет нам: b – кофф. наклона касательной, r – остатки значений относительно нее. Код представлен в соответствующем пункте. Так как значения нормированы (сдвинуты на их мат. ожидание) и первая ГК стремится охватить наибольшую дисперсию, получаем линию, параллельную оси первой ГК. На графике в пункте это хорошо видно.

Гетероскедастичность остатков в целом говорит о том, что дисперсия (разброс второй ГК) не растет относительно первой (при увеличении/уменьшении). Гистограмма это хорошо отображает, однако на графике остатков при этих значениях однозначно сложно об этом говорить.

Для более качественной (эмпирической) проверки гипотезы о гетероскедастичности остатков применим тест ранговой корреляции Спирмена. Значения первой ГК и остатков (по сути значения второй ГК в нашем случае, но в более общем однозначно остатков) ранжируются (упорядочиваются по величинам – сортируются). В результате получаем ранги, из которых, по формуле, получаем коэффициент корреляции t1 = -0.7535 , что не превосходит коэффициент Стьюдента. Откуда можно сделать вывод, что остатки гетероскедастичны.

При анализе корреляции для 5 и 10 классов, я получил коэффициент -0.7535, что говорит об отсутствии гетероскедастичности. Таким образом, можно говорить, что остатки для первых двух ГК имеют нормальное распределение, но, допустим, для взятого для примера 5 и 10 признака, они не распределены по нормальному закону.