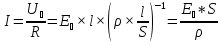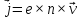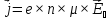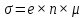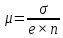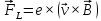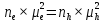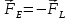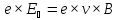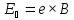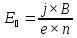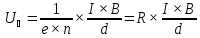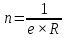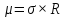Национальный исследовательский университет "МЭИ"

Кафедра Физики и Технологии Электротехнических

Материалов и Компонентов (ФТЭМК)

Лабораторная работа

“Эффект Холла в примесном полупроводнике”

Выполнили

Проверил преподаватель:

Профессор кафедры ФТЭМК,

д-р физ.-мат. наук,

академик Российской Академии

Инженерных Наук им. А.М. Прохорова

2016 г

Эффект Холла в примесном полупроводнике

Цель работы: определение концентрации и подвижности основных носителей заряда.

Теоретические сведения

Эффект Холла занимает важнейшее место в группе так называемых гальваномагнитных эффектов — эффектов, связанных с воздействием магнитного поля на электрические свойства проводников (металлов и полупроводников) по которым течёт ток. Величина эффекта Холла непосредственно связана с подвижностью и концентрацией носителей заряда, а знак (направление) ЭДС Холла (ХЭДС) зависит от знака заряда. По данной причине эффект Холла находит широкое применение при исследовании электрических свойств.

Подвижными носителями заряда в полупроводниках являются как электроны, так и дырки. Дырка – это фактически частично заполненная валентная связь, которая проявляет себя как подвижный положительный заряд, численно равный заряду электрона. Для определенности рассмотрим поведение в эффекте Холла подвижных положительных зарядов. Этот подход будет применим для тех полупроводников, в которых преобладает концентрация примесей акцепторного типа. Например, для кремния и германия такими примесями являются бор, алюминий, галлий, индий. Для полупроводниковых материалов с преобладанием донорных примесей (фосфор, мышьяк, сурьма) качественно рассмотрение будет полностью аналогичным, за исключением противоположного знака основных носителей заряда.

При приложении к проводящему материалу внешнего электрического поля 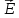(в дальнейшем мы будем называть его продольным и обозначать 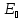), возникает направленное движение заряженных частиц — электрический ток, сила которого определяется законом Ома:

1

где - электрическое напряжение, - значение удельного сопротивления материала образца, 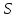- площадь поперечного сечения, - длина образца.

При преобладании дырочного типа проводимости положительные носители заряда движутся со средней дрейфовой скоростью 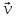в направлении вектора плотности тока :

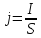2

где 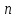— концентрация носителей, 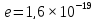Кл – элементарный заряд.

Величина скорости направленного дрейфа носителей заряда и напряженность продольного электрического поля 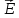при не слишком больших значениях напряженности (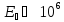 В/м) могут быть связаны простым соотношением пропорциональности:

3

где 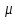— коэффициент, называемый подвижностью носителя заряда.

Величина подвижности зависит от температуры и от типа носителя заряда. Подвижности электронов и дырок в различных полупроводниках могут отличаться более чем на порядок.

Из соотношений и следует:

4

Удельная проводимость материала образца (величина, обратная к удельному сопротивлению) 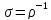будет равна:

5

При известной концентрации носителей 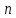, можно определить их подвижность:

6

Поместим теперь наш образец с электрическим током в однородное постоянное магнитное поле, вектор индукции 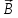которого направлен перпендикулярно вектору плотности тока 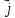. В данном магнитном поле на заряды, движущиеся со скоростью 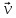, действует сила Лоренца:

7

Эта сила ориентирована перпендикулярно к векторам 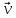и 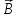. Под ее действием поток зарядов отклоняется в сторону от первоначального направления вектора 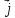(рис. 1). В результате на одной грани образца накапливается некоторый положительный электрический заряд, а на противоположной грани возникает такой же по модулю избыточный отрицательный заряд. Данная поляризация образца приводит к возникновению поперечного электрического поля 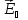, направленного перпендикулярно и току и магнитному полю.

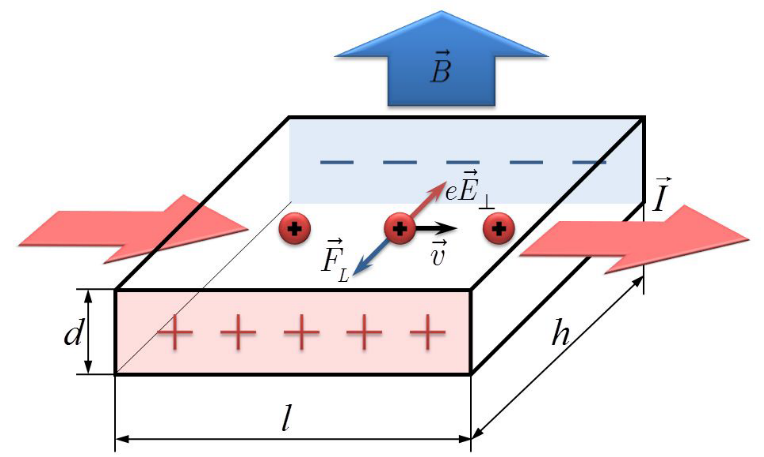
рис. 1 Принцип возникновения ХЭДС

Если же свободными носителями заряда являются преимущественно электроны, то ближняя к нам по рис. 1 грань образца заряжается отрицательно, а дальняя – положительно, так как направление силы Лоренца, поляризующей образец, останется прежним — в формуле изменится знак, как у заряда носителя, так и у вектора дрейфовой скорости. Таким образом, направление поля Холла 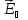при заданных направлениях магнитного поля и тока зависит от знака основных носителей заряда.

Отметим, что при наличии в полупроводнике носителей зарядов разных знаков в сопоставимом количестве, эффект Холла будет отсутствовать при выполнении следующего условия:

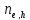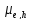где и - концентрации и подвижности электронов и дырок.

Процесс разделения электрических зарядов противоположных знаков продолжается до тех пор, пока напряженность поля 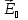не возрастет до значения, при котором электрическая сила 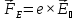станет равна силе Лоренца:

8

после чего наступает равновесное состояние. Если наряду с условием равновесия учесть соотношение, то для холловского поля можно записать выражение:

9

Разность потенциалов между ближней и дальней гранями образца равна напряженности электрического поля 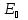, умноженной на размер образца 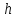. Таким образом, значение измеряемого поперечного (холловского) напряжения можно представить как 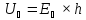. Площадь поперечного сечения равна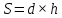, где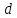 - толщина образца в направлении линий индукции магнитного поля, а плотность тока 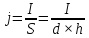, следовательно, выражение может быть записано в виде

10

где коэффициент 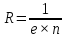носит название константы Холла.

Определив 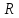, можно непосредственно рассчитать величину концентрации носителей заряда n в материале образца:

11

С учетом подвижность носителей определяется как произведение проводимости материала на значение константы Холла:

12

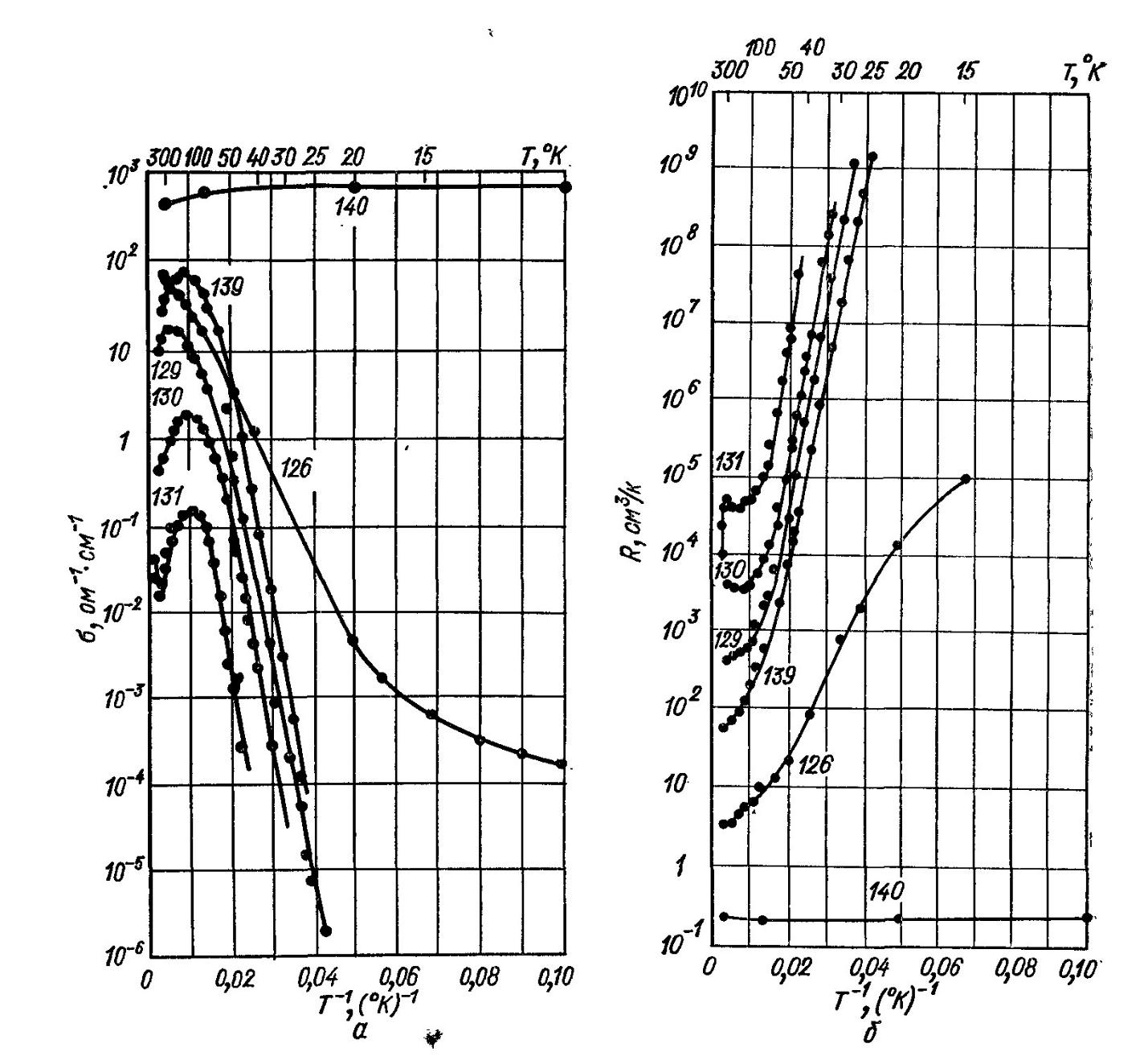
рис. 2 Зависимость удельной проводимости σ n-Si с примесью As (а) и постоянной Холла R в n-Si (б) от температуры.

Результаты измерений

Образец №126

Таблица 1 Результаты измерений

T, K	1/T, 1/K	σ, 1/(Ом*см)	R, (см^(3))/(K)	n, см^(-3)	μ, (см^(2))/(В·с)	ln(σ)
300	0,003	85	5	1,25E+18	425	4,44
140	0,007	70	6	1,042E+18	420	4,25
100	0,01	55	8	7,812E+17	440	4,01
83	0,012	22	10	6,25E+17	220	3,09
50	0,02	6	40	1,563E+17	240	1,79
40	0,025	2	90	6,944E+16	180	0,69
20	0,05	0,007	9E+2	6,944E+15	6,3	-4,96
18	0,056	0,003	5E+3	1,25E+15	15	-5,81
15	0,067	0,00085	1E+5	6,25E+13	85	-7,07

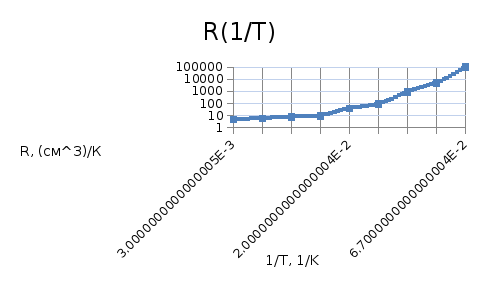
рис. 3 график зависимости постоянной Холла от температуры

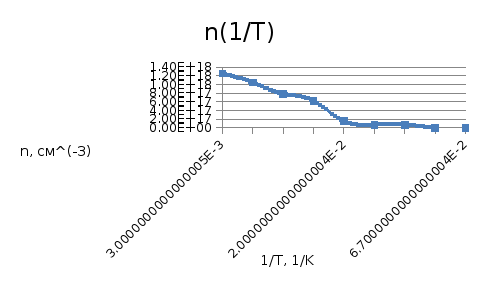
рис. 4 график зависимости концентрации от температуры

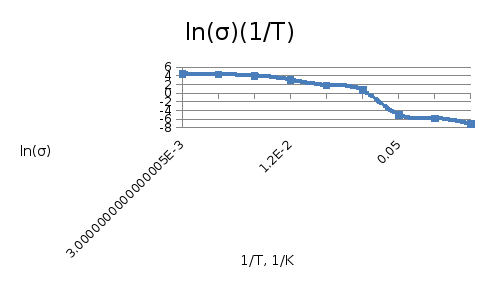
рис. 5 график зависимости электропроводности от температуры

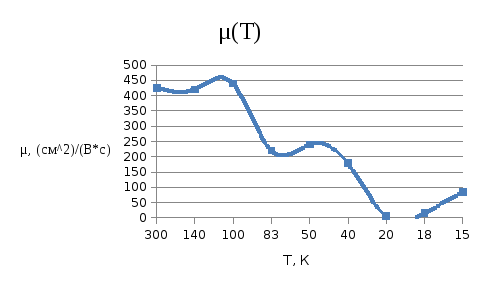
рис. 6 график зависимости подвижности от температуры