Аналітична геометрія_2011 Соколовська Г.В., Соколовський С.Ю

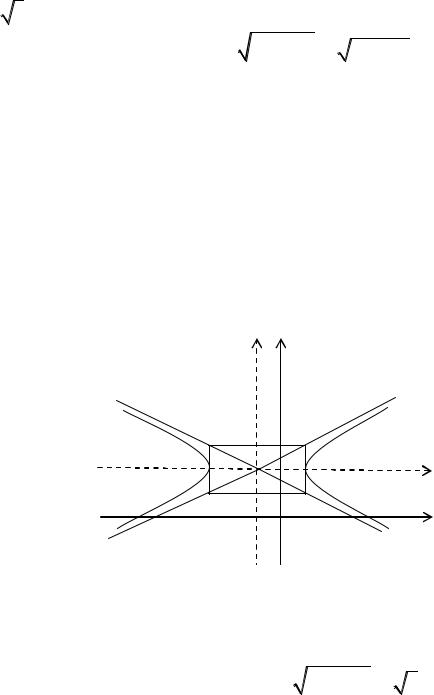
В останньому рівнянні

перейдемо до нових змінних

за

формулами

X x 1, Y y 2. Отримаємо канонічне рівняння еліпса

X 2

Y 2

1. В

12

16

системі координат xOy центр еліпса знаходиться в точці C 1; 2 , півосі

b a . Тому фокуси цього еліпса (рис.15) знахо-

a 2 3, b 4 . Як бачимо,

дяться на осі CY на відстані c b2

a2

2 від його центру.

16 12

Позначимо їх F1 та F2 .

в) x2 4y2 2x 24y 39 0 x2 2x 4 y2 6y 39 0

x 1 2 1 4 y 3 2 9 39 0 x 1 2 4 y 3 2 4

x 1 2

y 3 2

4

1

1.

X x 1,

В останньому рівнянні перейдемо до нових змінних за формулами

Y y 3. Отримаємо канонічне рівняння гіперболи

X 2

Y 2

1.

4

1

Y

y

1

-2

2

C

3

X

-1

-1

0

x

Рис. 16

xOy

В системі координат

центром гіперболи є точка C 1;3 , півосі

a 2, b 1. Вершини гіперболи знаходяться на осі CX .

Фокуси F1 та F2

знаходяться на цій же осі на відстані c

a2 b2

від центру. Гіпербо-

5

лу зображено на рис.16.

г) 16x2 9 y2 18y 135 0 16x2 9 y2 2 y 135 0

16x2 9 y 1 2

1 135 16x2 9 y 1 2

144

x2

y 1 2 1.

9

16

x, Y y 1. Отримаємо

Перейдемо до нових змінних за формулами X

канонічне рівняння гіперболи

X 2

Y 2

1. В

системі координат xOy

9

16

центром гіперболи є точка C 0; 1 ,

півосі a 3, b 4. Зробимо креслення

(рис.17).

Y

y

4

x

-3

C

0 3

X

-4

Рис. 17

Фокуси гіперболи F1,

F2 та її вершини знаходяться на осі CY . Відстань від

a2 b2

центру до фокуса c

9 16 5.

дяться на відстані

p 2 від фокуса, належать параболі (адже відстань від ко-

жної з них до фокуса та до директриси однакова).

y

Y

A F B

X

5

C

0

3

x

Рис. 18

2

е) Рівняння

x 3

8 2 y y2 задає лінію, точки x; y

якої мають

3

задовольняти умови

x 3 0,

27

8 2 y y2 0.

Піднесемо до квадрату обидві частини рівняння. Одержимо

x 3 2

4

8 2 y y2

x 3 2

4

y2 2 y 8 0

9

9

x 3 2

4

y 1 2 9 0 x 3 2

4

y 1 2

4

9

9

x 3 2

y 1 2

Y y 1, отримаємо кано-

4

9

1. Після заміни X x 3,

нічне рівняння еліпса

X 2

Y 2

1.

4

9

Але

не всі

точки

еліпса

належать

лінії,

що

задана

рівнянням

2

а лише ті, що задовольняють умови

. Зауважи-

x 3

8 2 y y2 ,

27

3

мо, що

умова

8 2 y y2 0

виконана

для

всіх

точок

еліпса, адже

Точка C 1;3 - вершина параболи,

p 8 , CF CK

p

4

. Враховую-

2

чи умови 28 або

X 0,

, одержимо тільки нижню відносно осі CX поло-

б) гіпербола має спільні фокуси з еліпсом

x2

y2

1, а її ексцентриситет

1, 25.

24

49

дикулярно векторові n A; B;C (

його називають нормальним вектором

площини)

A x x0

B y y0

C z z0 0 .

29

3.

Рівняння площини, яка проходить через 3 задані точки M1 x1; y1; z1 ,

M2 x2 ; y2 ; z2 , M3 x3; y3; z3

x x1

y y1

z z1

31

x2 x1

y2 y1

z2 z1

0 .

x3 x1

y3 y1

z3 z1

M1 a; 0; 0 ,

4.

Рівняння площини,

яка

проходить через точки

M2 0; b; 0 , M3 0; 0; c , або рівняння «у відрізках»

x

y

z

1.

32

a

b

c

M0 x0 ; y0 ; z0 паралельно векторові

s m;n; p

( його називають на-

прямним вектором прямої)

x x0

y y0

z z0

.

34

m

n

p

3. Якщо в рівняннях 34 позначити через t коефіцієнт пропорційності,

x mt x0 ,

y nt y0 ,

z pt z0 .

35

4. Рівняння прямої, що проходить через 2 задані точки M0 x0 ; y0 ; z0 ,

M1 x1; y1; z1

x x0

y y0

z z0

.

36

y

x

x

y

z

z

1

0

1

0

1

0

§ 2 Основні формули

1. Кут між двома площинами

Один з лінійних кутів між площинами P

: A x B y C z D 0 та

1

1

1

1

1

P2 : A2 x B2 y C2 z D2 0 дорівнює куту між їх нормальними вектора-

ми n1 A1 ; B1;C1 та n2

A2 ; B2;C2 . Тому

n1

n2

A1A2 B1B2

C1C2

. 37

cos P ,P

cos

1 2

n1, n2

n1

n2

2

2

2

2

2

2

A1 B1

C1

A2

B2

C2

2. Кут між двома прямими. Умови паралельності і перпендикулярності

Кут між двома прямими l

:

x x1

y y1

z z1

та

1

m1

n1

p1

x x2

y y2

z z2

l

:

визначається як кут між їх напрямними векто-

2

m2

n2

p2

рами s1

m1 ;n1; p1 та s2

m2 ;n2; p2 за формулою

s1

s2

m1m2 n1n2 p1 p2

. 38

cos l

,l

cos

1

2

s1, s2

s1

s2

m

2

n

2

p

2

m

2

n

2

p

2

1

1

1

2

2

2

l

l

s

s

m1

n1

p1

.

39

1

2

1

2

m2

n2

p2

Кут між прямою l :

x x0

y y0

z z0

та площиною

m

n

p

P : Ax By Cz D 0 визначається за формулою

s n

Am Bn Cp

sin

cos

.

41

l , P

s, n

s

n

m

2

n

2

p

2

2

2

C

2

A B

Умовою паралельності прямої і площини є ортогональність напрямного

вектора прямої і нормального вектора площини

l

P s n s n 0 Am Bn Cp 0.

42

Умовою перпендикулярності прямої і площини є колінеарність напрям-

ного вектора прямої і нормального вектора площини

l P s n

A

B

C

.

43

m

n

p

4. Відстань від точки до площини

M0 x0 ;

y0 ; z0

Відстань

d

від

точки

до

площини

Ax By Cz D 0 обчислюється за формулою

d

Ax0 By0

Cz0 D

44

.

A2 B2 C2

§3 Приклади і вправи

Вправа 3.1. Записати рівняння площини, що проходить через точку

M0 1; 5; 2

перпендикулярно осі Oy .

таємось рівнянням 29 . Отримаємо

0 x 1 1 y 5 0 z 2 0

або y 5 0 .

M0 4; 0;1 і паралельна двом

векторам a 2i 3 j та a i 3 j 2k .

Розв’язання.

i

j

k

Обчислимо векторний добуток a b

2

3

0

6i 4 j 3k . Век-

1

3

2

n 6;4;3

і точку

M0 4; 0;1 , через яку вона проходить, скориставшись

рівнянням

29 ,

отримаємо 6 x 4 4 y 0 3 z 1 0 або

6x 4 y 3z 21 0 .

Вправа 3.3. Записати рівняння площини, що проходить через точку

M0 2; 1;1 перпендикулярно до двох площин 2x z 1 0

та y 0.

Розв’язання.

Нормальні вектори заданих площин n1 2;0; 1 та n2

0;1;0 пара-

i

j

k

ком. Тобто n n1 n2 2

0

1 i 2k . Скористаємось рівнянням 29 ,

Вправа 3.4.

Вершини тетраедра знаходяться в

точках A 2;3;1 ,

B 4; 1; 2 , C 6;3;7 , D 5; 4;8 . Знайти довжину його висоти опущеної

з вершини D .

Розв’язання.

Запишемо рівняння площини, в якій лежить основа тетраедра - ABC .

Скориставшись рівнянням

31 площини,

яка проходить через три точки

A, B і C . Одержимо

x 2

y 3

z 1

x 2

y 3

z 1

4 2

1 3

2 1

0 або

2

2

3

0

6 2

3 3

7 1

4

0

6

Знайдемо, довжину висоти тетраедра як відстань d від точки D до цієї пло-

щини за формулою 44 .

d

3 5 6 4 2 8 22

77

11.

32 62 2 2

49

Вправа 3.5. Знайти кут між площиною P

:x y 2 0 та площиною

1

P2 , що відтинає на координатних осях відрізки a 3, b 2, c 1.