ИСТОРИЯ И ВЫВОД ФОРМУЛЫ,
ОПРЕДЕЛЯЮЩЕЙ ПРОПУСКНУЮ
СПОСОБНОСТЬ ГАУССОВСКОГО
КАНАЛА СВЯЗИ.
(1948 К. ШЕННОН, Н. ВИНЕР
1949 В. ТАЛЛЕР)
ВВЕДЕНИЕ
Исторический процесс инженерной разработки телекоммуникационных систем — семафорного (оптического) телеграфа, электрического телеграфа, телефона и систем радиосвязи — на определенном этапе своего развития вызвал практическую потребность в теоретическом оценивании эксплуатационно-технических характеристик различных средств электросвязи с точки зрения эффективного использования их технических параметров.
ВВЕДЕНИЕ
•Поскольку при анализе информационной пропускной способности систем электросвязи в рассмотрение включается такой многозначный термин, как «информация», история развития теории оценивания пропускной способности каналов электросвязи является довольно сложной. Необходимо придерживаться объективной точки зрения и рассмотреть развитие проблемы оценивания информационной пропускной способности каналов электросвязи (являющейся одной из важнейших прикладных задач теории информации) не с позиций сегодняшнего дня, а строго исторически, по основным первоисточникам.
ИСТОРИЯ РАЗВИТИЯ
•В течение конца 1920-х гг. Гарри Найквист и Ральф Хартли разработали фундаментальные идеи, связанные с передачей информации, с помощью телеграфа как системы коммуникаций. В то время, это был прорыв, но науки об информации и коммуникации как таковой не существовало.
КРИТЕРИЙ НАЙКВИСТА
• В 1927 году Гарри Найквист (1889-
1976) установил, что число
независимых импульсов в единицу времени, которые могут быть переданы через телеграфный канал, ограничено удвоенной максимальной
частотой пропускания канала
• где — частота импульса (имп/с), и — 
полоса пропускания (Гц)
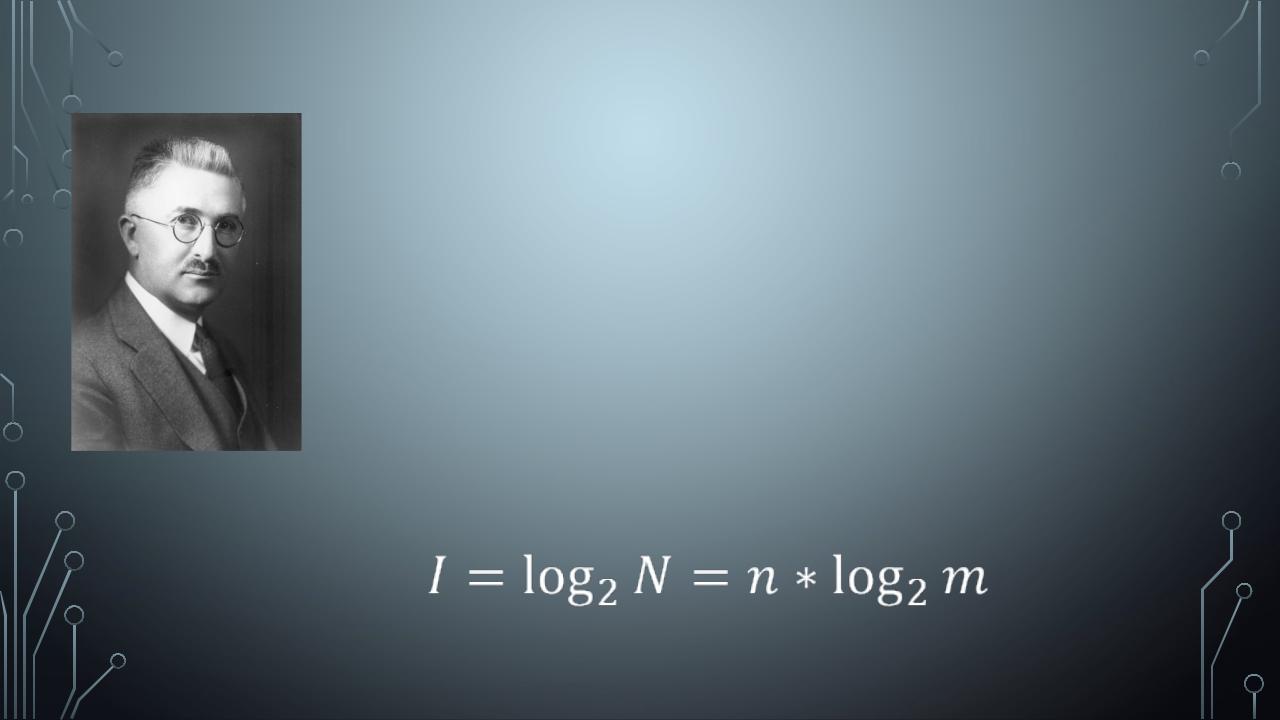
ФОРМУЛА ХАРТЛИ
•Была предложена Ральфом Хартли (1888-1970) в 1928 году как один из научных подходов к оценке
сообщений и определяет количество информации, содержащееся в сообщении длины n. 
•где N — возможное количество различных сообщений, m — количество букв в алфавите, n — количество букв в сообщении.
•Формула Хартли определяется:
ПРИМЕР
•Алфавит состоит из двух букв «B» и «X», длина сообщения 3 буквы — таким образом, m = 2, n = 3. При выбранных нами алфавите и длине сообщения можно составить разных сообщений: «BBB», «BBX», «BXB», «BXX», «XBB», «XBX», «XXB», «XXX» — других вариантов нет.
N=8 – общее количество элементов
Количество информации I, необходимой для определения конкретного элемента, есть логарифм по основанию 2 общего количества элементов N:
I
ТЕОРИЯ
ШЕННОНА
В 1940-х гг., Клод Шеннон ввёл понятие пропускной способности
канала, которое базировалось на идеях Найквиста и Хартли, а затем сформулировал полную теорию передачи информации.
В 1948 в фундаментальной работе «Математическая теория информации» Шеннон использовал инструменты теории вероятностей, разработанные Н. Винером, которые находились в зарождающейся стадии относительно их применения к теории связи в то время. Также Шеннон ввёл важное определение энтропии как меры неопределённости информации в сообщениях. Эта статья по сути положила начало такой науке, как теория информации.
КЛОД ШЕННОН (1916-2001)
Американский инженер, криптоаналитик и математик, «отец информационного века»
. Является основателем теории информации, нашедшей применение в современных высокотехнологических системах связи. Предоставил фундаментальные понятия, идеи, которые
внастоящее время формируют основу для современных коммуникационных технологий. Шеннон внёс ключевой вклад
втеорию вероятностных схем, теорию игр, 
теорию автоматов и теорию систем управления — области наук, входящие в понятие «кибернетика».
СКОРОСТЬ ПЕРЕДАЧИ И ПРОПУСКНАЯ СПОСОБНОСТЬ
•Cкорость передачи информации - количество информации, передаваемое в единицу времени. Эта величина определяется по формуле
Где - априорная и апостериорная энтропии на один символ
Для более наглядного представления о величине R укажем, что темп обычной речи соответствует скорости порядка 20 бит/с.