
2019-RG-math-Vinogradov-translation
.pdf31
Chapter 6. The method of "transferring of boundary conditions" (step-by-step version of the method) for solving boundary value problems with stiff ordinary differential equations.
6.1. The method of "transfer of boundary value conditions" to any point of the interval of integration.
The complete solution of the system of differential equations has the form
Y (x) K (x x0 )Y (x0 ) Y (x
Or you can write:
Y (0) K(0 x )Y (x ) Y |
|
(0 |
|
|
|
||||
1 |
1 |
|
|
|
x0 ) .
x1 ) .
We substitute this expression for Y (0) |
into the boundary conditions of the left edge and |
obtain:
UY (0) u , |
|
|
|
|
||
U[K (0 x1 )Y (x1 ) Y |
|
(0 |
x1 )] u , |
|||
|
||||||
UK(0 x1 )Y (x1 ) u UY |
|
(0 |
x1 ) . |
|||
|
||||||
Or we get the boundary conditions transferred to the point x1 :
U1Y (x1 ) u1 ,
where
point
U1 UK(0 x1 ) |
and |
u1 |
Further, we write similarly |
|
|
|
Y (x ) K(x |
|
|
1 |
1 |
And substitute this expression for
x1 :
u UY |
|
(0 |
x1 ) . |
|
x |
)Y (x |
|
(x |
x |
) |
) Y |
|||||
2 |
2 |
|
1 |
2 |
|
Y (x1 ) into the transferred boundary conditions of the
U1Y (x1 ) u1 ,
32
U |
|
[K(x |
x |
)Y (x |
) Y |
|
(x |
x |
)] |
|||||
|
|
|||||||||||||
1 |
|
1 |
|
2 |
|
2 |
|
|
1 |
|
|
2 |
|
|
U |
K(x |
x |
)Y (x |
) u |
U Y |
|
(x |
|
||||||
|
||||||||||||||
1 |
|
1 |
|
2 |
|
2 |
|
1 |
|
1 |
|
|
1 |
|
Or we get the boundary conditions transferred to the point
u1 |
, |
x2 ) . |
|
x2 : |
|
where
U |
2 |
U |
K(x |
x |
) |
|
1 |
1 |
2 |
|
and
U Y |
||
|
|
2 |
u |
2 |
|
|
|
|
(x |
2 |
) |
|
|
|
u |
|
|
1 |
|
|
u2 U1Y
,
(x1
x |
2 |
) |
|
|
.
And so we transfer the matrix boundary condition from the left edge to the point in the same way transfer the matrix boundary condition from the right edge.
Let us show the steps of transferring the boundary conditions of the right edge. We can write:
x |
|
|
and
Y (1) K (1 x |
|
)Y (x |
|
) Y |
|
(1 |
x |
|
) |
|
n 1 |
n 1 |
|
n 1 |
|||||||
|
|
|
|
|
|
|
|
|||
We substitute this expression for Y (1) |
in the boundary conditions of the right edge and |
|||||||||
obtain:
|
|
|
|
VY (1) v , |
|
|
|
|
|
|
|
|
|
||||
V[K (1 x |
n 1 |
)Y (x |
n 1 |
) Y (1 x |
n 1 |
)] v |
, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
VK (1 x |
|
|
)Y (x |
|
|
) v VY |
|
(1 |
x |
|
) |
|
|
|
|||
n 1 |
n 1 |
|
n 1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Or we get the boundary conditions of the right edge, transferred to the point |
xn 1 |
: |
|||||||||||||||
|
|
Vn 1Y (xn 1 ) vn 1 , |
|
|
|
|
|
|
|
|
|
||||||
where
V |
VK(1 x |
n 1 |
) |
and |
v |
n 1 |
v VY (1 x |
n 1 |
) . |
n 1 |
|
|
|
|
|
|
Further, we write similarly
Y (x |
|
) K (x |
|
x |
|
)Y (x |
|
) Y |
|
(x |
|
x |
|
) |
n 1 |
n 1 |
n 2 |
n 2 |
|
n 1 |
n 2 |
||||||||
|
|
|
|
|
|
|
|
|
And substitute this expression for Y (xn 1 ) in the transferred boundary conditions of the
point xn 1 :
Vn 1Y (xn 1 ) vn 1 ,

33
V |
|
|
[K (x |
|
|
x |
|
|
)Y (x |
|
|
) Y |
|
(x |
|
|
x |
|
|
)] v |
|
||||||
n 1 |
n 1 |
n 2 |
n 2 |
|
n 1 |
n 2 |
n 1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
V |
n 1 |
K (x |
n 1 |
x |
n 2 |
)Y (x |
n 2 |
) v |
n 1 |
V |
Y (x |
n 1 |
x |
n 2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
||||||||||||
Or we get the boundary conditions transferred to the point |
xn 2 |
: |
,
) .
|
|
|
Vn 2Y (xn 2 ) vn 2 |
, |
|
|
|
|
where |
Vn 2 Vn 1 K(xn 1 xn 2 ) |
|
and |
vn 2 vn 1 |
Vn 1Y |
|
(xn 1 |
xn 2 ) . |
|
|
|||||||
|
And so at the inner point x |
|
of the integration interval we transfer the matrix boundary |
|||||
|
|
|||||||
condition, as shown, and from the left edge and in the same way transfer the matrix boundary condition from the right edge and obtain:
|
|
) |
U Y (x |
||
V Y (x )
u
v
,
.
From these two matrix equations with rectangular horizontal coefficient matrices, we obviously obtain one system of linear algebraic equations with a square matrix of coefficients:
U |
|
|
|
|
) |
||
V |
|
Y (x |
|
|
|
||
|
|
|
6.2. The case of "stiff" differential equations.
u v

 .
.
In the case of "stiff" differential equations, it is proposed to apply a line orthonormalization of the matrix boundary conditions in the process of their transfer to the point under consideration. For this, the orthonormalization formulas for systems of linear algebraic equations can be taken in [Berezin, Zhidkov].
That is, having received
U Y (x ) u |
||
1 |
1 |
1 |
we apply a line orthonormation to this group of linear algebraic equations and obtain an equivalent matrix boundary condition:

34
U |
Y (x ) |
|
|
1орто |
1 |
u1орто
.
And in this line orthonormal equation is substituted
Y (x ) K(x |
|
1 |
1 |
x |
)Y (x |
) Y |
|
(x |
|
||||
2 |
2 |
|
|
1 |
x |
2 |
) |
|
|
.
And we get
U |
|
[K(x |
x |
)Y (x |
) Y |
|
(x |
1орто |
|
||||||
|
1 |
2 |
2 |
|
|
1 |
x |
2 |
)] |
|
|
u1орто
,
U |
1орто |
K(x x |
2 |
)Y (x |
2 |
) u |
U |
Y (x |
|
|
1 |
|
1орто |
|
1орто |
1 |
|||
Or we get the boundary conditions transferred to the point |
x |
||||||||
x2 ) .
2 |
: |
U Y (x |
) |
|
2 |
2 |
|
u2
,
where
U |
2 |
U |
1орто |
K (x |
x |
) |
|
|
1 |
2 |
|
and
u |
u |
U |
Y |
|
(x |
|
|||||
2 |
1орто |
|
1орто |
|
1 |
x |
2 |
) |
|
|
.
Now we apply linear orthonorming to this group of linear algebraic equations and obtain an equivalent matrix boundary condition:
U |
Y (x |
2 |
) u |
2орто |
|
2орто |
|
And so on.
And similarly we do with intermediate matrix boundary conditions carried from the right edge to the point under consideration.
As a result, we obtain a system of linear algebraic equations with a square matrix of coefficients, consisting of two independently stepwise orthonormal matrix boundary conditions, which is solved by Gauss’ method with the separation of the main element for obtaining the
solution Y (x ) at the point
x |
|
|
under consideration:
U |
|
|
|
|
u |
|
|
орто |
Y (x |
|
) |
орто |
|||
|
|
||||||
V |
|
|
v |
|
|||
|
|
|
|||||
орто |
|
|
|
орто |
|||
|
|
|
|
|
.
35
6.3. Formulas for computing the vector of a particular solution of inhomogeneous system of
differential equations.
Instead of the formula for computing the vector of a particular solution of an inhomogeneous system of differential equations in the form [Gantmaher]:
|
|
|
|
x |
|
|
Y |
|
(x x0 ) e |
Ax |
e |
At |
F (t)dt |
|
|
|
||||
|
|
|
|
x0 |
|
|
it is proposed to use the following formula for each individual section of the integration interval:
|
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
Y |
|
(x j |
xi ) Y |
|
(x j |
xi ) K (x j |
xi ) K (xi |
t)F (t)dt |
|
|
|
||||||||
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
The correctness of the above formula is confirmed by the following:
.
|
|
|
|
|
|
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
(x j |
xi ) exp( A(x j xi )) exp( A(xi |
t))F (t)dt |
||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
(x j |
xi ) |
exp( A(x j xi )) exp( A(xi |
t))F (t)dt |
|||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
(x j xi ) |
|
exp( A(x j |
xi |
xi t))F (t)dt , |
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x j |
|
|
|
|
|
|
|
|
|
|
Y (x j |
xi ) exp( A(x j |
t))F (t)dt , |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
(x j xi ) exp( Ax j ) |
|
exp( At)F (t)dt , |
|||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x
Y (x xi ) exp( Ax) exp( At)F (t)dt ,
,
,
xi

36
which was to be confirmed.
The calculation of the vector of a particular solution of a system of differential equations is performed using the representation of Cauchy’s matrix under the integral sign in the form of a series and integrating this series elementwise:
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
(x j |
xi ) Y |
|
(x j xi ) K (x j |
xi ) |
K (xi t)F (t)dt |
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K (x j |
|
|
|
t) A |
|
(xi t) |
|
/ 2!...)F (t)dt |
|
|
|
|
||||||||||
xi ) (E A(xi |
2 |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
j |
|
x |
j |
|
|
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
K (x j |
xi )(E F (t)dt A (xi |
t)F (t)dt A |
2 |
/ 2! (xi |
t) |
2 |
F (t)dt |
...). |
||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x |
i |
|
x |
i |
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
This formula is valid for the case of a system of differential equations with constant |
||||||||||||||||||||||
coefficient matrix |
A |
=const. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Let us consider the variant, |
when the |
steps |
|
of the |
integration |
interval |
are chosen |
|||||||||||||||
sufficiently small, which allows us to consider the vector F (t) in the region
(x |
j |
x |
) |
|
i |
|
approximately as a constant
F (x |
) constant |
i |
|
, which allows us to remove this vector from the
signs of the integrals:
|
|
|
|
x |
j |
x |
j |
|
|
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Y |
|
(x j |
xi ) K (x j |
xi )(E dt A (xi |
t)dt A |
2 |
/ 2! |
(xi |
t) |
2 |
dt |
...)F (t). |
||||||
|
|
|
||||||||||||||||
|
|
|
|
x |
i |
x |
i |
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
It is known that when T=(at+b) we have Tn dt |
|
|
1 |
|
Tn 1 |
const |
(при n -1). |
|||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
a(n 1) |
|
|
|
|
|
||||
In our case, we have
(b - t) |
n |
dt |
1 |
(b - t) |
n 1 |
|
|||||
|
|
|
|||
|
|
|
(-1)(n |
1) |
|
const |
(при n -1). |
x j |
|
1 |
|
|
Then we obtain (xi |
t)n dt |
(xi x j )n 1 . |
||
n 1 |
||||
xi |
|
|
||
|
|
|
37
Then we obtain a series for computing the vector of a particular solution of an
inhomogeneous system of differential equations on a small section (x j xi ) :
Y |
|
(x |
|
x ) K(x |
|
x ) (E A(x |
|
x |
2 |
(x |
x |
) |
2 |
/ 3! ...) (x |
|
x ) F(x ). |
|
|
j |
j |
i |
) / 2! A |
|
j |
|||||||||||
|
|
|
i |
i |
j |
|
i |
j |
|
|
|
i |
i |
||||
For
A A(x |
) |
|
i |
i |
|
the case of differential equations with variable |
coefficients, an averaged matrix |
of the coefficients of the system of differential |
equations can be used for each |
section.
If the considered section of the integration interval is not small, then the following iterative (recurrent) formulas are proposed.
We give the formulas for computing the vector of a particular solution, for example,
|
(x |
x |
) |
Y |
|||
|
3 |
0 |
|
on the considered section
(x |
x |
) |
3 |
0 |
|
through the vectors of the particular solution
Y |
|
(x1 |
x0 ) , |
Y |
|
(x2 |
x1 ) , |
Y |
|
(x3 |
x2 ) , |
corresponding to the subsections |
||
|
|
|
||||||||||||
(x2 |
x1 ) , (x3 |
x2 ) . |
|
|
|
|
|
|
|
|||||
|
|
|
|
We have Y (x) K (x x0 )Y (x0 ) Y |
|
(x x0 ) . |
||||||||
|
|
|
|
|
||||||||||
We also have a formula for a separate subsection:
(x1
x |
0 |
) |
|
|
,
x |
j |
|
|
|
Y |
|
(x j |
|
xi ) Y |
|
(x j |
xi ) K (x j xi |
) |
|
K (xi |
t)F (t)dt . |
|
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We can write: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y (x1 ) K (x1 |
x0 )Y (x0 ) Y |
|
(x1 |
x0 ) |
, |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
Y (x2 ) |
K(x2 |
|
x1 )Y (x1 ) Y |
|
(x2 |
x1 ) . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
We substitute |
Y (x ) in Y (x |
2 |
) and get: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y (x |
) K (x |
|
x )[K (x x |
)Y (x |
) Y |
|
(x |
x |
)] Y |
|
(x |
|
x ) |
||||||||||||||||||||
2 |
|
|
2 |
||||||||||||||||||||||||||||||
2 |
|
|
|
|
1 |
|
|
|
1 |
|
0 |
|
0 |
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
1 |
||
K (x |
2 |
x )K (x x |
)Y (x |
) K (x |
2 |
x )Y (x x |
) Y (x |
2 |
x ) . |
||||||||||||||||||||||||
|
|
|
1 |
|
1 |
|
0 |
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
1 |
|||
Let us compare the expression obtained with the formula:
38
Y (x |
) K (x |
|
x |
)Y (x |
) Y |
|
(x |
|
x |
) |
2 |
|
2 |
||||||||
2 |
|
0 |
0 |
|
|
|
0 |
|
and we get, obviously, that:
K(x |
x |
) K(x |
x )K(x |
x |
) |
|
2 |
0 |
2 |
1 |
1 |
0 |
|
and for the particular vector we obtain the formula:
Y |
|
(x2 |
x0 ) K (x2 |
x1 )Y |
|
(x1 |
x0 ) Y |
|
(x2 |
x1 ) . |
||||
|
|
|
|
|||||||||||
That is, the subsector vectors Y |
|
(x1 x0 ),Y |
|
(x2 |
x1 ) are not simply add with each |
|||||||||
|
|
|
||||||||||||
other, but with the participation of Cauchy’s matrix of the subsection.
|
|
|
|
Similarly, we write down |
|
Y (x3 ) K (x3 x2 )Y (x2 ) Y |
|
(x3 |
x2 ) |
and substitute the |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
formula for Y (x2 ) |
and get: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Y (x |
) K (x |
|
|
x |
)[K (x |
|
x )K (x |
|
x |
)Y (x |
) K (x |
|
|
x )Y |
|
(x |
x |
) Y |
|
(x |
|
x )] |
||||||||||||||||||||||
3 |
2 |
|
2 |
|
|
2 |
||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
1 |
0 |
|
|
0 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
0 |
|
|
|
|
1 |
|||||||
Y |
|
(x |
|
x |
|
) K (x |
|
x |
)K (x |
|
x )K (x |
x |
)Y (x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
2 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
1 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
K (x |
|
|
x |
|
)K (x |
|
x )Y |
|
(x x |
) K (x |
|
x |
)Y |
|
(x |
|
x ) |
Y |
|
(x |
|
x |
). |
|
|
|
|
|||||||||||||||||
3 |
|
|
2 |
|
3 |
|
2 |
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
1 |
|
0 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
Comparing the expression obtained with the formula:
Y (x |
) K (x |
|
x |
)Y (x |
) Y |
|
(x |
|
x |
) |
3 |
|
3 |
||||||||
3 |
|
0 |
0 |
|
|
|
0 |
|
obviously, we get that:
K(x |
x |
) K(x |
x |
)K(x |
x )K(x |
x |
) |
|
3 |
0 |
3 |
2 |
2 |
1 |
1 |
0 |
|
and together with this we get the formula for a particular vector:
That is, in this way a particular vector is calculated - the vector of the particular solution of the inhomogeneous system of differential equations, that is, for example, a particular vector
Y |
|
(x |
|
x |
|
) |
|
|
|
|
(x |
|
|
x |
|
|
) |
|
|
|
|
|
||
|
3 |
0 |
on the considered section |
3 |
0 |
is calculated through the computed partial |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
vectors |
Y (x x ) , Y (x |
|
x |
) , Y |
(x |
|
x |
|
|
) |
corresponding to the sub-sections |
(x |
x |
|
) |
|||||||||
|
|
1 |
0 |
2 |
1 |
|
|
|
3 |
|
|
2 |
|
1 |
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
, (x2 x1 ) , (x3 x2 ) .

39
6.4. Applicable formulas for orthonormalization.
Taken from [Berezin, Zhidkov]. Let there be given a system of linear algebraic equations of order n:
A x = b .
Here, above the vectors, we draw dashes instead of their designation in boldface. We will consider the rows of the matrix A of the system as vectors:
ai =( ai1 , ai2 ,…, ain ).
We orthonormalize this system of vectors.
The first equation of the system
In doing so, we get:
A
x
= b |
we divide by |
n |
2 |
|
|
a |
|
k 1 |
1k |
|
|
.
с11
x1
+
с12
x2
+…+ с1n
xn
= |
d |
|
1
,
c1=( c11,
c12
,…, c1n ),
where
c1k
=
a |
|
1k |
|
n |
2 |
|
|
a |
|
k 1 |
1k |
|
|
, |
d |
|
1
=
b |
|
1 |
|
n |
2 |
|
|
a |
|
k 1 |
1k |
|
|
|
n |
2 |
, |
c |
|
|
1k |
|
|
k 1 |
|
|
|
=1.
The second equation of the system is replaced by:
с21
x1 |
+ с22 x2 +…+ с2n xn = d |
||||||
|
|
|
|
|
|
/ |
|
|
|
where |
c2k |
= |
c2k |
|
|
|
|
|
|
n |
|
||
|
|
|
|
|
|
/ 2 |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
2k |
|
|
|
|
|
|
|
k 1 |
|
|
/ |
|
|
|
|
|
|
|
= a2k |
-( a2 , c1) c1k , |
|||||
c2k |
|||||||
2 |
, |
c2 |
=( c21, c22 |
,…, c2n ), |
||
|
|
|
/ |
|
|
|
, |
d 2 = |
d 2 |
|
, |
|
|
n |
|
|
||||
|
|
|
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
c2k |
|
|
|
|
|
|
k 1 |
|
|
|
d 2/ = b2 -( a2 , c1) d1 .
Similarly we proceed further. The equation with the number i takes the form:
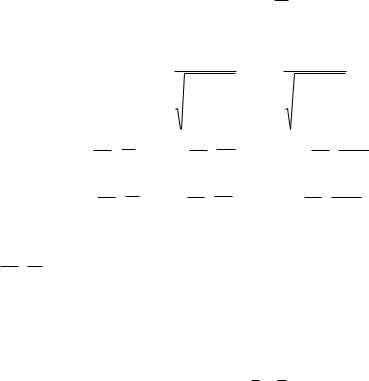
40
|
сi1 x1+ |
сi2 |
x2 +…+ |
сin xn = d i |
, |
|
|
ci |
=( ci1 |
, ci2 |
,…, cin ), |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
where |
cik |
= |
cik |
|
|
, |
d i |
= |
d i |
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ 2 |
|
|
|
|
|
|
/ 2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cik |
|
|
|
|
|
cik |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
c |
/ |
= a |
|
-( a |
|
|
, c |
|
) c |
|
|
-( a |
|
, c |
|
) c |
|
|
-…-( a |
|
, c |
i 1 |
) c |
i 1,k |
, |
|
|||||||||||||||
|
ik |
ik |
i |
|
1k |
i |
2 |
2k |
i |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
d |
/ |
= b |
-( a |
|
|
, c |
|
|
) d |
|
-( a |
|
|
, c |
|
|
) d |
|
-…-( a |
|
, c |
i 1 |
) d |
i 1 |
. |
|
|
||||||||||||
|
|
|
i |
i |
|
|
1 |
i |
2 |
2 |
i |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Here ( a |
i |
, c j |
) is the scalar multiplication of vectors. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The process will be realized if the system of linear algebraic equations is linearly |
||||||||||||||||||||||||||||||||||||||||||
independent. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As a result, |
|
we come |
|
to |
a new system |
C x d |
, where |
|
the |
matrix |
C |
will be with |
||||||||||||||||||||||||||||||
orthonormal rows, that is, it has the property
C C T
E
, where
E
is the identity matrix.
