2019-RG-math-Vinogradov-translation

11

matrix.

The matrix exponent can still be called Cauchy’s matrix and can be written as:

In the case when the system of differential equations has a matrix with variable coefficients A A(x) , the solution of Cauchy’s problem is proposed, as is known, to be sought using the property of multiplication of Cauchy’s matrices. That is, the interval of integration is divided into small sections and in small parts Cauchy’s matrix approximately calculated by the formula for the constant matrix in the exponent. And then Cauchy’s matrices calculated on small sections are multiplied:

12

Chapter 2. Improvement of S.K.Godunov’s method of orthogonal sweep for solving boundary value problems with stiff ordinary differential equations.

2.1. The formula for the beginning of the calculation by S.K.Godunov’s sweep method.

dimension 8x1, and the matrices of the boundary conditions will be rectangular horizontal dimensions 4x8.

Then in S.K.Godunov’s method for such a problem the solution is sought in the following form [Godunov]:

Y (x) Y1 (x)c1 Y2 (x)c2 Y3 (x)c3 Y4 (x)c4 Y (x) ,

or it can be written in the matrix form:

the corresponding vector of dimension 4x1 with the required constants c1 , c2 , c3 , c4 .

But in general, the solution for such a boundary-value problem with dimension 8 (outside the framework of S.K.Godunov's method) can consist not of 4 linearly independent vectors

Y1 (x),Y2 (x),Y3 (x),Y4 (x) , but entirely of all 8 linearly independent solution vectors of the

homogeneous system of differential equations:

13

Y(x) Y1 (x)c1 Y2 (x)c2 Y3 (x)c3 Y4 (x)c4

Y5 (x)c5 Y6 (x)c6 Y7 (x)c7 Y8 (x)c8 Y (x).

And just the difficulty and problem of S.K.Godunov’s method is that the solution is sought with only half the possible vectors and constants, and the problem is that such a solution with half the constants must satisfy the conditions on the left edge (the starting edge for the sweep) for all possible values of the constants, in order to find these constants from the

satisfied for any values of the constants c1 , c2 , c3 , c4 .

Usually this difficulty is "overcome" by the fact that differential equations are written not through functionals, but through physical parameters and consider the simplest conditions on the

guessed. That is, problems with complex boundary conditions can not be solved in this way: for example, problems with elastic conditions at the edges.

Below we propose a formula for the initiation of computations by S.K.Godunov’s method.

We perform the line orthonormalization of the matrix equation of the boundary conditions on the left edge:

UY (0) u , where the matrix U is rectangular and horizontal dimension 4x8.

As a result, we obtain an equivalent equation of boundary conditions on the left edge, but already with a rectangular horizontal matrix U орто of dimension 4x8, which will have 4 orthonormal rows:

How to perform line orthonormation of systems of linear algebraic equations can be found in [Berezin, Zhidkov].

We complete the rectangular horizontal matrix U орто to a square non-degenerate matrix

W :

matrix W of dimension 8х8.

As matrix M rows, we can take those boundary conditions, that is, expressions of those physical parameters that do not enter the parameters of the left edge or are linearly independent with them. This is quite possible, since for boundary value problems there are as many linearly independent physical parameters as the dimensionality of the problem, that is, in this case there are 8 of them, and if 4 are given on the left edge, then 4 can be taken from the right edge.

We complete the orthonormalization of the constructed matrix W , that is, we perform the

We can write down that

Then, substituting in the formula of S.K. Godunov’s method, we get:

Y (0) Yматрица (0)c Y (0)

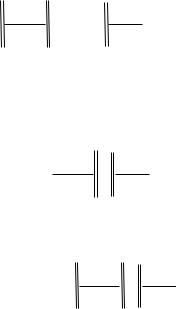
15

or

obtain:

expression:

where 0 is any vector, including a vector of zeros. Hence we obtain by means of the inverse matrix:

Then the formula for starting the computation by S.K. Godunov's method is as follows:

From the theory of matrices [Gantmakher] it is known that if the matrix is orthonormal, then its inverse matrix is its transposed matrix. Then the last formula takes the form:

2.2. The second algorithm for the beginning of the calculation by S.K.Godunov’s sweep

method.

17

2.3.The replacement of the Runge-Kutta’s numerical integration method in

S.K.Godunov’s sweep method.

In S.K.Godunov's method, as shown above, the solution is sought in the form:

At each specific section of S.K.Godunov's method of sweeping between points of orthogonalization one can use the theory of matrices instead of Runge-Kutta’s method and perform the calculation through Cauchy’s matrix:

So perform calculations faster, especially for differential equations with constant coefficients, since in the case of constant coefficients it is sufficient to calculate once Cauchy’s matrix in a small section and then only multiply by this once computed Cauchy’s matrix.

Similarly, through the theory of matrices, we can also calculate the vector Y (x) of a

particular solution of an inhomogeneous system of differential equations. Or, for this vector, Runge-Kutta’s method can be used separately, that is, one can combine the theory of matrices and Runge-Kutta’s method.

2.4 Matrix-block realizations of algorithms for starting calculation by S.K.Godunov’s

sweep method.

We consider a system of linear algebraic equations expressing the boundary conditions

for x=0

UY (0) u

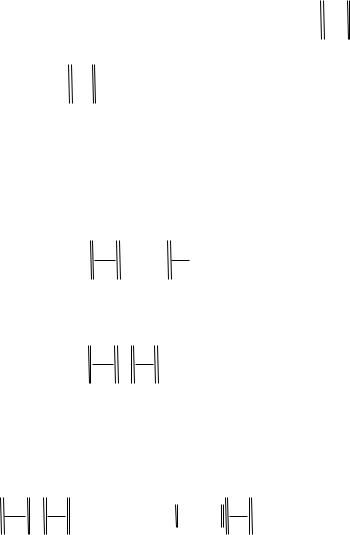
18

At the same time, we remember that the solution of the boundary value problem is sought in the form

Comparing

Another matrix derivation can be stated in the following form.

19

We transform the system

by line orthonormalization to an equivalent system with orthonormal rows

Note that another matrix-block derivation of the formulas is possible. Transition from the system

to the system

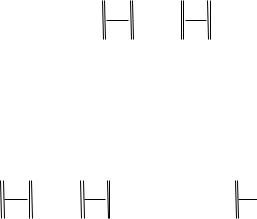
20

Then, taking into account the rule of transposition of matrices, we can write

Thus, we again obtain the orthonormal initial values of the unknown vector-valued functions of the solution.

2.5. Conjugation of parts of the integration interval for S.K.Godunov’s sweep method.

To automate the computational process on the entire integration interval, which is composed for conjugate shells with different physical and geometric parameters, the deformation of which is described by different functions, it is necessary to have the procedures of conjugation of the corresponding functions.

In the general case, the resolving functions of various parts of the integration interval of the problem have no physical meaning, and the physical parameters of the problem are expressed in various ways through these functions and their derivatives. At the same time, conjugation of adjacent sections must satisfy kinematic and force conditions at the point of conjugation.