Полученная система трёх уравнении имеет следующее решение
(4.23)
(4.24)
(4.25)
Где: (4.26)
(4.27)
(4.28)
При
этом для упрощения подставлено значение:
.
Результаты решения (4.23) - (4.28) подставляем в систему (4.1) - (4.3) и находим . Подстановкой этих параметров, а также выражений (4.23)-(4.28) в соотношения (4.17) - (4.22) завершается один шаг прогонки по элементу (i,j ).
В результате все параметры элементов будут выражены через левые боковые и верхние параметры края пластины.
Особыми случаями шагов прогонки является прохождение первых нижних и последних верхних элементов.
Для
первых нижних элементов решение уравнений
совместности деформации (4.12)-(4.14) выглядит
проще, так как условия на границе
известны.
При прохождении последних верхних элементов нет необходимости использования уравнений совместности деформаций последующих элементов, так как силовые факторы внесены в вектор параметров прогонки.
Разрешающую систему линейных алгебраических
уравнении метода механической прогонки
определяем граничными условиями для
верхнего и правого края жёстко заделанной
пластины. Это будет 6 n
уравнений
(4.29)
(4.29)
В каждое уравнение может входить 6п неизвестных, записанных в следующем порядке
(4.30)
Наиболее просто реализовать метод механической прогонки в виде программы ЭВМ с помощью трёхмерных массивов.
При
этом каждый параметр задаётся одномерным
массивом из (6n+1)
подэлементов, из которых ( 6n
) подэлементов перечисляются функциями
от аргументов в порядке (4.30), а (6n+1)
подэлемент массива определяется функцией
от F.
Этот последний подэлемент определяет
правые части линейных уравнений (4.29).
Так, как параметры в свою очередь
соответственно элементам разбиения
распределяются в двумерные массивы, то
в полной мере они характеризуются
трёхмерными массивами. Например
программная запись перемещения элемента
разбиения
будет означать перемещение сечения,
перпендикулярного к оси у, с номером i
по оси x,
с номером j
по оси у, в подэлементе, определяемом
функцией от одного из аргументов с
номером
в порядке (4.30) или F,
соответствующего номеру
Для экономии объёма памяти ЭВМ при переходе к каждому новому вертикальному столбцу элементов разбиения пластины не нужно запоминать параметры предыдущих столбцов. То есть число i можно ограничить значением: I = 2.
Отладка
программы и проверка правильности
предлагаемого метода были проведены
на примере защемлённой стальной
квадратной пластины с размерами 100х100х1
мм, нагружённой давлением: q=400
.
Известное, достаточно точное аналитическое решение, приведённое в работе [96, 97], даёт следующую формулу для прогиба в центре защемлённой пластины
(4.31)
и формулу изгибающего момента в середине края пластины отнесённого к единице длины
(4.32)
Где
;
;
.
На рисунке 4.5 даны расчётные графики распределения изгибающих моментов М по краю пластины и график распределения прогиба по пластине.
Отличие результатов численного расчёта согласно предлагаемого метода механической прогонки от результатов известных решений (4.31), (4.32) не превышает 3 - 5 % при числе участков разбиения пластины 16 – 25. Это подтверждает правильность предлагаемого метода.
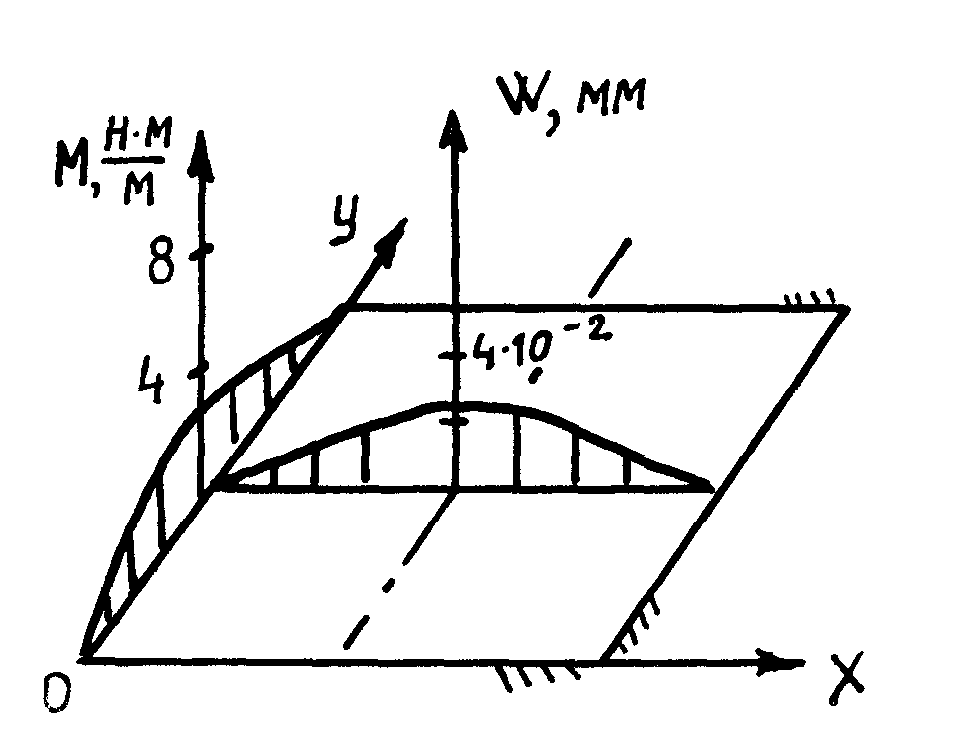
Рисунок 4.5 – Расчетные графики изменения распределенного момента М на краю пластины и прогиба W в среднем сечении пластины