2.5. Электромагнитные колебания
Формула Томсона, устанавливающая связь между периодом Т собственных колебаний в контуре индуктивностью L и электроемкостью С (активное сопротивление R = 0),
.
Дифференциальное уравнение свободных гармонических колебаний заряда в контуре и его решение:
; 
,
где qm
– амплитуда
колебаний заряда;
– собственная частота контура.
Сила тока в колебательном контуре и напряжение на конденсаторе в случае гармонических электромагнитных колебаний:
;
,
где
– амплитуда силы тока;
– амплитуда напряжения;
– собственная частота контура.
Дифференциальное уравнение свободных затухающих колебаний в контуре и его решение:
, 
,
где
– амплитуда затухающих колебаний заряда
конденсатора;
qm
– начальная амплитуда; частота
.
Добротность колебательного контура с активным сопротивлением R, индуктивностью L и электроемкостью контура C
.
Дифференциальное уравнение вынужденных электромагнитных колебаний и его решение:
, 
,
где
;
– сдвиг по
фазе между зарядом и приложенным
напряжением
;
R,
L,
C
–
соответственно
активное сопротивление, индуктивность
и электроемкость колебательного контура.
Резонансная частота и резонансная амплитуда заряда в случае электрического резонанса:
, 
,
где 0 – собственная частота контура; – коэффициент затухания; R, L, C – соответственно активное сопротивление, индуктивность и электроемкость колебательного контура; Um – амплитуда внешнего приложенного напряжения.
Резонансная частота и резонансная амплитуда силы тока в случае электрического резонанса:
, 
,
где 0 – собственная частота контура; R, L, C – соответственно активное сопротивление, индуктивность и электроемкость колебательного контура; Um – амплитуда внешнего приложенного напряжения.
2.6. Упругие и электромагнитные волны
Упругие волны
Связь длины волны с периодом Т и частотой колебаний:
; 
,
где – скорость распространения колебаний в среде (фазовая скорость).
Уравнение плоской волны, распространяющейся вдоль положительного направления оси х:
,
где
(х,
t)
– смещение
точек среды с координатой х
в момент времени t;
A
– амплитуда
волны;
– циклическая (круговая) частота;
– волновое число (
– длина волны;
– фазовая скорость; Т
– период колебаний); 0
– начальная фаза колебаний.
Связь между разностью фаз и разностью хода :
.
Условия максимума и минимума амплитуды при интерференции волн:
; 
,
где m = 0, 1, 2, … .
Фазовая и групповая u скорости, а также связь между ними:
; 
; 
.
Уравнение стоячей волны:
.
Координаты пучностей и узлов:
; 
,
где m = 0, 1, 2, … .
Уровень интенсивности звука
,
где I – интенсивность звука; I0 – интенсивность звука на пороге слышимости (I0 = 1 пВт/м2).
Скорость распространения звуковых волн в газах
,
где R – молярная газовая постоянная; М – молярная масса газа; = Ср/Сv – отношение молярных теплоемкостей газа при постоянных давлении и объеме; Т – термодинамическая температура.
Эффект Доплера в акустике:
,
где – частота звука, воспринимаемая движущимся приемником; 0 – частота звука, посылаемая источником; пр – скорость движения приемника; ист – скорость движения источника; – скорость распространения звука. Верхний знак берется, если при движении источника или приемника происходит их сближение, нижний знак – в случае их взаимного удаления.
Электромагнитные волны
Фазовая скорость распространения электромагнитных волн в среде
,
где
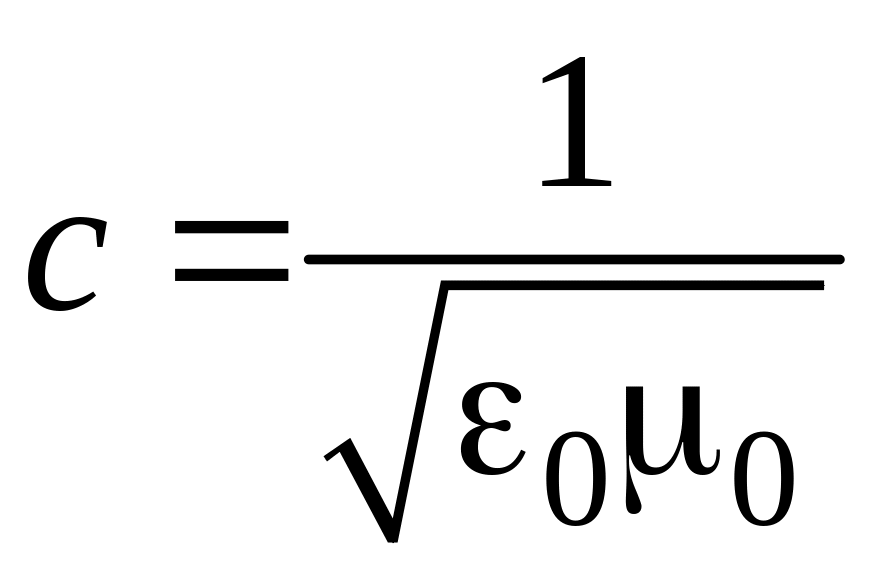– скорость распространения света в
вакууме; 0
и 0
– соответственно электрическая и
магнитная постоянные;
и
– соответственно электрическая и
магнитная проницаемости среды.
Связь между мгновенными значениями напряженностей электрического (Е) и магнитного (Н) полей электромагнитной волны:
,
где Е и Н – мгновенные значения напряженностей соответственно электрического и магнитного полей волны.
Уравнения плоской электромагнитной волны:
;
,
где
и
– амплитуды напряженностей соответственно
электрического
и
магнитного полей волны;
– круговая частота;
– волновое число;
–
начальные
фазы колебаний в точках с координатой
х
= 0.
Объемная плотность энергии электромагнитного поля
.
Плотность потока электромагнитной энергии – вектор Умова – Пойнтинга
,
где – вектор напряженности электрического поля электромагнитной волны; – вектор напряженности магнитного поля электромагнитной волны.