
- •Часть 2
- •Предисловие
- •1. Общие методические указания к решению задач и выполнению контрольных работ
- •Раздел 3. Стационарное электрическое поле
- •Раздел 4. Электромагнетизм
- •Раздел 5. Механические колебания и волны
- •Раздел 6. Электромагнитные колебания и волны
- •2. Основные законы и формулы по разделам курса физики
- •2.1. Электростатика
- •2.2. Постоянный электрический ток
- •2.3. Магнитное поле
- •2.4. Механические колебания
- •Начальная фаза результирующего колебания:
- •Период колебаний тела, подвешенного на пружине (пружинный маятник),
- •2.5. Электромагнитные колебания
- •2.6. Упругие и электромагнитные волны
2.4. Механические колебания
Уравнение гармонических колебаний
![]() ,
,
где х
– смещение
колеблющейся величины от положения
равновесия;
А
– амплитуда колебаний;
![]() – круговая (циклическая) частота;
v
= 1/Т –
частота; Т
– период колебаний; 0
– начальная фаза;
– круговая (циклическая) частота;
v
= 1/Т –
частота; Т
– период колебаний; 0
– начальная фаза;
![]() – фаза колебаний в момент t.
– фаза колебаний в момент t.
Круговая частота колебаний
![]() или
или
![]() ,
,
где и Т – частота и период колебаний.
Скорость точки, совершающей гармонические колебания,
![]() .
.
Ускорение при гармоническом колебании
![]() .
.
Амплитуда А результирующего колебания, получающегося при сложении двух гармонических колебаний одинакового направления и одинаковой частоты,
![]() .
.
Начальная фаза результирующего колебания:
 ,
,
где A1 и А2 – амплитуды двух складываемых колебаний; 1 и 2 – начальные фазы колебаний.
Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами 1 и 2,
![]() .
.
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A1 и А2 и начальными фазами 1 и 2,
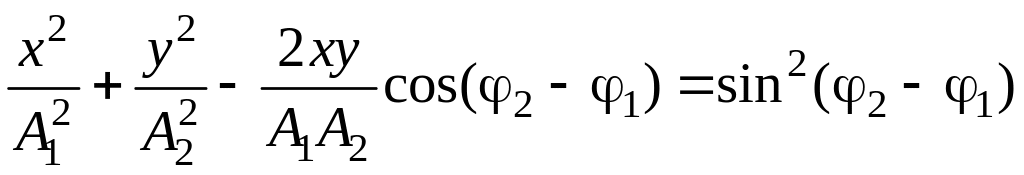 .
.
Если начальные фазы 1 и 2 составляющих колебаний одинаковы, уравнение траектории примет вид:
 ,
,
т.е. точка движется по эллипсу.
Дифференциальное уравнение гармонических колебаний материальной точки:
 , или
, или  ,
,
где m
– масса точки; k
– коэффициент квазиупругой силы (![]() ).
).
Полная энергия материальной точки, совершающей гармонические колебания,
 .
.
Период колебаний тела, подвешенного на пружине (пружинный маятник),
 ,
,
где m – масса пружинного маятника; k – жесткость пружины.
Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника
 ,
,
где l – длина маятника; g – ускорение свободного падения.
Период колебаний физического маятника
 ,
,
где J – момент инерции маятника относительно оси колебаний; а – расстояние между точкой подвеса и центром масс маятника; L = J/(mа) – приведенная длина физического маятника.
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах ~ 3 погрешность в значении периода не превышает 1 %.
Период крутильных колебаний тела, подвешенного на упругой нити,
 ,
,
где J – момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
Дифференциальное уравнение свободных затухающих колебаний:
 или
или  ,
,
где
![]() –
коэффициент затухания;
–
коэффициент затухания;
 –
собственная частота той же колебательной
системы; r
– коэффициент сопротивления.
–
собственная частота той же колебательной
системы; r
– коэффициент сопротивления.
Уравнение затухающих колебаний (решение дифференциального уравнения):
![]() ,
,
где А(t) – амплитуда затухающих колебаний в момент t; – их круговая частота.
Круговая частота затухающих колебаний
![]() .
.
Зависимость амплитуды затухающих колебаний от времени
![]() ,
,
где A0 – амплитуда колебаний в момент t = 0.
Логарифмический декремент затухания
 ,
,
где – коэффициент затухания; Т – период затухающих колебаний; – время релаксации; Ne – число колебаний, совершаемых за время уменьшения амплитуды в е раз; А(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период.
Дифференциальное уравнение вынужденных колебаний:
 ,
,  ,
,
где F0 cost – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F0 – амплитуда вынуждающей силы.
Амплитуда вынужденных колебаний
 ,
,
0 – собственная частота той же колебательной системы; – частота внешней вынуждающей силы.
Резонансная частота и резонансная амплитуда
![]() ,
,  .
.
