2.3. Магнитное поле

Механический момент, действующий на контур с током, помещенный в однородное магнитное поле,

,

где – магнитная индукция; – магнитный момент контура с током;

,

где S – площадь контура с током; – единичный вектор нормали к поверхности контура; I – сила тока.

Связь магнитной индукции и напряженности магнитного поля:

,

где – магнитная постоянная; – магнитная проницаемость среды.

Закон Био – Савара – Лапласа:

,

где – магнитная индукция поля, создаваемая элементом длины проводника с током I; – радиус-вектор, проведенный от к точке, в которой определяется магнитная индукция.

Модуль вектора

,

где  – угол между векторами и .

Принцип суперпозиции (наложения) магнитных полей:

,

где – магнитная индукция результирующего поля; – магнитные индукции складываемых полей.

Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,

,

где R – расстояние от оси проводника.

Магнитная индукция в центре кругового проводника с током

,

где R – радиус кривизны проводника.

Закон Ампера:

,

где – сила, действующая на элемент длины проводника с током I, помещенный в магнитное поле с индукцией .

Модуль силы Ампера

,

где  – угол между векторами и .

Сила взаимодействия двух прямых бесконечных прямолинейных параллельных проводников с токами I₁ и I₂

,

где R – расстояние между проводниками; dl – отрезок проводника.

Магнитная индукция поля точечного заряда Q, свободно движущегося с нерелятивистской скоростью ,

,

где – радиус-вектор, проведенный от заряда к данной точке поля.

Модуль магнитной индукции

,

где  – угол между векторами и .

Сила Лоренца

,

где – сила, действующая на заряд Q, движущийся в магнитном поле со скоростью .

Формула Лоренца:

,

где – результирующая сила, действующая на движущийся заряд Q, если на него действуют электрическое поле напряженностью и магнитное поле индукцией .

Холловская поперечная разность потенциалов

,

где B – магнитная индукция; I – сила тока; d – толщина пластинки; – постоянная Холла (n – концентрация электронов).

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора ):

,

где ₀ – магнитная постоянная; – вектор элементарной длины контура, по направлению совпадающий с обходом контура; – составляющая вектора в направлении касательной к контуру L произвольной формы (с учетом выбранного направления обхода);  – угол между векторами и ; – алгебраическая сумма токов, охватываемых контуром.

Магнитная индукция поля внутри соленоида (в вакууме), имеющего N витков,

,

где l – длина соленоида.

Магнитная индукция поля внутри тороида (в вакууме)

,

где r – радиус линии магнитной индукции внутри тороида.

Поток вектора магнитной индукции (магнитный поток) через площадку dS

,

где – вектор, модуль которого равен dS , направление совпадает с нормалью к площадке; B_n – проекция вектора на направление нормали к площадке.

Поток вектора магнитной индукции сквозь произвольную поверхность S

.

Потокосцепление (полный магнитный поток, сцепленный со всеми витками соленоида)

,

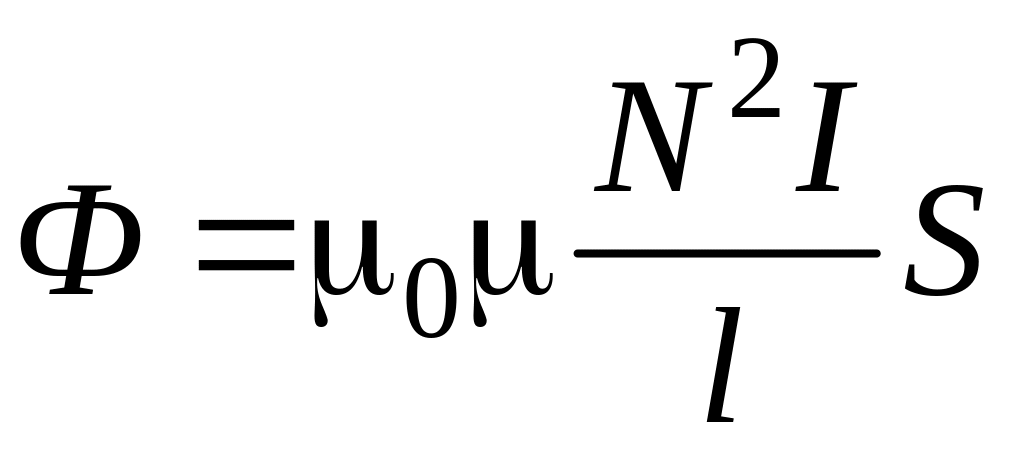где  – магнитная проницаемость среды.

Работа по перемещению проводника с током в магнитном поле

,

где dФ – магнитный поток, пересеченный движущимся проводником.

Работа по перемещению замкнутого контура с током в магнитном поле

,

где – изменение магнитного потока, сцепленного с контуром.

Закон Фарадея:

,

где – ЭДС индукции.

ЭДС индукции, возникающая в рамке площадью S при вращении рамки с угловой скоростью  в однородном магнитном поле с индукцией В,

,

где t – мгновенное значение угла между вектором и вектором нормали к плоскости рамки.

Магнитный поток, создаваемый током I в контуре с индуктивностью L,

.

ЭДС самоиндукции

,

где L – индуктивность контура.

Индуктивность соленоида

,

где N – число витков соленоида; l – его длина.

Сила тока соответственно при размыкании и замыкании цепи

и ,

где – время релаксации (L – индуктивность; R – сопротивление).

ЭДС взаимной индукции (ЭДС, индуцируемая изменением силы тока в соседнем контуре)

,

где L₁₂ – взаимная индуктивность контуров.

Взаимная индуктивность двух катушек (с числом витков N₁ и N₂), намотанных на общий тороидальный сердечник,

,

где  – магнитная проницаемость сердечника; l – длина сердечника по средней линии; S – площадь сердечника.

Коэффициент трансформации

,

где N, , I – соответственно число витков, ЭДС и сила тока в обмотках трансформатора.

Энергия магнитного поля, создаваемого током в замкнутом контуре, по которому течет ток I,

.

Объемная плотность энергии однородного магнитного поля длинного соленоида

.