3.7.4. Розв’язок завдань із застосуванням комп’ютера

Застосування системи STATISTICA

Завдання. Фірмі побутових послуг «Сонечко» необхідно розробити модель для прогнозу майбутніх обсягів послуг. На обсяги послуг фірми можуть впливати такі чинники, як: доходи населення по регіону, рівень безробіття тощо. На рис. 3.7.1 наведені дані спостережень за сімнадцять років про річні обсяги послуг фірми, доходи населення, рівень безробіття по регіону.

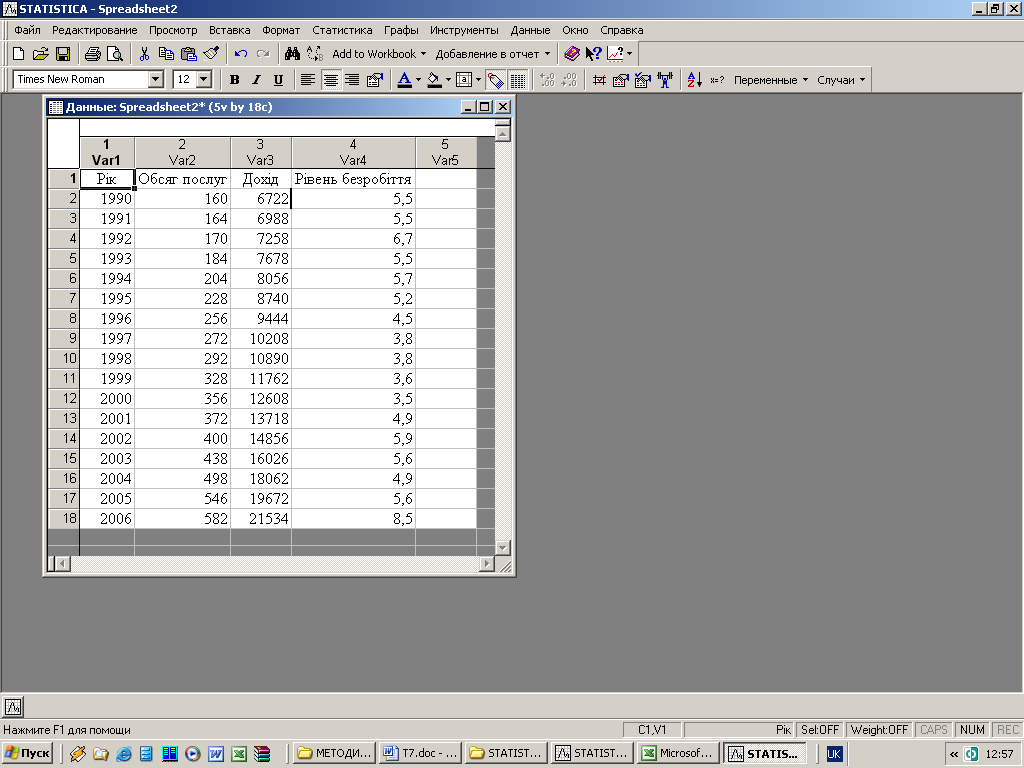
Рис. 3.7.1. Дані про річні обсяги послуг фірми «Сонечко»

Розв’язок в системі STATISTICA

Початкова модель мала вигляд , де - обсяг послуг фірми, - доходи населення даного регіону. Результати розрахунку у модулі Множественная регрессия показані на рис. 3.7.2. Перевіримо наявність в моделі серійної кореляції. Для цього у вікні Аналіз составной регрессии за допомогою кнопок Остатки, Выполнить остаточный анализ, Дарбин-Ватсон статистический знайдемо статистику Дарбіна-Уотсона. На рис. 3.7.3 показано, що оцінка DW дорівнює 0,72. Для рівня значущості , та критичні значення DW² становлять L =1,13 , U =1,38. Оскільки DW = 0,72 < L =1,13, критерій свідчить про наявність серійної кореляції. Можливо, в моделі пропущена важлива змінна, яка пояснює частину залежності між обсягом послуг у різні роки. Це припущення може бути правильним, навіть не дивлячись на те, що змінна доходів пояснює 99,5% обсягу послуг (R²).

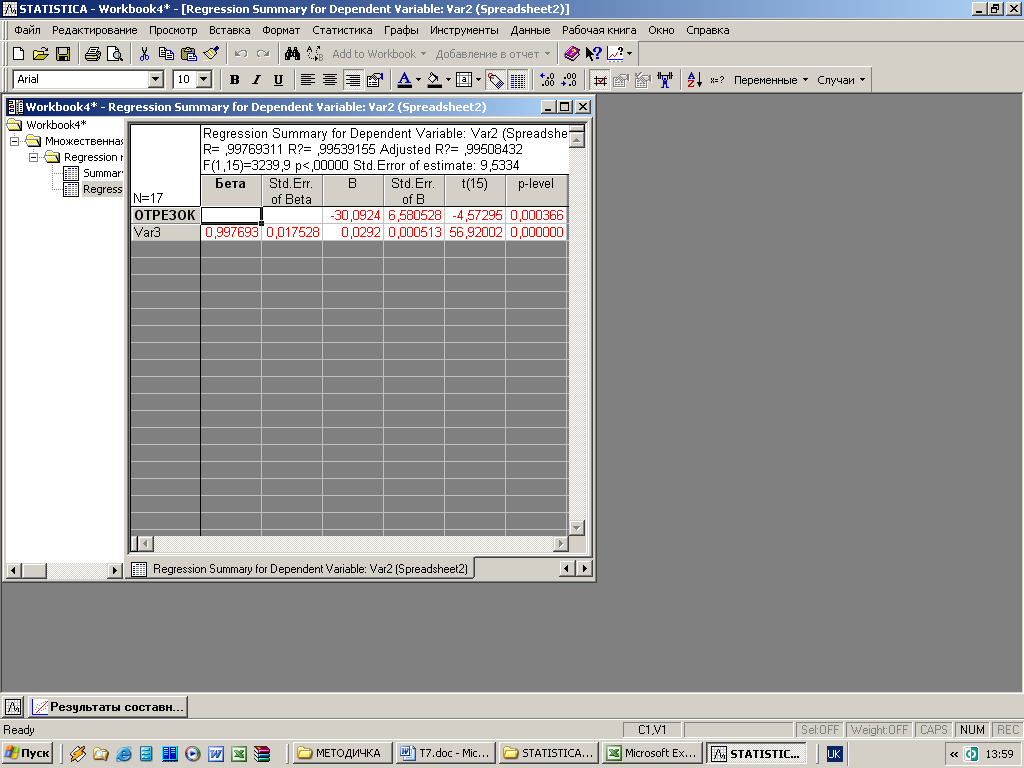
Рис. 3.7.2. Результати оцінювання парної регресії для прогнозування обсягу послуг фірми в залежності від зміни доходів населення

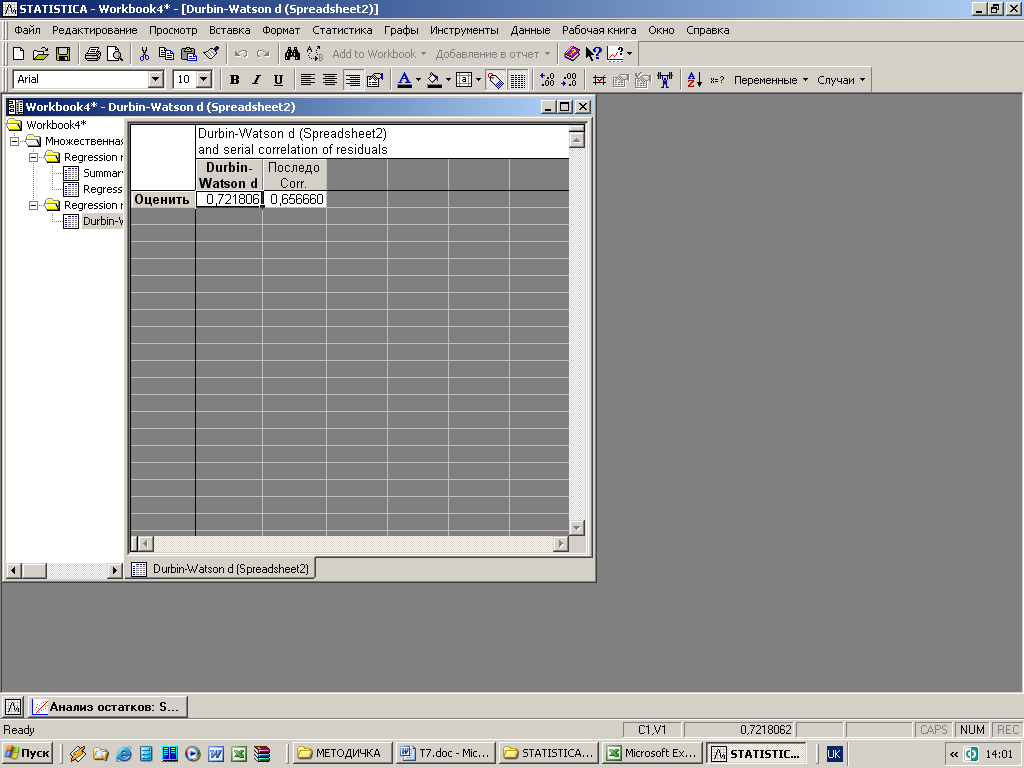
Рис. 3.7.3. Оцінка статистики Дарбіна-Уотсона

Такою важливою змінною може стати рівень безробіття по регіону. На рис. 3.7.4 наведені результати регресійного аналізу після включення в модель означеної незалежної змінної ( ).

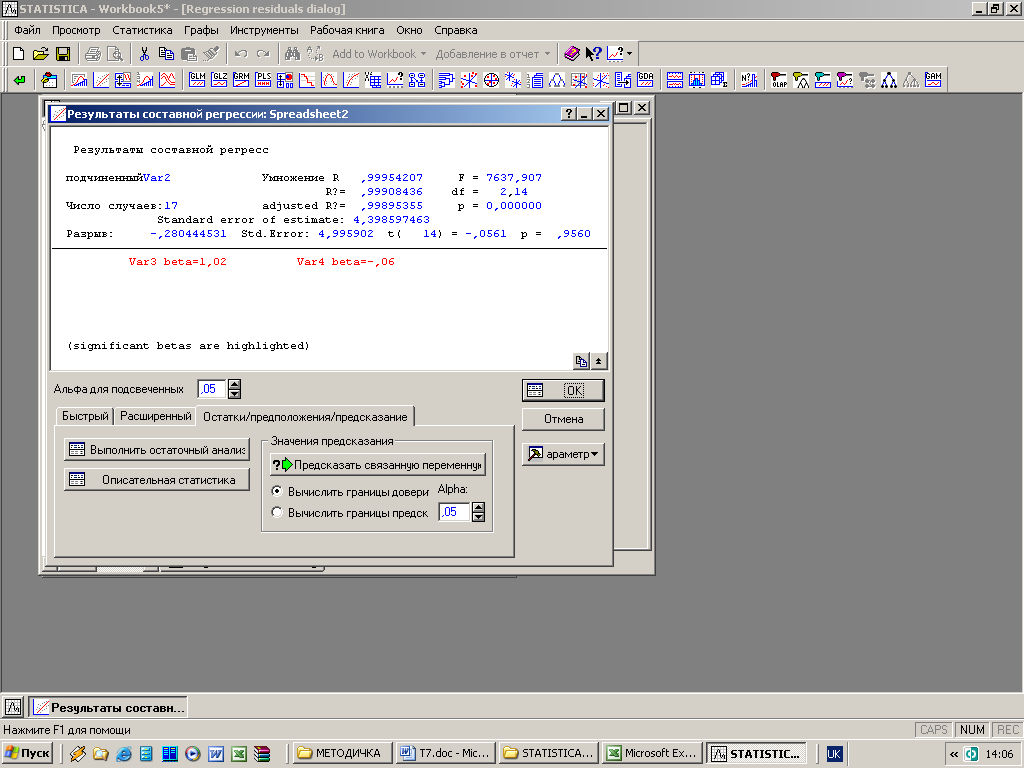Рис. 3.7.4. Результати оцінювання множинної регресії для прогнозування обсягу послуг фірми

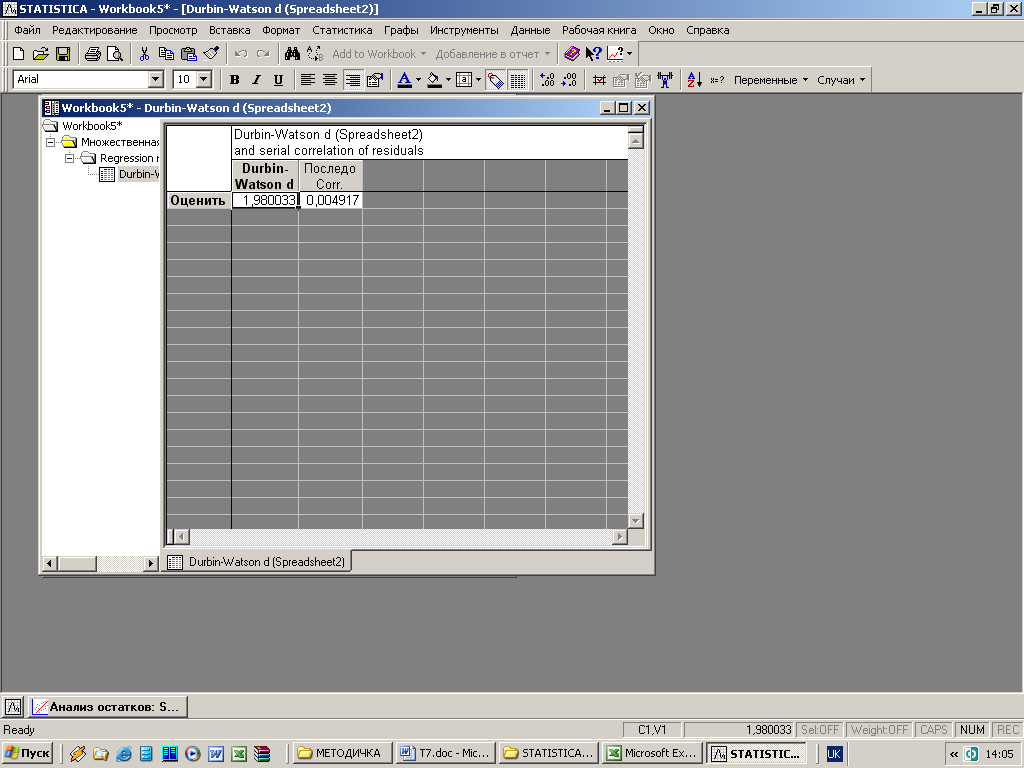
Рис. 3.7.5. Оцінка статистики Дарбіна-Уотсона для множинної регресії

Тепер у зміненій моделі статистика Дарбіна-Уотсона дорівнює 1,98. Для рівня значущості , та критичні значення DW становлять L =1,02 , U =1,54. Оскільки DW = 1,98 > U =1,54, критерій свідчить про відсутність серійної кореляції.

Для прогнозу обсягу послуг фірми «Сонечко» модель можна впевнено використовувати, оскільки параметри моделі статистично значущі і залишки незалежні.

4.7.5. Термінологічний словник

Множинна регресія – використовує більш ніж одну незалежну змінну для прогнозу значень залежної змінної.

Мультиколінеарність – це ситуація, у якій незалежні змінні у рівнянні множинної регресії корелюють між собою.

Стандартна похибка оцінювання – це стандартне відхилення залишків. Вона вимірює величину, на яку існуючі значення відрізняються від їхніх оцінок .

Покрокова регресія - це процедура вибору “кращої” функції регресії шляхом додавання або видалення окремих незалежних змінних на різних етапах аналізу.

Прогнозування поза допустимою множиною – пов’язане із додаванням нових незалежних змінних у функцію регресії. Вони повинні мати значення з тієї самої галузі, що й дані вибірки, яка була використана у аналізі.

Частковий коефіцієнт регресії вимірює середню зміну залежної змінної за одиничної зміни відповідної незалежної змінної, якщо решта незалежних змінних є сталими.