§4.Исследование системы на устойчивость по первому приближению.

Пусть дана система дифференциальных уравнений

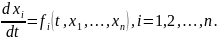(4.1)

функции имеют непрерывные производные по в окрестности начала координат до второго порядка включительно.

Разлагаем функции по формуле Тейлора в окрестности и отбрасываем слагаемые выше первого порядка относительно :

, (4.2)

Порядок 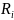выше первого относительно .

Систему (4.2) заменяем системой

(4.3)

Система (4.3) называется системой дифференциальных уравнений первого приближения для системы (4.2) (и (4.1)).

Исследуем точки покоя на устойчивость в случае, когда коэффициенты , т.е. система (4.1) стационарна в первом приближении.

Достаточные условия устойчивости и неустойчивости в первом приближении даются следующими двумя теоремами.

Теорема 1. Если система (4.1) стационарна в первом приближении и , справедливо в достаточно малой окрестности начала координат неравенство

и все корни характеристического уравнения системы (4.1) имеют отрицательные действительные части, то решение системы (4.1) асимптотически устойчиво.

Теорема 2. Если система (4.1) стационарна в первом приближении, функции , удовлетворяют условиям теоремы 1 и хотя бы один корень характеристического уравнения системы (6.1) имеет положительную действительную часть, то точка покоя системы (4.1) неустойчива.

Отметим, что теоремы 1 и 2 не охватывают лишь так называемый критический случай: все характеристические корни имеют Re , причём хотя бы для одного корня Re . В этом случае на устойчивость точки покоя системы (4.1) начинают влиять нелинейные слагаемые остаточных членов и исследование устойчивость, вообще говоря, невозможно.