
- •Тема III. Системы дифференциальных уравнений. §1. Интегрирование системы дифференциальных уравнений сведением к одному уравнению более высокого порядка.
- •§2. Системы линейных дифференциальных уравнений.
- •§3. Устойчивость по Ляпунову. Классификация точек покоя.
- •§4.Исследование системы на устойчивость по первому приближению.
§3. Устойчивость по Ляпунову. Классификация точек покоя.
Пусть некоторый процесс описывается системой дифференциальных уравнений
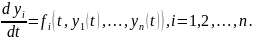 (3.1)
(3.1)
с
начальными условиями
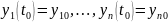 .
.
Начальные условия обычно определяются из опыта и, следовательно, неизбежно содержат некоторые погрешности.
Если бы малые изменения начальных условий сильно влияли на решение, то решение, найденное по начальным условиям, не представляло бы никакого интереса, так как даже приближённо не описывало бы изучаемый процесс.
Для прикладных задач важным является вопрос: при каких условиях достаточно малое изменение начальных значений вызывает сколь угодно малые изменения решения?
Если
рассматриваемые значения
 ,
то этим вопросом занимается теория
устойчивости.
,
то этим вопросом занимается теория
устойчивости.
Решение
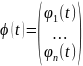 системы (3.1) называется устойчивым
по Ляпунову,
если
системы (3.1) называется устойчивым
по Ляпунову,
если
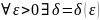 такое, что
такое, что
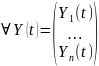 – решения (3.1) при
– решения (3.1) при
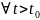 и выполняются условия
и выполняются условия
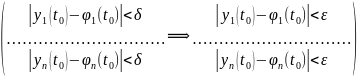 .
.
Геометрически
в случае n=2
устойчивость по Ляпунову означает, что
все решения, мало отличающиеся в начальный
момент времени
 от
от
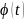 ,
не выйдут за пределы “
,
не выйдут за пределы “ -трубы”
около
в любой следующий момент времени
-трубы”
около
в любой следующий момент времени
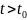 (рис 3.1).
(рис 3.1).
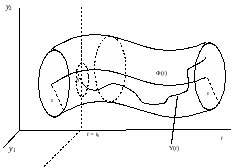
Рис 3.1.
Если
решение
системы (3.1) устойчиво по Ляпунову и
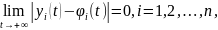 то решение
называется асимптотическим
устойчивым.
то решение
называется асимптотическим
устойчивым.
Пример 1. Исходя из определения, выяснить, устойчиво ли решение системы
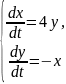
с
начальными условиями
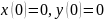 .
.
Решение. Записываем соответствующее характеристическое уравнение:
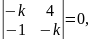
или
 .
.
Решение системы ищем в виде:

Подставляя
функции
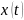 и
и
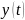 в одно из уравнений системы, например
первое, получаем
в одно из уравнений системы, например
первое, получаем
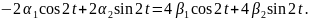
Отсюда

В векторной форме
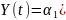
Подставляем начальные условия, тогда
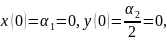
и
на устойчивость предлагается исследовать
решение
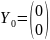 .
.
Составляем
разность
 .
При произвольном t
она имеет вид:
.
При произвольном t
она имеет вид:
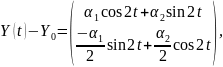
что
при t=0
обращается в вектор
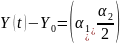 .
.
Необходимо
выяснить, каким нужно взять
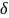 ,
чтобы из неравенств
,
чтобы из неравенств
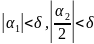 при произвольном t
следовала справедливость неравенств:
при произвольном t
следовала справедливость неравенств:
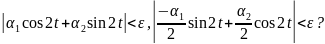
Полагаем
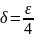 .
Тогда имеем при любом
.
Тогда имеем при любом
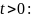
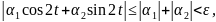
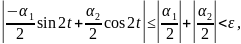
и решение устойчиво по Ляпунову.
Следует
отметить, что оно не является асимптотически
устойчивым, так как
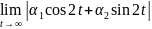 не существует.
не существует.
Исследование
на устойчивость решения системы (3.1)
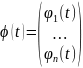 можно свести к исследованию тривиального
решения – “точки покоя”. В самом деле,
пусть
можно свести к исследованию тривиального
решения – “точки покоя”. В самом деле,
пусть
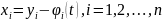 .
Тогда
.
Тогда
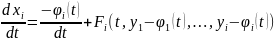 (3.2)
(3.2)
Исследовать
на устойчивость решение
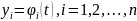 ,
системы (3.1) означает исследовать решение
,
системы (3.1) означает исследовать решение
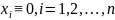 ,
системы (3.2).
,
системы (3.2).
Перефразируем
применительно к (3.2) определение
устойчивости решения по Ляпунову: точка
покоя
,
системы (3.2) называется устойчивой по
Ляпунову, если
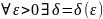 такое, что
такое, что
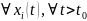 из неравенства
из неравенства
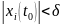 следует неравенство
следует неравенство
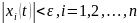 .
.
Или иначе:
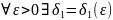 ,
что
,
что
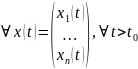 из неравенства
из неравенства
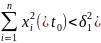 следует неравенство
следует неравенство
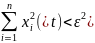 .
.
Рассмотрим различные возможности расположения траекторий в окрестности точки покоя системы двух линейных однородных дифференциальных уравнений с постоянными коэффициентами
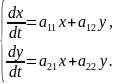 (3.3)
(3.3)
Будем
считать
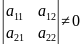 .
Решение ищем в виде
.
Решение ищем в виде
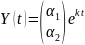 .
Характеристическое уравнение:
.
Характеристическое уравнение:
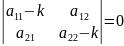 .
.
Случай
1.
Характеристические корни действительны
и различны. Пусть это числа
и
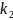 .
Тогда общее решение системы уравнений
(3.3) имеет вид:
.
Тогда общее решение системы уравнений
(3.3) имеет вид:
 (3.4)
(3.4)
Коэффициенты
 и
и
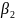 линейно выражаются через
линейно выражаются через
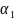 и
и
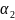 .
.
Дальнейшее описание фазовой плоскости проводим отдельно для нескольких случаев в зависимости от знаков и .
а)
Случай
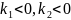 и для определённости
и для определённости
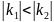 .
.
Тогда
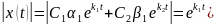
Обозначаем
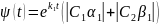 .
Функция
.
Функция
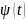 при
при
 бесконечно малая (как произведение
ограниченной функции на бесконечно
малую
бесконечно малая (как произведение
ограниченной функции на бесконечно
малую
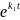 ),
тогда и
тоже бесконечно малая при
(теорема сравнения).
),
тогда и
тоже бесконечно малая при
(теорема сравнения).
Аналогично при бесконечно малая функция.
Итак,
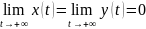 .
.
Траектории системы двух линейных однородных дифференциальных уравнений с постоянным коэффициентами (3.3) на фазовой плоскости ведут себя следующим образом:
Все
точки, находящиеся в начальный момент
времени
в произвольной -окрестности начала
координат, при достаточно большом
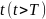 переходят в точки., лежащие в сколь
угодно малой
переходят в точки., лежащие в сколь
угодно малой
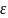 -окрестности
начала координат, а при
стремятся к началу координат.
-окрестности
начала координат, а при
стремятся к началу координат.
Точка покоя устойчива по Ляпунову и асимптотически устойчива.
Точка покоя рассмотренного типа называется устойчивым узлом.
Пример 2. Исследовать точку покоя системы дифференциальных уравнений и дать чертёж расположения траекторий на плоскости xOy.
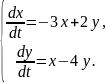
Решение. Записываем характеристическое уравнение

или
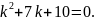
Характеристические
корни
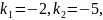 точка покоя – устойчивый узел.
точка покоя – устойчивый узел.
Переходим
от системы к уравнению
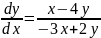 и, чтобы найти те решения, которые
изображаются прямыми, проходящими через
особую точку (0,0), подставляем в уравнение
и, чтобы найти те решения, которые
изображаются прямыми, проходящими через
особую точку (0,0), подставляем в уравнение
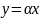 .
Получаем
.
Получаем
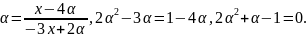
Отсюда
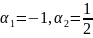 .
Получили прямые
.
Получили прямые
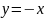 и
и
 .
.
Чтобы узнать, какой из найденных кривых касаются интегральные кривые, строим изоклины:
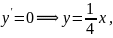
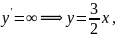

Отметим,
что интегральные кривые, попав в угол
и
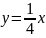 ,
не могут оттуда выйти, так как там
,
не могут оттуда выйти, так как там
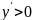 ,
поэтому интегральные кривые касаются
решения
.
,
поэтому интегральные кривые касаются
решения
.
Примерное расположение траекторий для данной системы уравнений изображено на рис. 3.2.
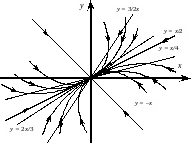
Рис 3.2.
б)
Случай
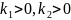 .
Заменой t
на
–t
сводим
этот случай к уже рассмотренному случаю
1а. Траектории имеют такой же вид, как в
случае 1а, однако с возрастанием
t
точки, сколь угодно близкие в начальный
момент времени
к началу координат, удаляются из
-окрестности начала координат. Точка
покоя в этом случае не является устойчивой
по Ляпунову.
.
Заменой t
на
–t
сводим
этот случай к уже рассмотренному случаю
1а. Траектории имеют такой же вид, как в
случае 1а, однако с возрастанием
t
точки, сколь угодно близкие в начальный
момент времени
к началу координат, удаляются из
-окрестности начала координат. Точка
покоя в этом случае не является устойчивой
по Ляпунову.
Точка покоя рассмотренного типа называется неустойчивым узлом.
Примерный вид траектории изображён на рисунке 3.3.
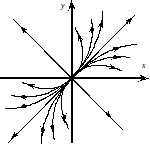
Рис 3.3.
в)
Случай
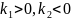 .
Из (3.4) при
.
Из (3.4) при
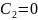 имеем
имеем
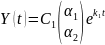 или
или
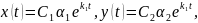 т.е. траектория удаляется от точки покоя,
а следовательно, точка покоя не является
устойчивой по Ляпунову.
т.е. траектория удаляется от точки покоя,
а следовательно, точка покоя не является
устойчивой по Ляпунову.
Исключая
из последних равенств t,
получаем
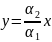 .
Другими
словами, с возрастанием t
точка удаляется от начала координат
по прямой
.
Другими
словами, с возрастанием t
точка удаляется от начала координат
по прямой
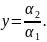
Отметим,
что существуют траектории, по которым
точки приближаются к началу координат.
В частности, при
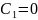
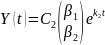 или
или
 .
Так как
.
Так как
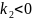 ,
то при
,
то при
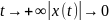 и
и
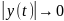 .
На фазовой плоскости это соответствует
тому, что при
точка приближается к началу координат
по прямой
.
На фазовой плоскости это соответствует
тому, что при
точка приближается к началу координат
по прямой
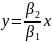 .
.
Точка покоя рассмотренного типа называется седлом.
Примерное расположение траекторий на фазовой плоскости изображено на рис 3.4.
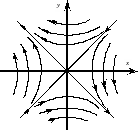
Рис 3.4.
Пример 2. Исследовать точку покоя системы
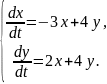
Дать чертёж расположения траекторий на плоскости xOy.
Решение. Записываем характеристическое уравнение
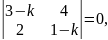
или
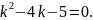
Характеристические
корни
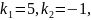 точка покоя – седло.
точка покоя – седло.
Переходим
от системы к уравнению
 , полагая в нём
.
Получаем
, полагая в нём
.
Получаем
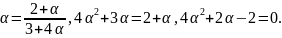
Отсюда . Прямые и изображают решения, проходящие через особую точку (0,0).
Строим изоклины:

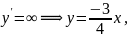
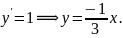
Для выяснения, какая траектория соответствует приближению к началу координат, решаем исходную систему.
Частное
решение ищем в виде
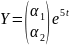 .
Подставляя его в первое уравнение
системы, находим
.
Подставляя его в первое уравнение
системы, находим
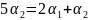 ,
откуда
,
откуда
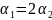 и
и
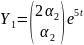 .
Аналогичным образом находим второе
частное решение
.
Аналогичным образом находим второе
частное решение
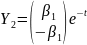 .
Фундаментальную систему составят,
например, вектор-функции
.
Фундаментальную систему составят,
например, вектор-функции
 и
и
 ,
тогда общее решение
,
тогда общее решение
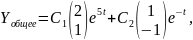
или
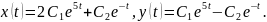
При
имеем
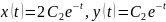 ,
отсюда
,
отсюда
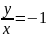 ,
при
.
,
при
.
Таким
образом, на фазовой плоскости при
точка приближается к началу координат
по прямой
(а по прямой
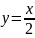 удаляется от начала координат).
удаляется от начала координат).
Расположение траекторий на фазовой плоскости изображено на рис 3.5.
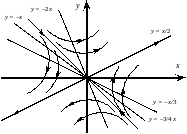
Рис 3.5.
Случай
2. Корни
характеристического уравнения
комплексные. Пусть
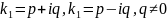 ,
тогда общее решение системы (3.3) имеет
вид:
,
тогда общее решение системы (3.3) имеет
вид:
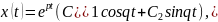
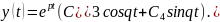
Коэффициенты
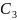 и
и
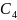 выражаются линейно через
выражаются линейно через
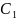 и
и
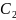 .
.
а)
Случай
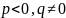 .
Тогда
.
Тогда
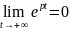 и, следовательно, функция
и, следовательно, функция
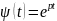 при
бесконечно малая, а так как
при
бесконечно малая, а так как
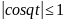 и
и
 ,
то
,
то
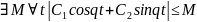 и
и
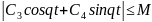 .
Отсюда следует, что
и
при
являются бесконечно малыми (как
произведение бесконечно малой функции
на ограниченную).
.
Отсюда следует, что
и
при
являются бесконечно малыми (как
произведение бесконечно малой функции
на ограниченную).
Итак, , значит, точка покоя устойчива по Ляпунову и асимптотически устойчива. На фазовой плоскости траектории асимптотически приближаются к началу координат.
б)
Случай
 .
Заменой t
на
–t
сводим
этот случай к уже рассмотренному случаю
2а. Следовательно, траектории не отличаются
от траекторий случая 2а, но движение по
ним происходит в противоположном
направлении.
.
Заменой t
на
–t
сводим
этот случай к уже рассмотренному случаю
2а. Следовательно, траектории не отличаются
от траекторий случая 2а, но движение по
ним происходит в противоположном
направлении.
Так
как
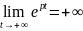 ,
то и
,
то и
 ,
и
,
и
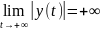 ,
и точки, находившиеся в начальный момент
времени
в сколь угодно малой окрестности начала
координат, при стремлении
удаляются к
,
и точки, находившиеся в начальный момент
времени
в сколь угодно малой окрестности начала
координат, при стремлении
удаляются к
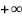 .
Точка покоя в этом случае не является
устойчивой по Ляпунову, она называется
неустойчивым
фокусом.
.
Точка покоя в этом случае не является
устойчивой по Ляпунову, она называется
неустойчивым
фокусом.
Пример 4. Исследовать точку покоя системы дифференциальных уравнений и дать чертёж расположения траекторий на плоскости xOy.
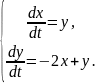
Решение. Записываем характеристическое уравнение
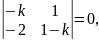
или
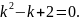
Характеристические
корни комплексно-сопряжённые:
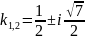 .
.
Так
как Re
 ,
то точка покоя – неустойчивый фокус.
,
то точка покоя – неустойчивый фокус.
Строим
в точке (1,0) вектор скорости
 ,
что означает, что возрастанию t
соответствует движение по часовой
стрелке. Так как фокус неустойчивый,
траектории по часовой стрелке удаляются
от начала координат.
,
что означает, что возрастанию t
соответствует движение по часовой
стрелке. Так как фокус неустойчивый,
траектории по часовой стрелке удаляются
от начала координат.
Строим изоклины:
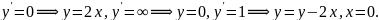
Траектории фазовой плоскости изображены на рис 3.6.

Рис 3.6.
в)
Случай
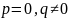 .
Общее решение имеет вид:
.
Общее решение имеет вид:
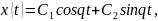
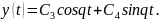
На фазовой плоскости траектории – замкнутые кривые, окружающие начало координат (0,0). Точка покоя системы называется в этом случае центром.
Центр по определению является устойчивой по Ляпунову точкой покоя, так как
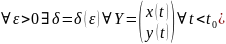
Иными
словами, замкнутые траектории, точки
которых в начальный момент времени
лежат в -окрестности начала координат,
не покидают этой
-окрестности
при
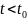 .
.
Отметим,
что асимптотической устойчивости нет,
так как
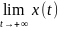 не существует.
не существует.
Примерное расположение траекторий в случае центра приведено на рис 3.7.
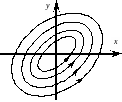
Рис 3.7.
Случай 3. Корни характеристического уравнения – кратные.
а)
Случай
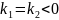 .
В этом случае характеристические корни
не могут быть комплексными, так как
комплексные корни входят в решение
характеристического уравнения
сопряжёнными парами (в силу того, что
коэффициенты уравнений в системе (3.3),
а следовательно, и характеристического
уравнения вещественны).
.
В этом случае характеристические корни
не могут быть комплексными, так как
комплексные корни входят в решение
характеристического уравнения
сопряжёнными парами (в силу того, что
коэффициенты уравнений в системе (3.3),
а следовательно, и характеристического
уравнения вещественны).
Общее решение имеет вид:
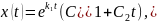
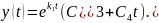
Откуда

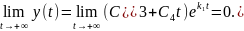
Точка покоя устойчива по Ляпунову и асимптотически устойчива, она называется, как и в случае 1а, устойчивым узлом.
Расположение траекторий на фазовой плоскости приведено на рис. 3.8.
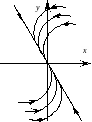
Рис 3.8.
При
 это так называемый дикритический узел
(рис 3.9).
это так называемый дикритический узел
(рис 3.9).
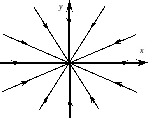
Рис 3.9.
б)
Случай
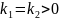 .
Заменой t
на
–t
сводим
этот случай к уже рассмотренному случаю
3а
– неустойчивый
узел (рис 3.10).
.
Заменой t
на
–t
сводим
этот случай к уже рассмотренному случаю
3а
– неустойчивый
узел (рис 3.10).
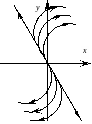
Рис 3.10
