
- •Тема III. Системы дифференциальных уравнений. §1. Интегрирование системы дифференциальных уравнений сведением к одному уравнению более высокого порядка.
- •§2. Системы линейных дифференциальных уравнений.
- •§3. Устойчивость по Ляпунову. Классификация точек покоя.
- •§4.Исследование системы на устойчивость по первому приближению.
Тема III. Системы дифференциальных уравнений. §1. Интегрирование системы дифференциальных уравнений сведением к одному уравнению более высокого порядка.
Пусть дана система дифференциальных уравнений
 (1.1)
(1.1)
Решением
системы (1.1) называется n-мерная
вектор-функция
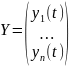 ,
при подстановке компонент которой в
(1.1) получается n тождеств.
,
при подстановке компонент которой в
(1.1) получается n тождеств.
Одним из самых распространённых методов решения системы (1.1) является метод сведения её к одному уравнению более высокого порядка. Заключается он в следующем: из уравнений системы (1.1) и уравнений, получающихся дифференцированием уравнений, входящих в (1.1), исключают все неизвестные компоненты вектор-функции, кроме одной, для нахождения которой получают тем самым одно дифференциальное уравнение более высокого порядка. Путём интегрирования полученного уравнения находят одну из компонент искомого решения системы. Затем, используя уравнения системы (1.1) и уравнения, полученные при поиске одной компоненты, находят остальные компоненты решения.
Пример 1. Проинтегрировать сведением к одному уравнению систему
 (1.2)
(1.2)
Решение. Дифференцируем второе уравнение:
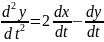 . (1.3)
. (1.3)
Подставляем
 из первого уравнения системы (1.2) в (1.3):
из первого уравнения системы (1.2) в (1.3):
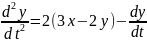 ,
,
или
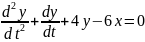 . (1.4)
. (1.4)
Из второго уравнения системы (1.2) находим x
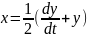 (1.5)
(1.5)
и, подставляя его в уравнение (1.4), получаем
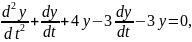
или
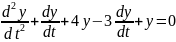 . (1.6)
. (1.6)
Уравнение (1.6) является линейным однородным уравнением второго порядка с постоянным коэффициентами. Соответствующее ему характеристическое уравнение:

Следовательно, решение этого однородного уравнения имеет вид:
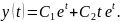
Тогда

Итак,
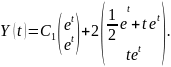
Мы опускаем строгое обоснование метода сведения системы дифференциальных уравнений к одному уравнению.
§2. Системы линейных дифференциальных уравнений.
Система дифференциальных уравнений называется линейной, если уравнения системы линейны относительно всех компонент неизвестной вектор-функции и их производных, т.е. имеют вид:
 (2.1)
(2.1)
Обозначаем
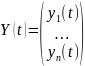 ,
,
 ,
, 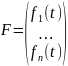 ,
,
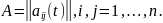
Тогда систему (2.1) можно переписать в виде
 (2.2)
(2.2)
Если
в системе (2.2)
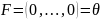 ,
то система (2.2) называется системой
линейных однородных дифференциальных
уравнений.
,
то система (2.2) называется системой
линейных однородных дифференциальных
уравнений.
Приводим без доказательства следующее утверждение.
Теорема (о структуре общего решения системы линейных однородных дифференциальных уравнений).
Пусть дана система линейных однородных дифференциальных уравнений
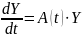 , (2.3)
, (2.3)
где
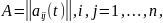 функции
функции
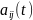 непрерывны на
непрерывны на
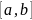 ,
и пусть
,
и пусть
 - линейно независимые на
решения системы (2.3). Тогда общее решение
системы линейных однородных дифференциальных
уравнений (2.3) имеет вид:
- линейно независимые на
решения системы (2.3). Тогда общее решение
системы линейных однородных дифференциальных
уравнений (2.3) имеет вид:

где
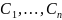 – произвольные постоянные.
– произвольные постоянные.
Любые n линейно неизвестных частных решений системы (2.3) называются её фундаментальной системой решений.
Пусть дана система
 , (2.4)
, (2.4)
где
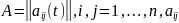 - действительные числа.
- действительные числа.
Так
как постоянные
 непрерывны на любом отрезке
,
то применима сформулированная выше
теорема.
непрерывны на любом отрезке
,
то применима сформулированная выше
теорема.
Частные решения системы (2.4) составляющие фундаментальную систему решений, ищем в виде
 (2.5)
(2.5)
Подставляем (2.5) в уравнение (2.4):
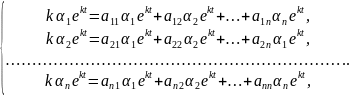
или
 (2.6)
(2.6)
Система
(2.6) – система n
линейных алгебраических однородных
уравнений относительно
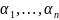 .
Она имеет нетривиальные решения, если
.
Она имеет нетривиальные решения, если
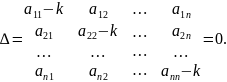
 (2.7)
(2.7)
Уравнение (2.7) называется характеристическим уравнением для системы (2.4), а его корни – характеристическими корнями системы (2.4).
Случай
1. Характеристические
корни уравнения (2.7) действительны и
различны, их ровно n
штук. Пусть это числа
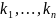 .
Подставляя
.
Подставляя
 в (2.6) находим соответствующие
в (2.6) находим соответствующие
 Фундаментальную систему решений
составляет вектор-функция
Фундаментальную систему решений
составляет вектор-функция
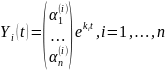 (доказательство линейной независимости
(доказательство линейной независимости
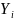 опускаем). Тогда по приведённой теореме
общее решение системы уравнений (2.4)
имеет вид:
опускаем). Тогда по приведённой теореме
общее решение системы уравнений (2.4)
имеет вид:

Пример 2. Решить систему уравнений
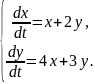 (2.8)
(2.8)
Решение. Записываем соответствующее характеристическое уравнение:
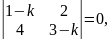
или
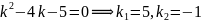
Частные решения ищем в виде
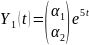 и
и

Подставляем
 в систему (2.8):
в систему (2.8):
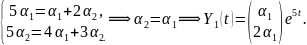
Пусть
 ,
тогда
,
тогда
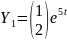 .
.
Аналогично
находим


Пусть
 ,
тогда
,
тогда
 .
.
Итак, общее решение системы (2.8):
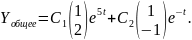
Случай
2. Среди
характеристик корней уравнения (2.7) есть
комплексные. Пусть комплексно-сопряжённые
числа
 и
и
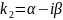 являются корнями характеристического
уравнения (2.7). В этом случае вместо
комплекснозначных вектор-функций
являются корнями характеристического
уравнения (2.7). В этом случае вместо
комплекснозначных вектор-функций
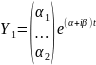 и
и
 в фундаментальную систему решений
включаем функции
в фундаментальную систему решений
включаем функции
 и
и
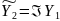 (тот факт, что
(тот факт, что
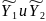 - решения и линейно независимы, принимаем
без доказательства).
- решения и линейно независимы, принимаем
без доказательства).
Тогда по теореме общее решение системы уравнений (2.4) имеет вид:
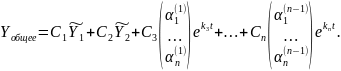
Пример 3. Решить систему уравнений
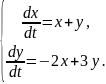 (2.9)
(2.9)
Решение. Записываем соответствующее характеристическое уравнение:

или
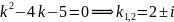 .
.
Частные решения ищем в виде
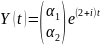
Подставляем в систему (2.8):
 .
.
Пусть
,
тогда
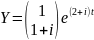 – частное решение (2.9).
– частное решение (2.9).
Значит
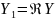 ,
,
 .
Имеем:
.
Имеем:
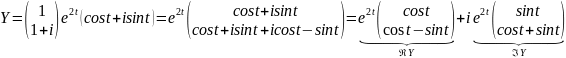
Таким образом, общее решение системы (2.9):
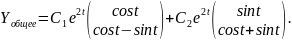
Случай
3.
Среди характеристических корней
уравнения (2.7) есть кратные. Пусть
характеристический корень
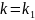 имеет кратность r.
Частные решения, входящие в фундаментальную
систему решений и соответствующие корню
имеет кратность r.
Частные решения, входящие в фундаментальную
систему решений и соответствующие корню
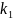 ,
ищем в виде:
,
ищем в виде:

Тогда общее решение системы уравнений (2.4) будет иметь вид:

Пример 4. Решить систему уравнений
 (2.10)
(2.10)
Решение. Записываем соответствующее характеристическое уравнение:
или
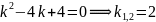 .
.
Решение системы (2.10) ищем в виде:
 (2.11)
(2.11)
Подставляем (2.11) в систему (2.10):
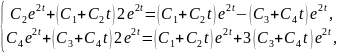
или
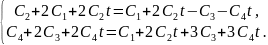
Отсюда

тогда
Итак, общее решение системы (2.10):

Описанный метод нахождения решения системы линейных однородных дифференциальных уравнений (2.4) называется методом собственных векторов.
