
2. Основные законы и формулы по разделам курса физики
2.1. Электростатика
Закон сохранения заряда в замкнутой системе:
![]() .
.
Закон Кулона:
 (в вакууме),
(в вакууме),
 (в среде),
(в среде),
где F – сила взаимодействия двух точечных зарядов q1 и q2; r – расстояние между зарядами; 0 = 8,8510–12 Ф/м – электрическая постоянная; – диэлектрическая проницаемость среды.
Напряженность электростатического поля
 ,
,
где
![]() – сила, действующая на точечный
положительный заряд q0,
помещенный в данную точку поля.
– сила, действующая на точечный
положительный заряд q0,
помещенный в данную точку поля.
Напряженность электростатического поля точечного заряда q на расстоянии r от заряда
 .
.
Поток
вектора напряженности электрического
поля
![]() (сквозь площадку dS),
(сквозь площадку dS),
![]() (сквозь поверхность S),
(сквозь поверхность S),
![]() (сквозь замкнутую поверхность S),
где
(сквозь замкнутую поверхность S),
где
![]() – вектор, модуль
которого равен dS,
а направление совпадает с нормалью
– вектор, модуль
которого равен dS,
а направление совпадает с нормалью
![]() к площадке; Еn
– проекция вектора
к площадке; Еn
– проекция вектора
![]() на нормаль
к площадке dS.
на нормаль
к площадке dS.
Принцип суперпозиции электростатических полей
 ,
,
где
![]() – напряженность поля, создаваемого
зарядом qi.
– напряженность поля, создаваемого
зарядом qi.
Плотность зарядов (линейная, поверхностная, объемная):
![]()
![]()
![]() .
.
Теорема Гаусса для электростатического поля в вакууме:
– в случае дискретного распределения зарядов
 ;
;
– в случае непрерывного распределения зарядов
 ,
,
где
![]() – алгебраическая сумма зарядов,
заключенных внутри замкнутой поверхности
S;
n
– число зарядов;
– объемная плотность зарядов.
– алгебраическая сумма зарядов,
заключенных внутри замкнутой поверхности
S;
n
– число зарядов;
– объемная плотность зарядов.
Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью
 ,
,
где – поверхностная плотность заряда.
Напряженность поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями,
 ,
,
где – поверхностная плотность заряда.
Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом R с общим зарядом q на расстоянии r от центра сферы,
![]() при r
< R
(внутри сферы);
при r
< R
(внутри сферы);
при
![]() (вне сферы).
(вне сферы).
Напряженность поля, создаваемого объемно заряженным шаром радиусом R с общим зарядом q на расстоянии r от центра шара,
 при
при
![]() (внутри шара);
(внутри шара);
при (вне шара).
Напряженность поля, создаваемого равномерно заряженным бесконечным цилиндром радиусом R на расстоянии r от оси цилиндра,
при r < R (внутри цилиндра);
 при
(вне цилиндра),
при
(вне цилиндра),
где – линейная плотность заряда.
Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура
![]() ,
,
где
El
– проекция вектора
на направление элементарного перемещения
![]() .
Интегрирование производится по любому
замкнутому пути L.
.
Интегрирование производится по любому
замкнутому пути L.
Потенциальная энергия заряда q0 в поле заряда q на расстоянии r от него
 .
.
Потенциал электростатического поля
 ,
,
 ,
,
где
q0
–
точечный положительный заряд, помещенный
в данную точку поля;
U
–
потенциальная энергия заряда q0;
![]() – работа перемещения заряда q0
из данной точки поля за его пределы.
– работа перемещения заряда q0
из данной точки поля за его пределы.
Потенциал электростатического поля точечного заряда на расстоянии r от заряда
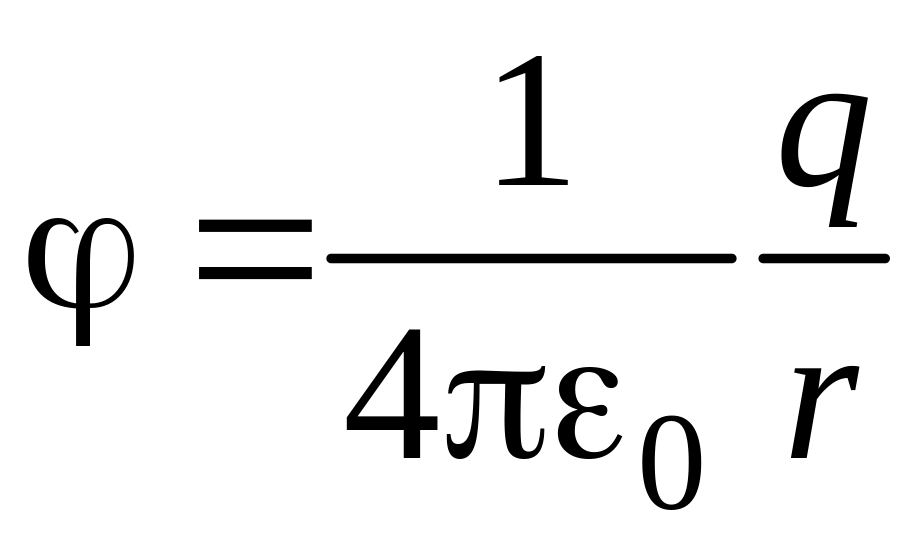 .
.
Связь между напряженностью и потенциалом электростатического поля
![]()
 ,
,
где
![]() – единичные векторы координатных осей.
Знак «минус» определяется тем, что
вектор
поля направлен в сторону убывания
потенциала.
– единичные векторы координатных осей.
Знак «минус» определяется тем, что
вектор
поля направлен в сторону убывания
потенциала.
В случае поля, обладающего центральной или осевой симметрией,
![]() .
.
Работа, совершаемая силами электрического поля при перемещении заряда q0 из точки 1 в точку 2,
![]()
 ,
,
где El – проекция вектора на направление элементарного перемещения .
Разность потенциалов между двумя точками 1 и 2 в электростатическом поле
 ,
,
где A12 – работа, совершаемая силами электростатического поля при перемещении заряда q0 из точки 1 в точку 2; Еl – проекция вектора на направление элементарного перемещения ; интегрирование производится вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.
Разность потенциалов между точками, находящимися на расстоянии х1 и х2 от равномерно заряженной бесконечной плоскости,
 ,
,
где – поверхностная плотность заряда.
Разность потенциалов между бесконечными разноименно заряженными плоскостями, расстояние между которыми равно d,

Разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра равномерно заряженной сферической поверхности (объемно заряженного шара) радиусом R с общим зарядом q, причем r1 > R, r2 > R, r2 >r1,

Разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра объемно заряженного шара радиусом R с общим зарядом q, причем r1 < R, r2 < R, r2 >r1,

Разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от оси равномерно заряженного с линейной плотностью бесконечного цилиндра радиусом R, причем r1 > R, r2 > R, r2 >r1,

Поляризованность диэлектрика
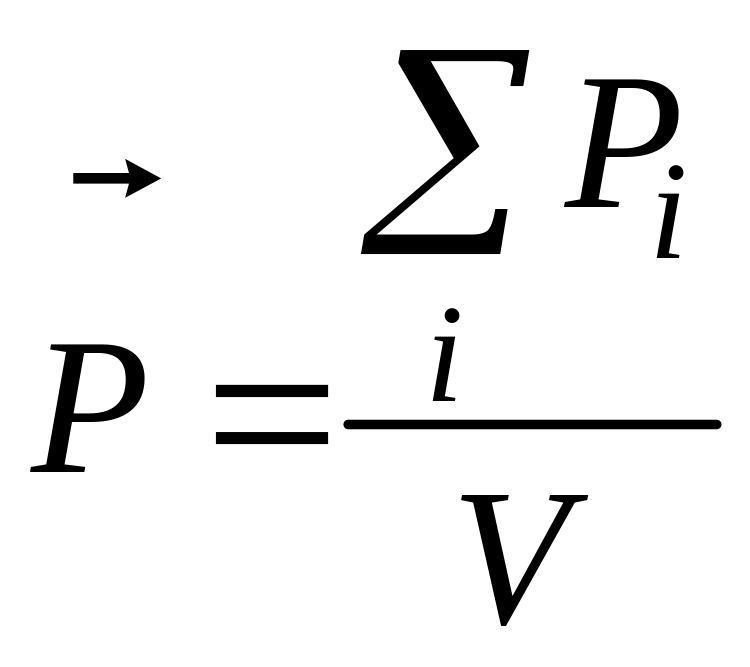 ,
,
где V
– объем диэлектрика;
![]() – дипольный момент i-ой
молекулы.
– дипольный момент i-ой
молекулы.
Связь между поляризованностью диэлектрика и напряженностью электростатического поля:
![]() ,
,
где – диэлектрическая восприимчивость вещества; 0 –электрическая постоянная.
Связь диэлектрической проницаемости с диэлектрической восприимчивостью :
![]()
Связь между напряженностью Е поля в диэлектрике и напряженностью Е0 внешнего поля:

![]() ,
,
где P – поляризованность, – диэлектрическая проницаемость.
Связь
между векторами электрического смещения
![]() ,
напряженности электростатического
поля
и поляризованности
,
напряженности электростатического
поля
и поляризованности
![]() :
:
![]()
![]()
Теорема Гаусса для электростатического поля в диэлектрике:
 ,
,
где
– алгебраическая сумма заключенных
внутри замкнутой поверхности S
свободных
электрических зарядов; Dn
– проекция вектора
на нормаль
к площадке
![]() ,
– вектор, модуль которого равен dS,
а направление совпадает с нормалью
к площадке.
,
– вектор, модуль которого равен dS,
а направление совпадает с нормалью
к площадке.
Условия на границе раздела диэлектрических сред (проницаемость которых 1 и 2) при отсутствии на границе свободных зарядов:
![]()
![]()

 ,
,
где
![]() ,
D
и
En,
Dn
– тангенциальные и нормальные составляющие
векторов
и
соответственно.
,
D
и
En,
Dn
– тангенциальные и нормальные составляющие
векторов
и
соответственно.
Напряженность электростатического поля у поверхности проводника
 ,
,
где – поверхностная плотность зарядов, – диэлектрическая проницаемость среды, окружающей проводник.
Электроемкость уединенного проводника
![]() ,
,
где q – заряд, сообщенный проводнику; – потенциал проводника.
Электроемкость шара радиусом R
![]()
Электроемкость конденсатора
 ,
,
где q – заряд, накопленный в конденсаторе; (1 – 2) – разность потенциалов между его пластинами.
Электроемкость плоского конденсатора
![]() ,
,
где S – площадь каждой пластины конденсатора; d – расстояние между пластинами.
Электроемкость сферического конденсатора
 ,
,
где r1 и r2 – радиусы концентрических сфер.
Электроемкость цилиндрического конденсатора
 ,
,
где l – длина пластин конденсатора; r1 и r2 – радиусы полых коаксиальных цилиндров.
Энергия уединенного заряженного проводника
 ,
,
где C, q, – электроемкость, заряд и потенциал проводника соответственно.
Энергия заряженного конденсатора
 ,
,
где q – заряд конденсатора, С – его электроемкость, – разность потенциалов между пластинами.
Сила притяжения между двумя разноименно заряженными обкладками конденсатора
 ,
,
где q – заряд конденсатора; – поверхностная плотность заряда; S – площадь пластины конденсатора; Е – напряженность электростатического поля; 0 – электрическая постоянная; – диэлектрическая проницаемость.
Энергия электростатического поля плоского конденсатора
 ,
,
где S – площадь сечения одной пластины; U – разность потенциалов между пластинами; V = Sd – объем конденсатора.
Объемная плотность энергии электростатического поля
 ,
,
где E – напряженность электростатического поля; D – электрическое смещение.
