Завдання 8

Підібрати переріз балки (схеми рис. 6.17) в формі прямокутника з відношенням висоти до основи матеріал балок – сталь. [σ]=160 МПа.

Дані для розрахунку взяти з табл. 6.2.

Таблиця 6.2

Схема	F, кН	М, кНм	g, кН/м	а	b	c
				M
0	20	10	10	1	2	1
І	30	20	15	2	4	2
ІІ	15	30	10	3	3	2
ІІІ	10	40	20	2	2	1
ІV	20	30	15	3	4	1
V	30	20	10	1	2	2
VI	15	10	20	4	3	1
VII	10	40	25	2	1	2
VIII	25	30	10	3	3	1
IX	20	20	20	2	1	2

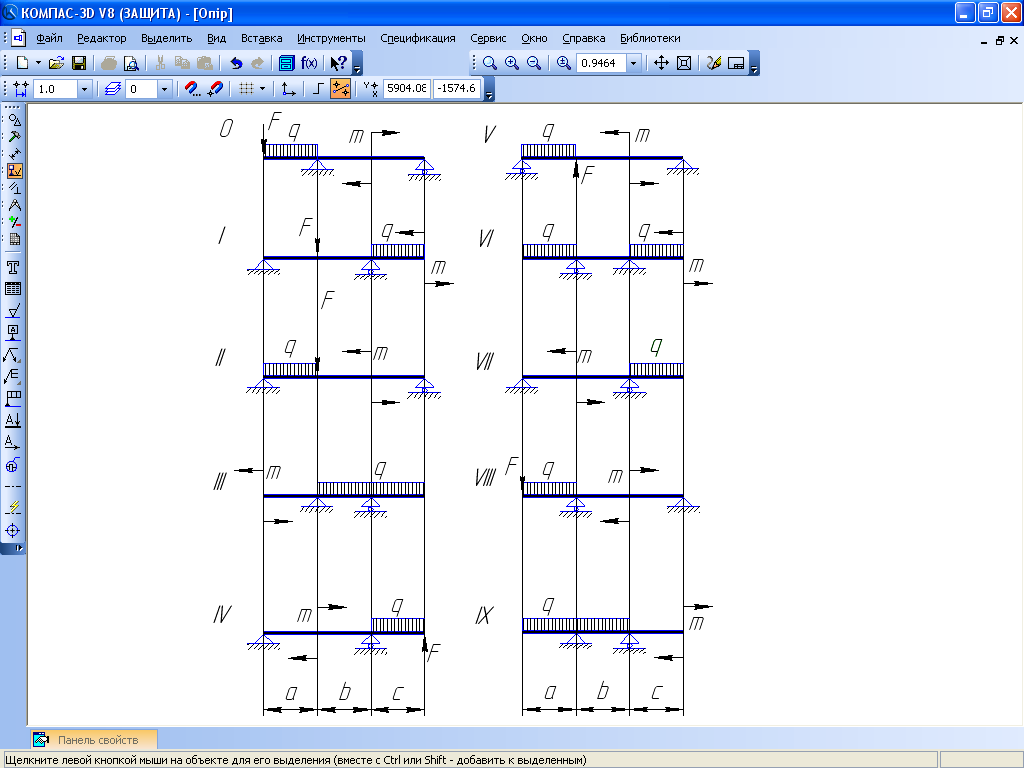
Рис. 6.17

Приклад розв’язання (схема приведена на рис.6.18).

Якщо в попередньому, 7-му завданні проводиться перевірочний розрахунок балки, то тут необхідно підібрати розміри перерізу, тобто провести проектний розрахунок.

Вихідним для розрахунку є умова міцності при згині: (6.3).

Очевидно, що розміри слід підбирати в небезпечному перерізі балки – в тому, де діє найбільший момент. Якщо ці розміри будуть забезпечувати міцність в найбільш небезпечному перерізі, то і в інших перерізах міцність буде забезпечена.

З виразу (6.3) бачимо, що:

(6.4)

Для прямокутника:

Враховуючи, що за умовою отримаємо:

Після підстановки в (6.4):

(6.5)

В (6.5) М являє собою момент в небезпечному перерізі, тобто найбільший, максимальний.

Для визначення ж небезпечного перерізу і максимального моменту необхідно побудувати епюру згинаючих моментів. Для контролю правильності побудови епюри М будемо будувати також епюру Q.

Якщо провести довільний переріз І-І (див. рис.6.18а) і для визначення внутрішніх силових факторів в перерізі розглядати рівновагу відрізаної частини (метод перерізів), то і зліва, і з права від перерізу є опори балки; реакціями опор є сили, які прикладені до балки – ці реакції невідомі. Для розрахунку балки їх необхідно визначити.

Отже, при побудові епюр роботу необхідно розпочинати з визначення реакцій опор балки. Це можна зробити, складаючи рівняння рівноваги для балки як тіла, що знаходиться в рівновазі під дією зовнішніх зусиль і реакцій.

Згадаємо, що для плоскої врівноваженої системи сил повинні виконуватись три незалежних рівняння рівноваги. З іншого боку, в нашому випадку ліва, шарнірно-нерухома опора, може мати дві реакції і (див. рис. 6.3), а права, шарнірно-нерухома – одну реакцію . Отже, отримаємо систему трьох рівнянь з трьома невідомими реакціями, які можна визначити з цієї системи.

Рівняння рівноваги балки:

Рівномірно розподілене по довжині навантаження q можна уявити собі як, наприклад, шар цегли постійної висоти, який викладено вздовж дошки, чи власну вагу балки. Нагадаємо, що інтенсивність такого навантаження q, є величина навантаження, що приходиться на один погонний метр. Отже, якщо рівномірно розподілене навантаження інтенсивністю q діє, наприклад, на довжині два метри, то рівнодіюча цього навантаження буде дорівнювати 2q і прикладена посередині цієї довжини.

При складанні рівнянь рівноваги розподілене навантаження можна замінити його рівнодіючою. На рис.6.18а момент від розподіленого навантаження відносно точки А дорівнює , де – рівнодіюча, а 1м – плече цієї рівнодіючої відносно точки А.

Крім того, при складанні перших двох рівнянь (суми проекцій) слід пам’ятати, що проекція моменту на будь-яку вісь дорівнює нулю.

З останнього рівняння:

з другого:

Визначення реакцій складає невелику частину роботи по побудові епюр. Однак, якщо реакції будуть визначені неправильно, епюра також буде неправильною і розрахунки потрібно буде повторити. Щоб цьому запобігти, необхідно перевірити правильність визначення реакцій опор.

Якщо система знаходиться в рівновазі, сума моментів всіх сил (і реакцій) відносно будь-якої точки повинна рівнятися нулю.

Тому для перевірки складемо суму моментів відносно точки опори В. Якщо реакція визначена правильно, ця сума буде дорівнювати нулю.

Отже, реакції визначено правильно.

Переходимо до побудови епюр Q і М. Правила побудови епюр і правило знаків розглянуті в прикладі до завдання № 7.

Для студента, який виконав це завдання, видно, що балка яку розглядаємо, має три ділянки. Для кожної з яких використані свої рівняння рівноваги силових факторів.

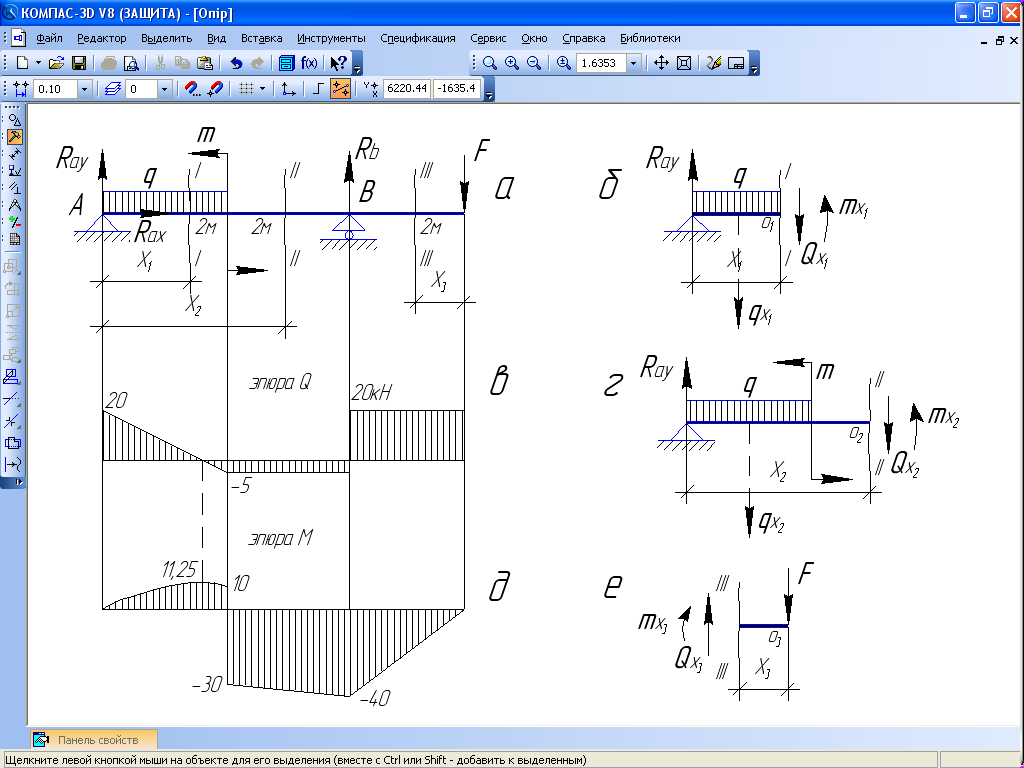
Рис. 6.18

Розріжемо балку перерізом І-І і розглянемо рівновагу відрізаної лівої частини (див.мал.6.18б).

Ця частина балки знаходиться в рівновазі під дією прикладених до неї реакції R_Ay, частини розподіленого навантаження q, невідомих внутрішніх силових факторів в перерізі Qх₁ і Мх₁, які ми приймаємо як додатні (див. приклад до завдання 7).

Переріз 1-1 визначається текучою координатою х₁, яка змінюється в межах 0≤х₁≤2 м.

Рівняння рівноваги відрізаної частини:

Звідси:

При складанні рівнянь рівноваги дія розподіленого навантаження враховувалась так, як і при визначенні реакцій опор. Оскільки частина балки, що розглядається, має довжину х₁ (м), то рівнодіюча, прикладеної до цієї частини рівномірно розподіленого навантаження буде дорівнювати qx₁ і прикладена посередині довжини х₁, тобто на відстані від точки О₁. На рис.6.18б рівнодіюча рівномірно розподіленого навантаження, що дорівнює qx₁, зображена пунктирним вектором.

З отриманих виразів Qх₁ і Мх₁ виходить, що Qх₁ є лінійна функція х₁, а Мх₁ – квадратна. Епюра Qх₁ буде зображена прямою лінією, а епюра Мх₁ – параболою. Для побудови епюри Qх₁ достатньо двох точок, а для епюри Мх₁ їх необхідно мінімум три.

Будуємо епюру Qх₁ на першій ділянці 0≤х₁≤2.

При

При

З’єднуючи отримані точки (0;15) і (2;-5) прямою, отримуємо епюру Q на першій ділянці (див.рис.6.18в).

Будуємо епюру М₁.

З’єднуючи отримані точки з координатами (0;0), (1;10), (2;10), отримаємо параболу, яка на даній ділянці має екстремум (максимум). Для точного визначення екстремального моменту Мх₁е і перерізу в якому він діє, використаємо диференціальну залежність між Q та М: , тобто Q – перша похідна від моменту по довжині балки. Відомо, що при значенні аргументу х₁₀, яке зводить першу похідну (Q) в нуль, первісна функція (М) має екстремальне значення.

Визначаємо значення х₁₀ з умови:

Отже, екстремальний момент діє в перерізі на відстані 1,5м від лівої опори. Підставляючи це значення х₁₀ в рівняння моменту, отримаємо екстремальне значення Мх₁е.

Таким чином отримаємо четверту точку параболи з координатами (1,5, 11,25). З’єднуючи ці точки, отримаємо епюру М на першій ділянці (див.рис.6.18д).

Друга ділянка. Відрізана перерізом ІІ-ІІ ліва частина балки показана на рис.6.18г. Довільний переріз ІІ-ІІ визначається текучою координатою х₂, відлік якої беремо від лівої опори. Межі х₂: 2≤х₂≤4

Рівняння рівноваги для лівої частини:

Звідси:

Тут Qх₂ – постійна величина, її епюра на цій ділянці пряма, паралельна вісі епюри (див.рис.6.18в).

Мх₂ – лінійна функція х₂. Пряму епюри, яка представляє цю функцію, будуємо по двом точкам:

Третя ділянка. Розріжемо балку перерізом ІІІ-ІІІ на ділянці, що залишилась. Для визначення внутрішніх силових факторів в цьому перерізі можна розглянути рівновагу як лівої, так і правої частини балки.

Очевидно, доцільніше розглянути рівновагу правої частини, так як до неї прикладена всього одна зовнішня сила F (рис. 6.18а), і тому рівняння рівноваги будуть значно спрощені, ніж при розгляданні лівої частини. Внутрішні силові фактори в перерізі доцільно прикласти так, якби вони були додатні (див. мал. 6.18а), тобто, щоб праву частину від перерізу поперечна сила Qх₃ зсувала вверх, а момент Мх₃ згинав відрізану частину балки випуклістю вниз.

Для текучої координати х₃, яка визначає довільний переріз ІІІ-ІІІ, будемо брати відлік від кінця консолі, де прикладена сила F (див. рис. 6.18а). Вісь х₃ направляємо при цьому вліво, тоді х₃ змінюється в межах 0≤х₃≤2.

Рівняння рівноваги для даної частини балки:

Звідси:

Як і на другій ділянці, Qх₃ – величина постійна, а Мх₃ – лінійна функція від х₃, графічне зображення якої на епюрі будуємо по двом точкам.

Від’ємний знак моменту означає, що ми невірно вибрали напрямок Мх₃ на рис. 6.18е. Для рівноваги цей момент повинен діяти в іншу сторону, проти стрілки годинника, що в даному випадку очевидно. Якщо ж змінити напрямок моменту Мх₃, то з рівняння рівноваги він вийде додатнім,але буде згинати відрізану частину випуклістю вверх, тобто за прийнятим правилом знаків для епюр знову буде від’ємним.

Оскільки спочатку невідомий момент Мх₃ був направлений як додатній за правилом знаків для епюр, його знак, що ми отримали з рівняння рівноваги, співпав зі знаком, прийнятим для моменту при побудові епюр.

По точкам (0;0) і (2;-40) будуємо епюру Мх₃ на третій ділянці (див. рис. 6.18д).

По побудованій епюрі М встановлюємо, що максимальне значення моменту дорівнює 40 кНм.

Підставляючи це значення у вираз 6.5 , отримаємо:

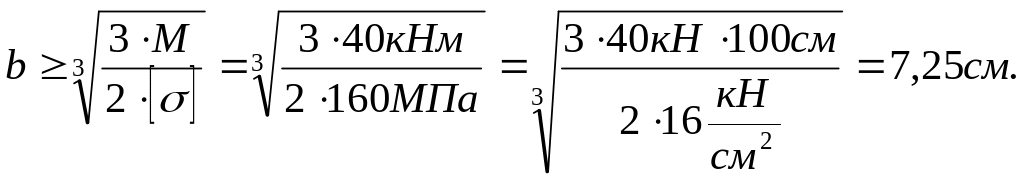
Отже, раціональним перерізом балки є прямокутник з розмірами і

При такому перерізі нормальні напруження в найбільш небезпечних перерізах будуть дорівнювати допустимим, а у всіх інших перерізах – менше допустимих.

Найбільш небезпечний переріз там де діє максимальний момент, на найбільшій відстані від нейтральної вісі перерізу.