Завдання 3

Визначити діаметр поперечного перерізу стержнів системи. Матеріал стержнів сталь, [σ]=160 МПа. Схеми вказані на рис. 1.11, дані взяти з табл. 1.3.

Таблиця 1.3

Схема	а,м	в,м	F,град	α,град
0	2	4	40	30
І	1	2	20	60
ІІ	3	5	50	45
ІІІ	4	2	40	30
ІV	5	10	100	45
V	2	6	40	30
VI	3	6	60	60
VII	4	5	70	45
VIII	2	4	100	60
IX	1	2	50	30

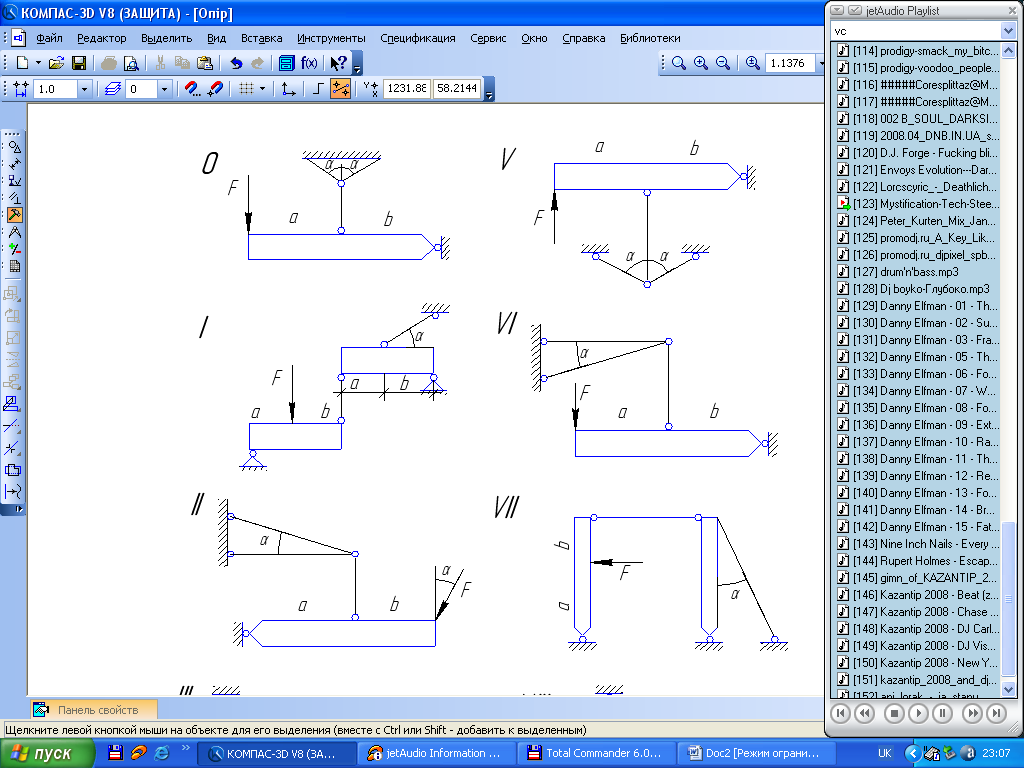
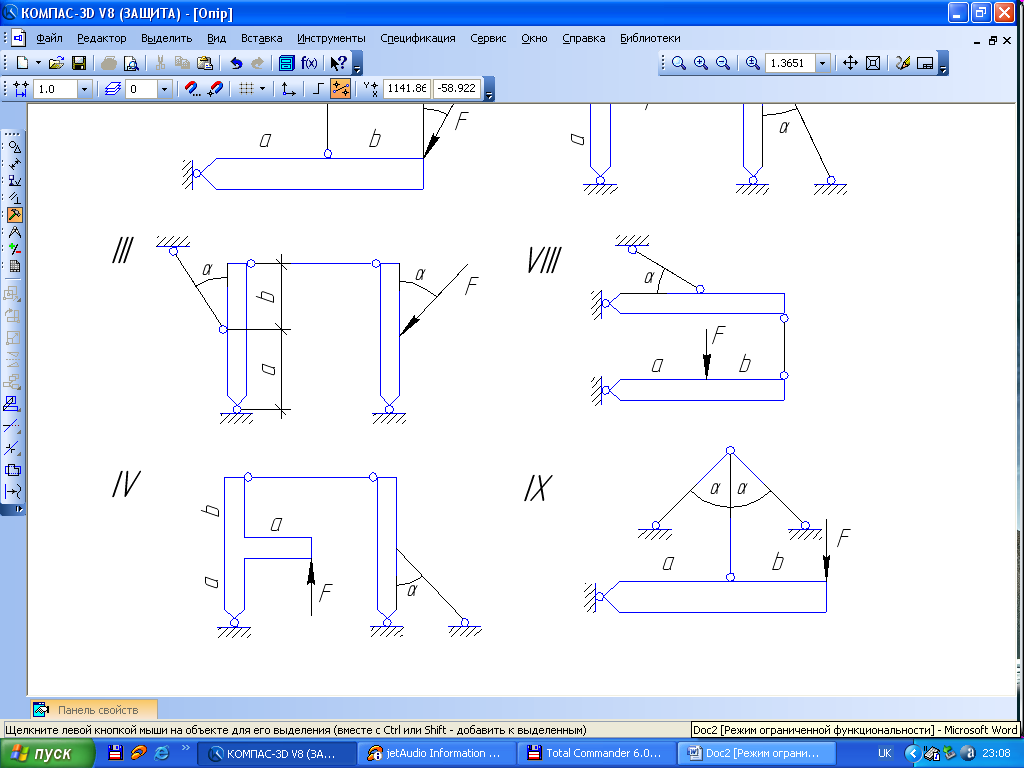
Рис. 1.11

Приклад: (див. схему на рис. 1.12): F=15кН; а=4м; в=1м; α=30º.

Це задача ІІ типу, приклад проектного розрахунку. Для її вирішення використовуємо умову міцності при розтягу:

Звідки:

Для круглого перерізу :

.

(1.3)

Отже, для вирішення задачі потрібно спочатку знайти повздовжні зусилля в стержнях АВ і СД, потім з формули (1.3) – діаметри цих стержнів.

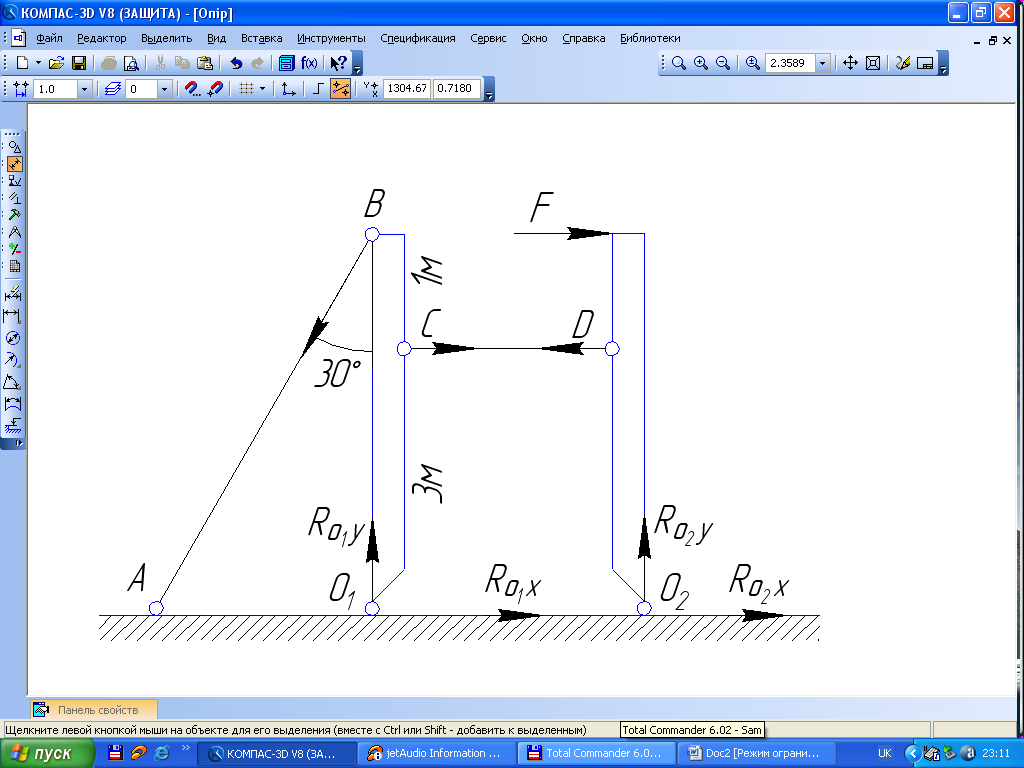
Рис. 1.12

Ця задача також, як і попередня, – статично визначена. Насправді, виділимо з системи правий брус і покажемо зусилля, під дією яких він знаходиться в рівновазі(мал. 1.13,а).

Як видно з рисунка, на брус діють 3 невідомі реакції, які можуть бути визначені з 3 рівнянь рівноваги для плоскої врівноваженої системи сил. Як і в попередньому прикладі, для знаходження реакції стержня СД достатньо прирівняти до нуля суму моментів сил, які діють на брус, який розглядаємо, відносно т.О₂:

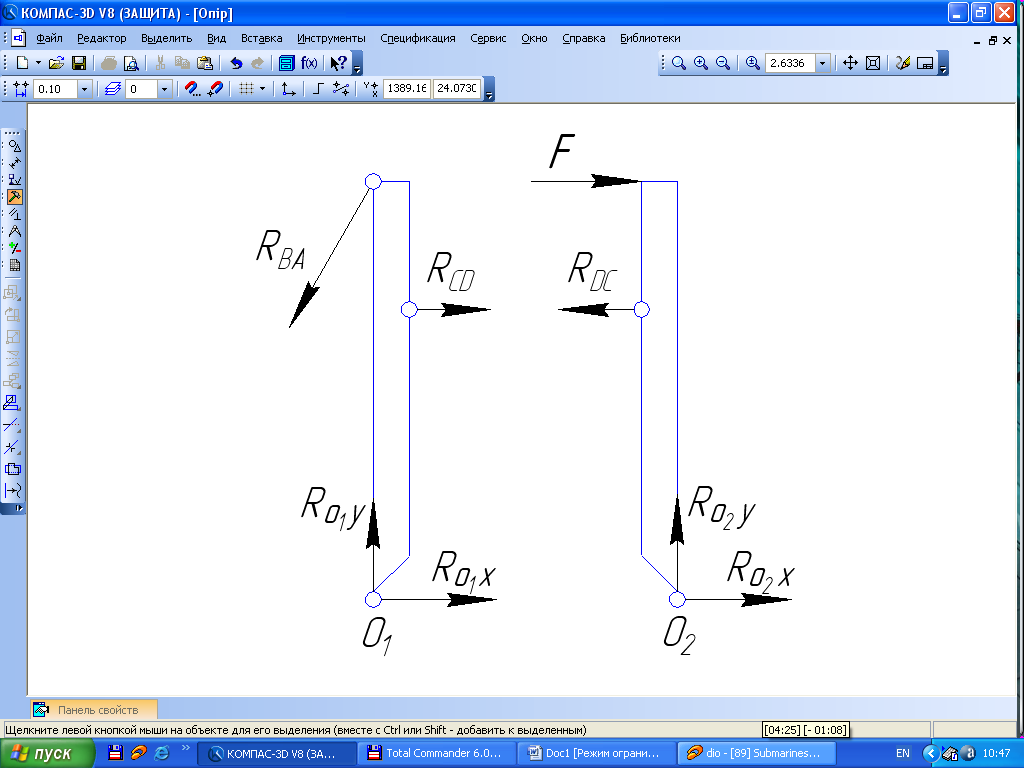
а б

Рис. 1.13

;

Оскільки отримане з рівняння рівноваги значення реакції додатне, сила дії стержня СД на брус (реакція стержня) правильно представлена вектором . А, якщо так, то стержень І розтягнутий: намагаючись стиснутись, він тягне правий шарнір вліво (а лівий – вправо), і діюче повздовжнє зусилля в ньому (див. рис. 1.12).

Тепер розглянемо рівновагу лівого бруса. До нього також прикладені три невідомі реакції , так як реакція уже відома.

Оскільки стержень СD розтягнутий, він, намагаючись стиснутись, тягне лівий брус вправо (рис. 1.13,б). Після того як реакція даного стержня визначена, прикладати її до бруса слід тільки в тому напрямку, в якому вона в дійсності діє на брус. Інакше можна неправильно визначити зусилля в останніх стержнях системи.

Складаючи суму моментів сил, діючих на лівий брус і прирівнюючи її до нуля, отримаємо значення повздовжнього зусилля в стержні АВ.

На сам кінець визначимо діаметри поперечних перерізів стержнів І і ІІ. З формули (1.3):

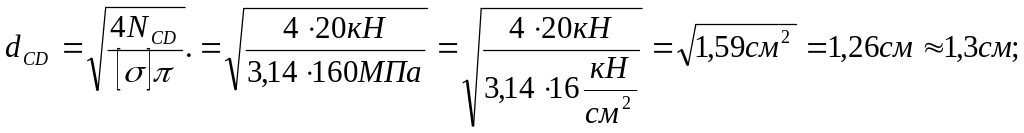
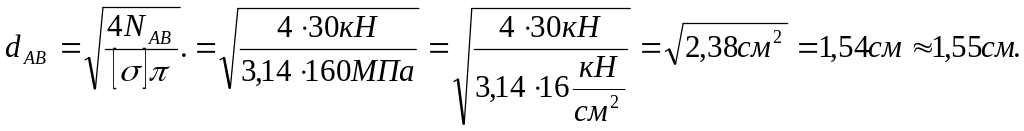
Завдання 4

Визначити зусилля в стержнях системи. Схеми показані на рис. 1.14, дані взяти з табл.1.4. матеріал стержнів – сталь.

Таблиця 1.4

Схема	а,м	в,м	с,м	α,град	F,кН	А1/А2
0	1	1	1	30	20	2
I	2	1	2	45	30	1
II	4	2	1	60	40	2
III	3	1	2	30	20	3
IV	2	4	1	30	10	2
V	4	1	2	60	20	2
VII	1	1	2	30	50	3
VII	5	3	2	45	30	1
VIII	3	2	2	60	20	2
IX	2	2	2	30	50	2

Примітка – площі поперечного перерізу відповідно першого і другого стержнів.

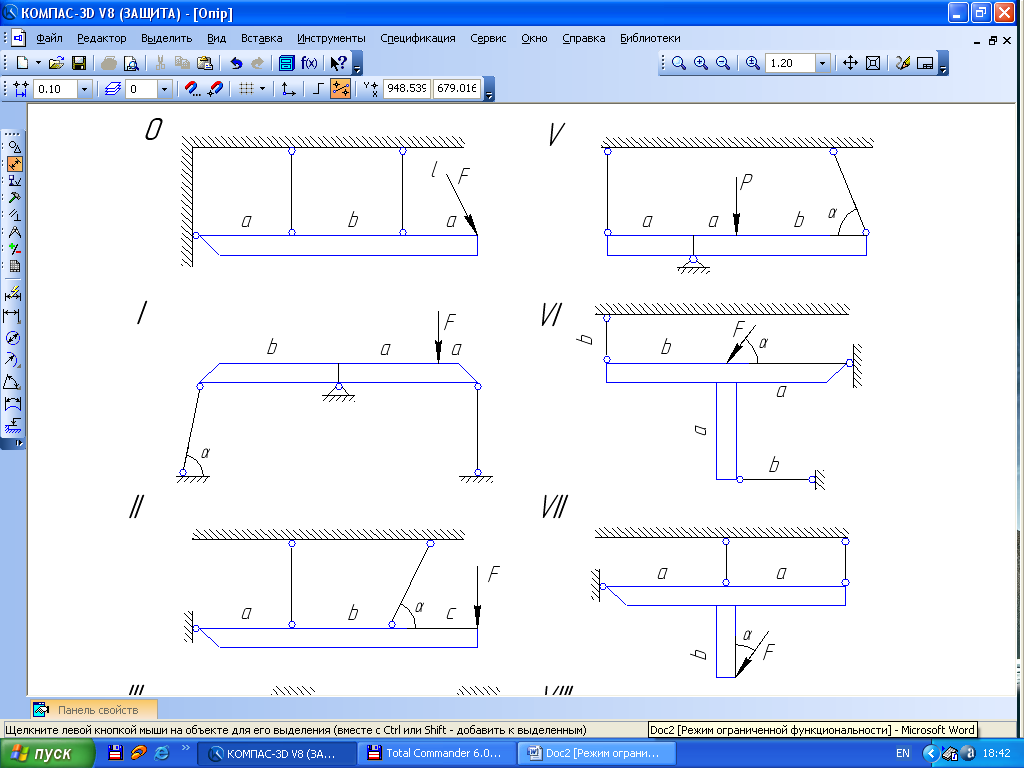
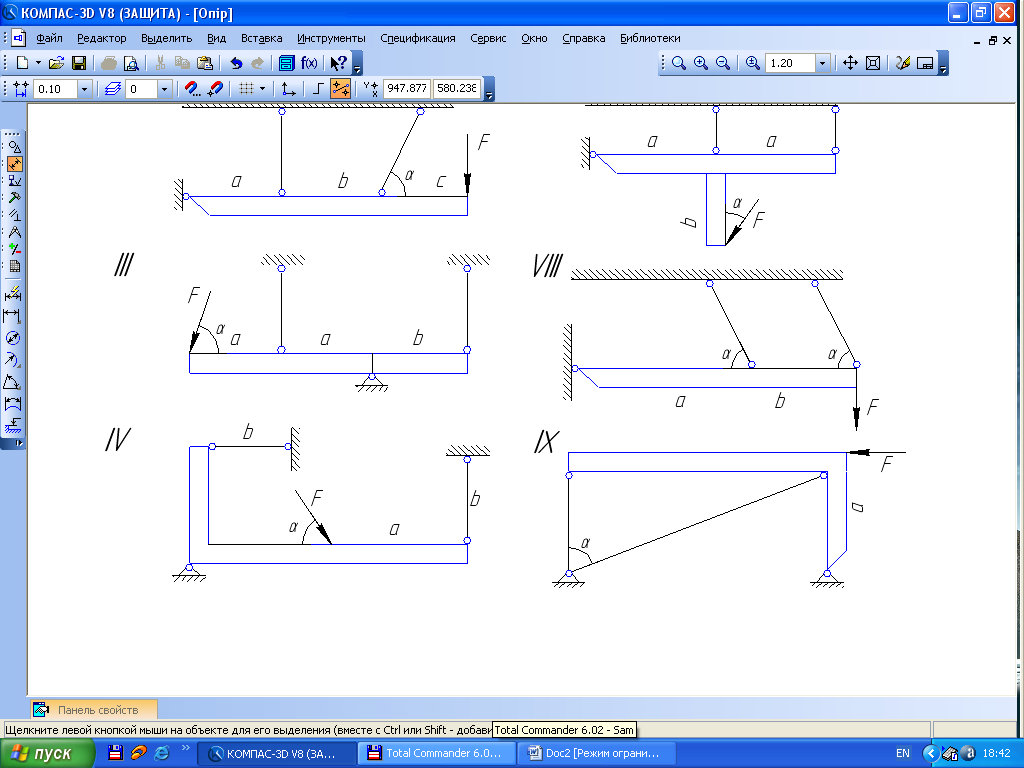
Рис. 1.14

Приклад розв’язання (див. схему на рис. 1.15): а=1м; в=2м; с=1м; А₁/А₂ = 2; F=20кН.

Всім величинам, зв’язаним з лівим стержнем АВ, надається індекс 1, з правим СD – індекс 2.

Відкинемо зв’язки і замінимо їх дію на брус реакціями (рис. 1.15,б).

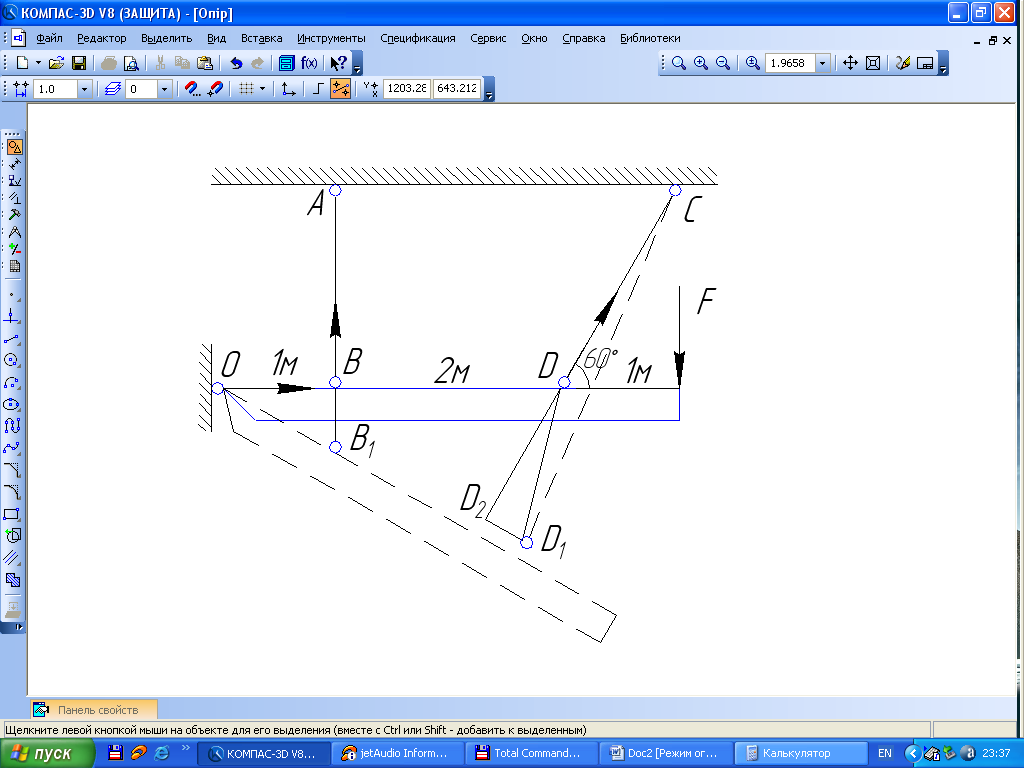а

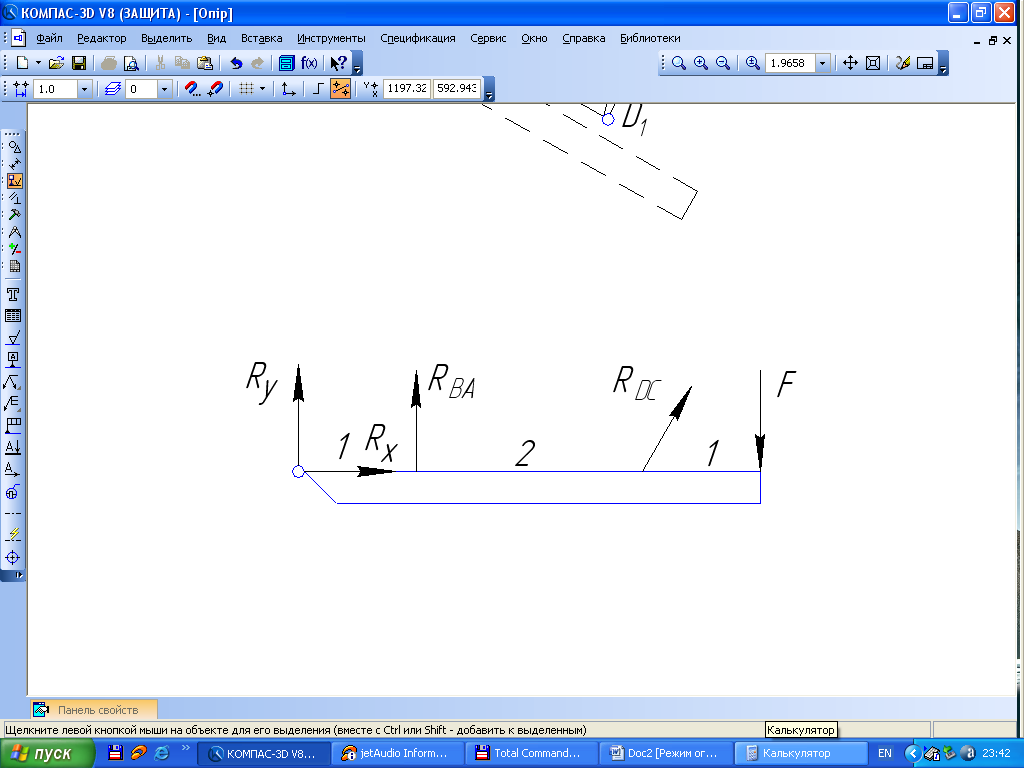б

Рис 1.15

Брус знаходиться в рівновазі під дією 5 зусиль відомої сили F і 4 невідомих реакцій:

Для плоскої зрівноваженої системи сил можна скласти тільки 3 незалежних рівняння рівноваги. Отже, задача – статично невизначена (1 раз).

Для розв’язання потрібно скласти 3 рівняння рівноваги і додати до них ще одне рівняння, яке зв’язує невідомі реакції, яке можна отримати при розгляді умови сумісності деформації системи (рівняння сумісності деформацій).

Вважаючи брус в силу його більшої шорсткості недеформованим, розглянемо положення системи після прикладання сили , яке на рис. 1.15,а показано пунктиром. Оскільки згином бруса нехтуємо, він як абсолютно тверде тіло повернеться навколо т.О. Це повернення бруса обумовлено деформаціями стержнів. Абсолютне видовження стержня АВ: абсолютне видовження стержня СD: .

Нове положення стержня СD можна отримати так: подумки розріжемо шарнір D,подовжимо стержень СD на величину його дійсного видовження і потім, обертаючи навколо т.С приведемо до шарніра В в новому положенні В₁. При цьому повороті внаслідок малості кута повороту, переміщення т.В можна вважати відбувається по дотичній, тобто перпендикулярно радіусу повернення СD₂.

З цієї ж причини переміщення т.В і D також вважаємо, що відбувається по вертикалі, нехтуючи з огляду їх малості горизонтальним зміщенням. Отже, на рис. 1.15,а трикутники ОВВ₁, ОDD₁, DD₂D₁, вважаємо прямокутними. В ∆ DD₂D₁, кут, DD₁D₂ дорівнює α=60º, як кути із взаємно перпендикулярними сторонами.

Тепер з геометричних міркувань отримаємо умову сумісності деформацій, зв’язуючи абсолютні видовження стержнів АВ і СD. Спочатку з прямокутного трикутника DD₂D₁, отримаємо:

(1.4)

Потім з подібності трикутників ОВВ₁ і ОDD₁:

Підставимо сюди вираз DD₁ з (1.4):

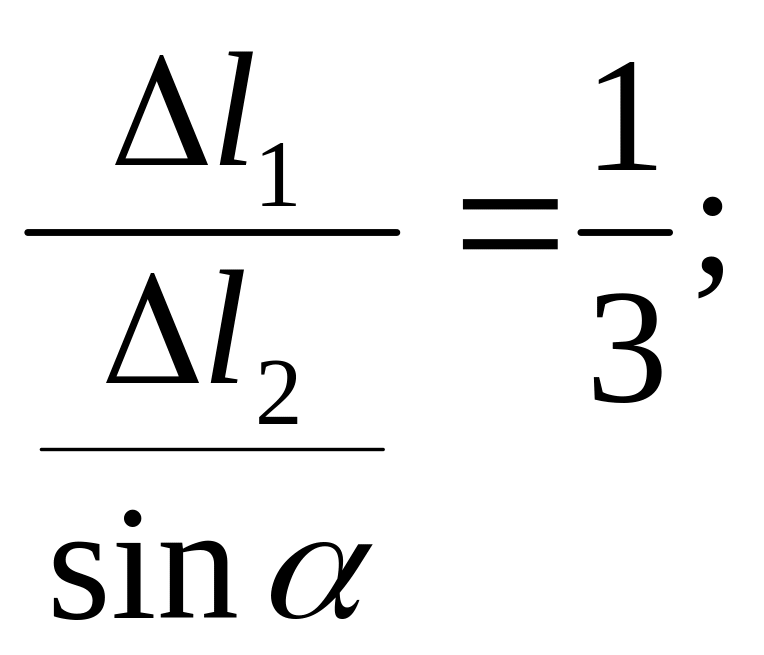
(1.5)

Це і є умова сумісності деформацій стержнів. За законом Гука:

(1.6)

Підставляючи (1.6) в (1.5) отримуємо рівняння сумісності деформацій, яке зв’язує між собою невідомі зусилля і в стержнях.

Оскільки ці зусилля рівні відповідно реакціям і :

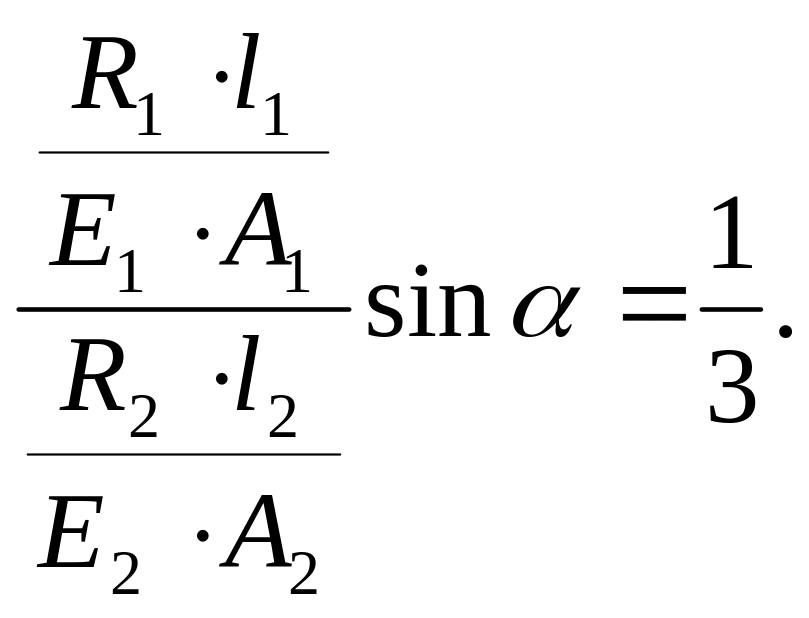(1.7)

Врахуємо, що в даному прикладі

Крім того

Підставляючи цей вираз в (1.7) отримаємо кінцевий вигляд рівняння сумісності деформацій

Це рівняння разом з трьома рівняннями рівноваги складе систему 4 рівнянь з 4 невідомими зусиллями, прикладеними до бруса:

Для визначення зусиль в стержнях достатньо розглянути сумісно лише 3-е і 4-е рівняння. Підставляючи значення з 4-го рівняння в 3-е, отримуємо:

Обидві реакції додатні, напрямлені від вузла, отже, обидва стержні розтягнуті.