
- •Оглавление
- •Введение
- •1. Аналитическая геометрия и линейная алгебра.
- •Занятие № 5. Линейные пространства.
- •Занятие № 6. Евклидовы пространства.
- •Занятие № 7. Линейные операторы и матрицы.
- •Занятие № 10. Скалярное произведение векторов.
- •Занятие № 11. Векторное и смешанное произведение векторов.
- •Занятие № 12. Прямая на плоскости.
- •Занятие № 13. Кривые второго порядка.
- •Занятие № 14. Преобразование координат на плоскости. Приведение уравнений к каноническому виду.
- •Занятие № 15. Плоскость в пространстве.
- •Занятие № 16. Прямая в пространстве.
- •Занятие № 17. Взаимное расположение прямых и плоскостей в пространстве.
- •Занятие № 18. Поверхности в пространстве.
- •2. Введение в математический анализ.
- •21.3. Доказать, что последовательность
- •4. Интегральное исчисление функций одной переменной.
- •5. Дифференциальное исчисление функций нескольких переменных.
- •Занятие № 46. Пределы и непрерывность функции нескольких переменных.
- •Занятие № 47. Частные производные и дифференциалы.
- •Занятие № 48. Касательная плоскость и нормаль к поверхности.
- •Занятие № 49. Производная по направлению. Градиент.
- •6. Интегральное исчисление функций нескольких переменных. Занятие № 53. Двойные интегралы.
- •Занятие № 55. Приложения двойного интеграла.
- •7. Ряды.
- •8. Обыкновенные дифференциальные уравнения.
- •19.1. A) ; б) ; в) ; г) . 19.2. А) ; б) ; в) ; г) . 19.3. А) четная; б) общего вида; в) нечетная.
- •27.4. Касательная , нормаль . 27.5.
- •Рекомендуемая литература
21.3. Доказать, что последовательность
![]()
![]()
![]()
![]()
имеет предел, равный 0.
21.4.
Доказать, что последовательность
![]() сходится к
сходится к
![]() .
.
21.5.
Доказать, что последовательность
![]() не имеет предела при
не имеет предела при
![]() .
.
21.6.
Доказать, что
![]() .
.
21.7.
Доказать, что
![]() .
.
21.8. Имеет ли предел последовательность?
а)
![]() ; б)
; б)
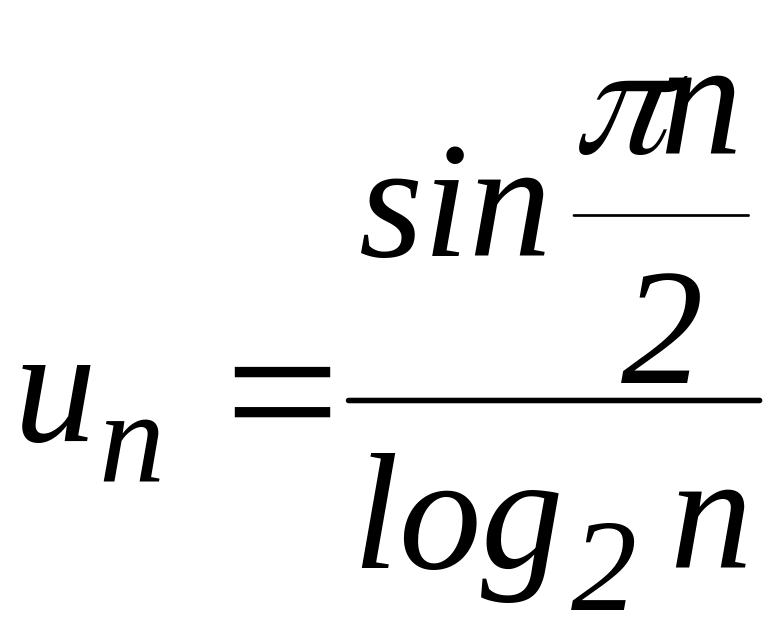 .
.
21.9.
Последовательность
![]() имеет предел
имеет предел
![]() .
.
Доказать,
что
![]() .
.
Что
можно сказать об этом пределе, если
![]() ?
(Привести примеры).
?
(Привести примеры).
21.10. Найти пределы:
а)
![]() ;
б)
;
б)
![]() .
.
21.11. Найти пределы:
а)
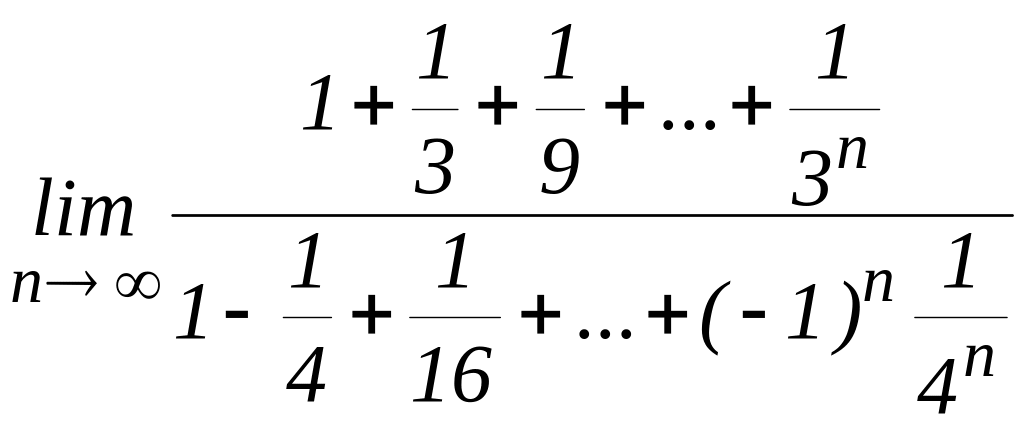 ;
б)
;
б)
![]() .
.
21.12.
Доказать, что последовательность
![]() расходится.
расходится.
21.13.
Доказать, что
![]() .
.
21.13.
Найти
![]() .
.
21.14.
Доказать, что при
![]() справедливо
равенство
справедливо
равенство
![]() .
.
21.15.
Доказать, что
![]() .
.
21.16.
Доказать, что при
справедливо
равенство
![]() .
.
21.17. Доказать, что при справедливо равенство
Занятие № 22.
Вычисление пределов функций с помощью определения и свойств пределов.
22.1.
Доказать, что
![]() .
.
22.2
Доказать, что
![]() .
.
22.3. Найти пределы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
22.4. Найти пределы:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
22.5. Найти пределы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
22.6. Найти пределы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Занятие № 23.
Вычисление пределов функций с помощью алгебраических преобразований.
23.1. Найти пределы рациональных функций:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() .
.
23.2. Найти пределы иррациональных дробей:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ,
,
23.3. Найти пределы в бесконечно удаленных точках:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() ;
з)
;
з)
![]() .
.
Занятие № 24.
Замечательные пределы. Бесконечно малые и бесконечно большие функции.
24.1. С применением первого замечательного предела, вычислить:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
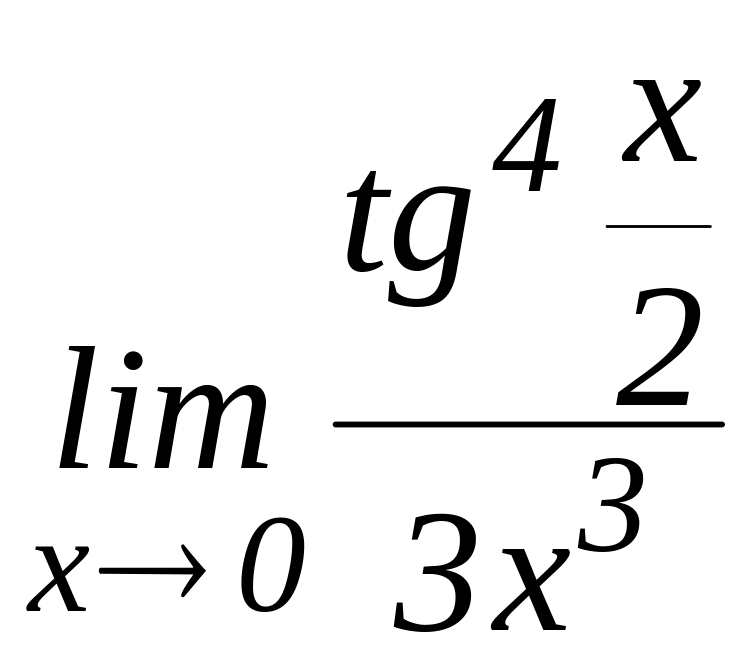 ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
;
и)
![]() ;
к)
;
к)
![]() ;
л)
;
л)
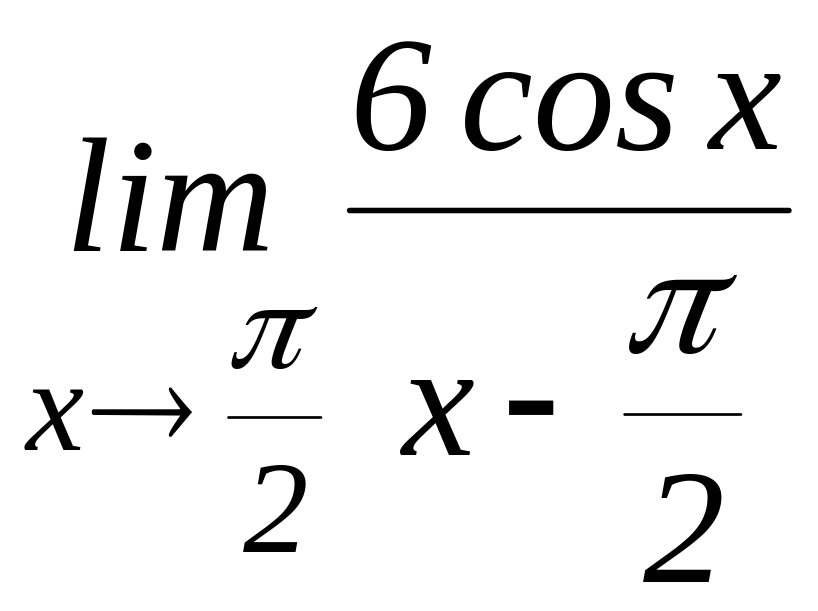 ;
м)
;
м)
![]() .
.
24.2. С применением второго замечательного предела вычислить:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() .
.
24.3. С применением третьего замечательно предела, вычислить:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Занятие № 25.
Вычисление пределов с помощью эквивалентных функций.
Найти пределы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
;
з)
![]() ;
и)
;
и)
![]() ;
к)
;
к)
![]() ;
;
л)
![]() ;
м)
;
м)
![]() .
.
Занятие № 26.
Непрерывность функций и точки разрыва.
26.1.
Исследовать на непрерывность функцию
![]() .
В случае разрыва указать его характер.
.
В случае разрыва указать его характер.
26.2.
Исследовать на непрерывность функцию
![]() .
В случае разрыва указать его характер.
.
В случае разрыва указать его характер.
26.3.
Исследовать на непрерывность функцию
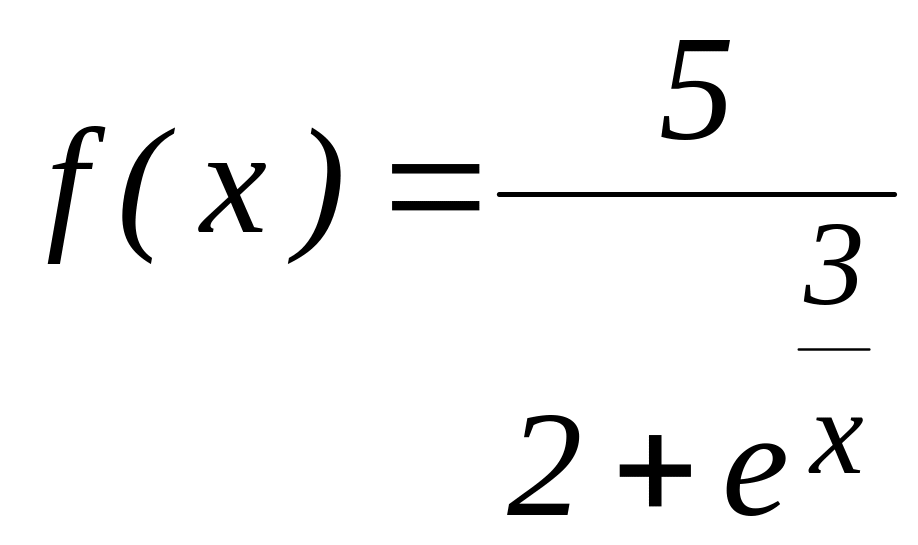 .
В случае разрыва указать его характер.
.
В случае разрыва указать его характер.
26.4.
Исследовать на непрерывность функцию
![]() .
В случае разрыва указать его характер.
.
В случае разрыва указать его характер.
26.5.
Исследовать на непрерывность функцию
![]() .
В случае разрыва указать его характер.
.
В случае разрыва указать его характер.
26.6.
Исследовать на непрерывность функцию
![]() .
В случае разрыва указать его характер.
.
В случае разрыва указать его характер.
26.7.
Исследовать на непрерывность функцию
![]() .
В случае разрыва указать его характер.
.
В случае разрыва указать его характер.
3. Дифференциальное исчисление функций одной переменной.
Занятие № 27.
Дифференцирование функций. Геометрический смысл производной.
27.1. Используя определение производной, найти производные следующих функций:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
27.2. Используя правила дифференцирования, найти производные следующих функций:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() ;
;
и)
![]() ;
;
к)
![]() .
.
27.3. Используя метод логарифмического дифференцирования, найти производные функций
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
27.4.
Составить уравнения касательной и
нормали к графику функции
![]() в точке с абсциссой
в точке с абсциссой
![]() .
.
27.5.
Составить уравнение касательной к
графику функции
![]() ,
перпендикулярной прямой
,
перпендикулярной прямой
![]() .
.
27.6.
Составить уравнение касательной к
графику функции
![]() ,
проходящей через точку
,
проходящей через точку
![]() .
.
27.7.
Найти угол между параболами
![]() и
и
![]() в точке их пересечения.
в точке их пересечения.
27.8.
Составить уравнение касательной к
графику функции
![]() ,
параллельной прямой, проходящей через
точки (1;7) и (-2;-2).
,
параллельной прямой, проходящей через
точки (1;7) и (-2;-2).
27.9.
Найти производные гиперболических
функций
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
27.10. Найти производные неявных функций
а)
![]()
б)
![]()
в)
![]()
г)
![]()
27.11.
Найти производные функций
![]() ,
заданных параметрически
,
заданных параметрически
а)
![]()
б)
![]()
в)
![]()
г)
![]()
Занятие № 28.
Дифференциал и его применение в приближенных вычислениях.
28.1. Найти дифференциалы функций
а)
![]()
б)
![]()
в)
![]()
г)
![]()
28.2. Найти приближенно изменение функции
а)
![]() ,
а
,
а
![]() меняется
от 100 до 101
меняется
от 100 до 101
б)
![]() ,
а
меняется
от
,
а
меняется
от
![]() до
до
![]()
в)
![]() ,
а
меняется
от 2 до 1,98
,
а
меняется
от 2 до 1,98
г)
![]() ,
а
меняется
от
,
а
меняется
от
![]() до
до
![]()
д)
![]() ,
а
меняется
от 1 на 0,2
,
а
меняется
от 1 на 0,2
28.3. Вычислить приближенно
а)
![]()
б)
![]() ,
если
,
если
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
з)
![]()
28.4. С какой точностью может быть вычислен объем шара, если его радиус измерен с точностью до 1%?
Занятие № 29.
Производные и дифференциалы высших порядков. Формула Тейлора.
29.1.
Найдите производную 4-го порядка от
функции
![]()
29.2. Найдите производные 2-го порядка функций
а)
![]()
б)
![]()
в)
![]()
29.3. Найти производные 2-го порядка от функций, заданных параметрически
а)
![]()
б)
![]()
29.4. Найти производные n-го порядка функций
а)
![]()
б)
![]()
в)
![]()
29.5. Найти вторые дифференциалы функций
а)
![]()
б)
![]()
в)
![]()
29.6.
Найти третий дифференциал функции
![]()
29.7. Разложить по формуле Тейлора (до степени не ниже 3-й) функции:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
з)
![]()
и)
![]()
к)
![]()
29.8. Вычислить приближенно с точностью до 0,0001
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
Занятие № 30.
Правило Лопиталя.
30.1. Используя правило Лопиталя, найти пределы:
а)
![]()
б)
![]()
в)
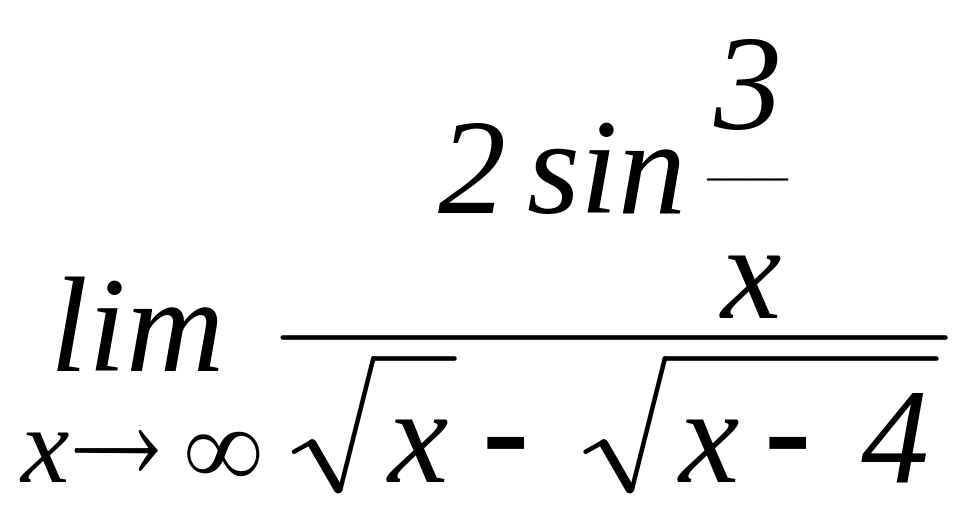
г)
![]()
д)
![]()
е)
![]()
ж)
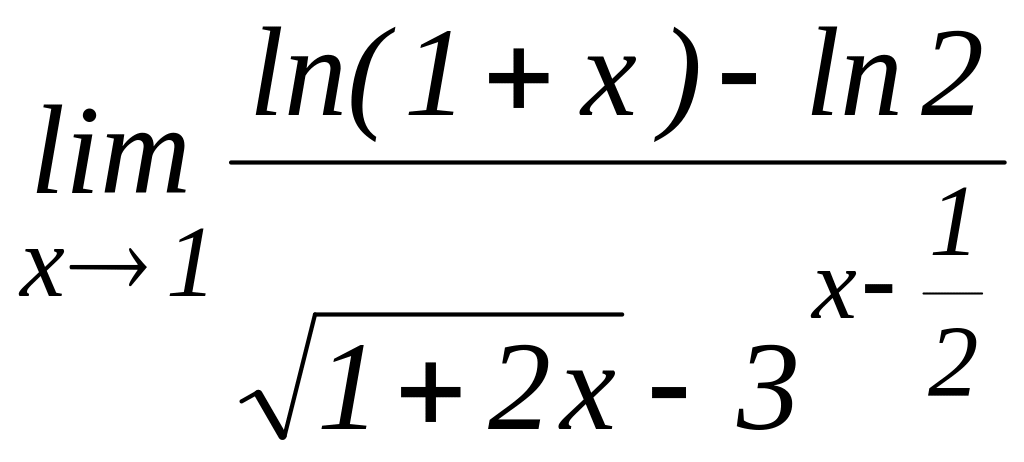
з)
![]()
и)
![]()
к)
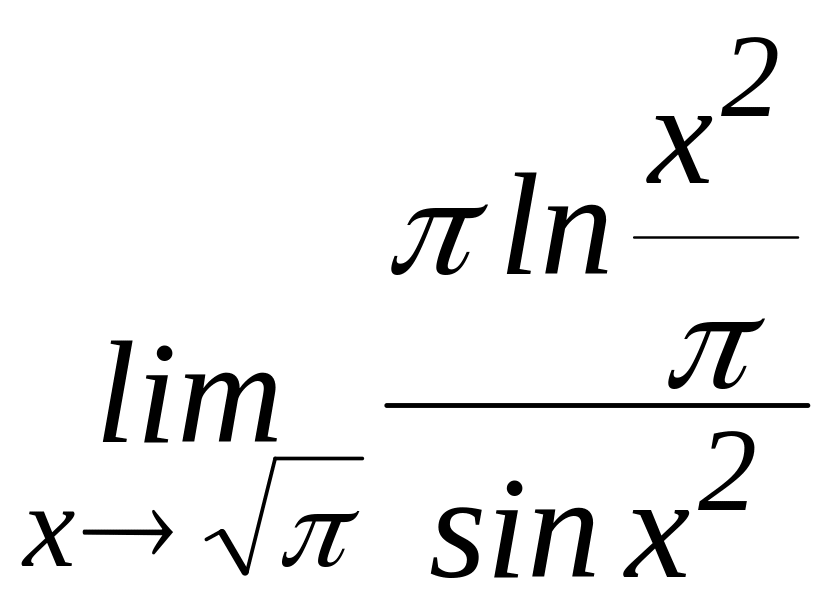
30.2. Используя правило Лопиталя, найти пределы:
а)
![]()
![]()
б)
![]()
в)![]()
г)
![]()
д)
![]()
30.3. Используя правило Лопиталя, найти пределы:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
Занятие № 31.
Исследование функции на монотонность и экстремум
с помощью первой производной.
31.1. Найти интервалы монотонности и экстремумы функций
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
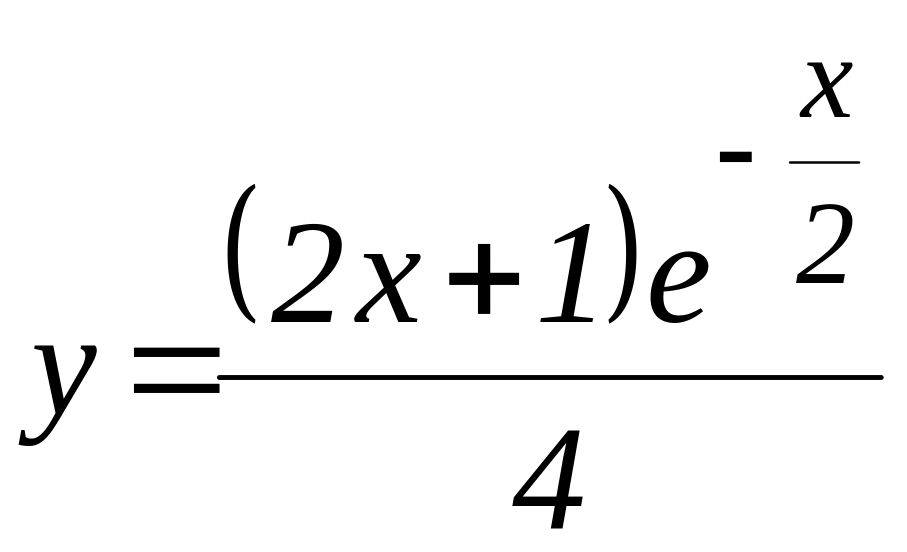
е)
![]()
ж)
![]()
з)
![]()
и)
![]()
к)
![]()
31.2. Найти наибольшее и наименьшее значение функций на заданных отрезках
а)
![]()
![]()
б)
![]()
![]()
в)
![]()
![]()
г)
![]()
![]()
д)
![]()
![]()
31.3. Рассматриваются всевозможные прямоугольные параллелепипеды, основания которых являются квадратами, а каждая из боковых сторон имеет периметр, равный 6 см. Найти среди них параллелепипед с наибольшим объемом и найти этот объем.
31.4. Определить размеры открытого бассейна с квадратным дном, при которых на облицовку стен и дна пойдет наименьшее количество материала. Объем бассейна V фиксирован.
31.5. Требуется огородить два участка: один – в форме правильного треугольника, другой – в форме полукруга. Длина изгороди фиксирована и равна Р. Определить размеры участков (строну треугольника и радиус полукруга) так, чтобы сумма площадей этих участков была бы наибольшей.
31.6. В треугольнике с основанием а и радиусом h вписан прямоугольник, основание которого лежит на основании треугольника, а две вершины – на боковых сторонах. Найти наибольшую площадь вписанного прямоугольника.
Занятие № 32.
Исследование функции на выпуклость и наличие точек перегиба
с помощью производной второго порядка.
32.1. Найти точки перегиба и интервалы выпуклости функций
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
з)
![]()
и)
![]()
к)
![]()
Занятие № 33.
Асимптоты графиков функций.
33.1. Найти асимптоты графиков функций
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
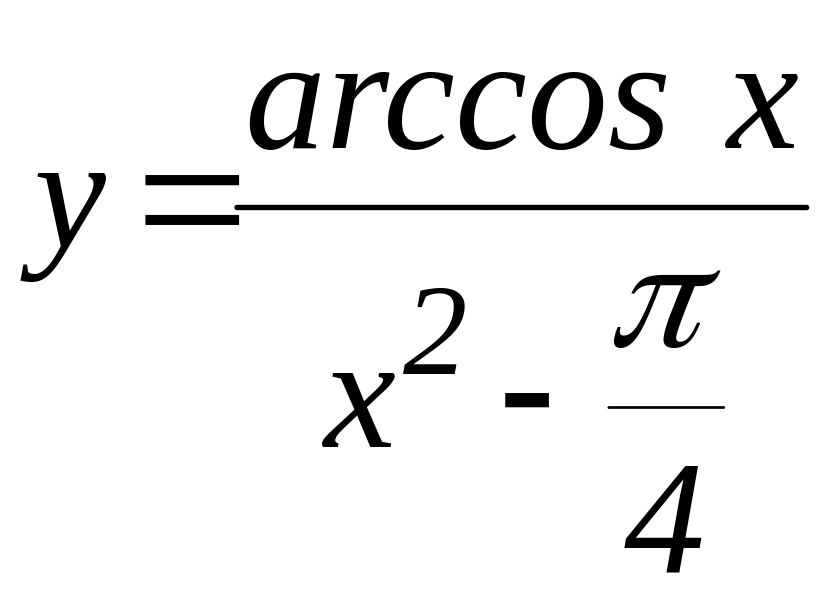
е)
![]()
ж)
![]()
з)
![]()
Занятие № 34.
Общая схема исследования функций и построения графиков.
34.1. Исследовать функции и построить их графики
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
з)
![]()
и)
![]()
к)
![]()
л)
![]()
м)
![]()
34.2. Исследовать функции и построить их графики
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
з)
![]()
и)
![]()
к)
![]()
л)
![]()
м)
![]()
