Занятие № 12. Прямая на плоскости.

12.1. Вычислить угловой коэффициент k прямой, проходящей через две точки А(5, -3) и В(-1, 6).

12.2. Составить уравнение прямой, параллельной двум прямым , и проходящей посередине между ними.

12.3. Дана прямая . Составить уравнение прямой, проходящей через точку А(2, 1) параллельно данной прямой.

12.4. Дана прямая . Составить уравнение прямой, перпендикулярной к данной прямой и проходящей через точку А(2, 3).

12.5. Даны уравнения двух сторон прямоугольника , и уравнение одной из его диагоналей . Найти вершины прямоугольника.

12.6. Вычислить величину отклонения  и расстояние d точки А(-2, 3) от прямой .

12.7. Привести общее уравнение прямой к нормальному виду.

12.8. Даны вершины треугольника: А(-10, -13), В(-2, 3) и С(2, 1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.

12.9. Установить, лежат ли точка Р(1, -3) и начало координат по одну или по разные стороны прямой .

12.10. Даны две смежные вершины квадрата А(2, 0) и В(-1, 4). Составить уравнение его сторон.

12.11. Составить геометрическое место точек, равноудаленных от параллельных прямых и .

12.12. Составить уравнение прямой, проходящей через точку А(2, 3) и отсекающей на координатных осях отрезки равной длины, считая каждый отрезок от начала координат.

12.13. Найти угол между двумя прямыми:

а) и ;

б) и .

12.14. Найти уравнение прямой, проходящей через начало координат и образующей с прямой у = 2х - 4 угол 45°.

12.15. Дан треугольник с вершинами А(7,0), В(3,-4), С(2,3). Найти уравнения стороны АВ, высоты CD, биссектрисы BE, медианы CF.

Занятие № 13. Кривые второго порядка.

13.1. Составить уравнение окружности, касающейся двух параллельных прямых: , , причем одной из них – в точке А(2, 1).

13.2. Составить уравнение окружности, касающейся осей координат, если центр окружности лежит в точке с координатами .

13.3. Дана окружность . Из ее точки А(2,0) проведены всевозможные хорды. Определить геометрическое место середин этих хорд.

13.4. Дан эллипс найти:

1. его полуоси,

2. фокусы,

3. эксцентриситет,

4. уравнение директрис.

13.5. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что

1) его полуоси равны 3 и 2;

2) его малая ось равна 24, а расстояние между фокусами 2с=10.

3) его большая ось равна 20, а расстояние между фокусами 2с=12,

4) его малая полуось равна 10, а эксцентриситет ,

5) его большая ось равна 20, а эксцентриситет .

6) расстояние между его директрисами равно 10 и расстояние между фокусами 2с=8,

7) его большая ось равна 8, а расстояние между директрисами равно 16,

8) его малая ось равна 4 расстояние между директрисами равно 10,

9) расстояние между его директрисами равно 16 и .

13.6. Найти острый угол между асимптотами гиперболы .

13.7. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, зная, что

1) ее оси 2а=4 и 2b=6,

2) расстояние между фокусами 2с=16 и ось 2b=12,

3) расстояние между фокусами 2с=6 и эксцентриситет ,

4) расстояние между директрисами равно и расстояние между фокусами 2с = 26;

5) расстояние между директрисами равно и эксцентриситет ;

6) расстояние между директрисами равно , а уравнения асимптот имеют вид .

13.8. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси и ее параметр р=3.

13.9. Составить уравнение параболы, которая имеет фокус F (0,-3) и проходит через начало координат, зная, что ее осью служит ось .

13.10. Найти координаты фокуса параболы:

1. ;

2. ,

3. ;

4. .

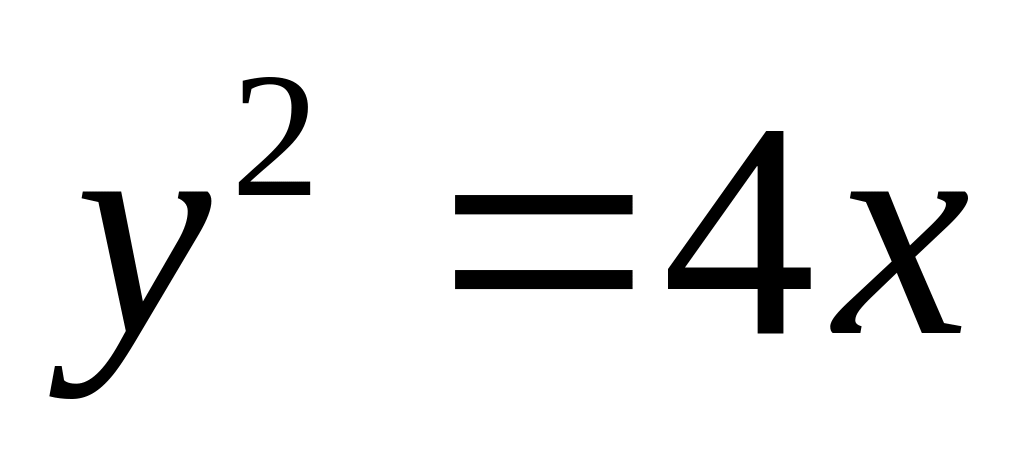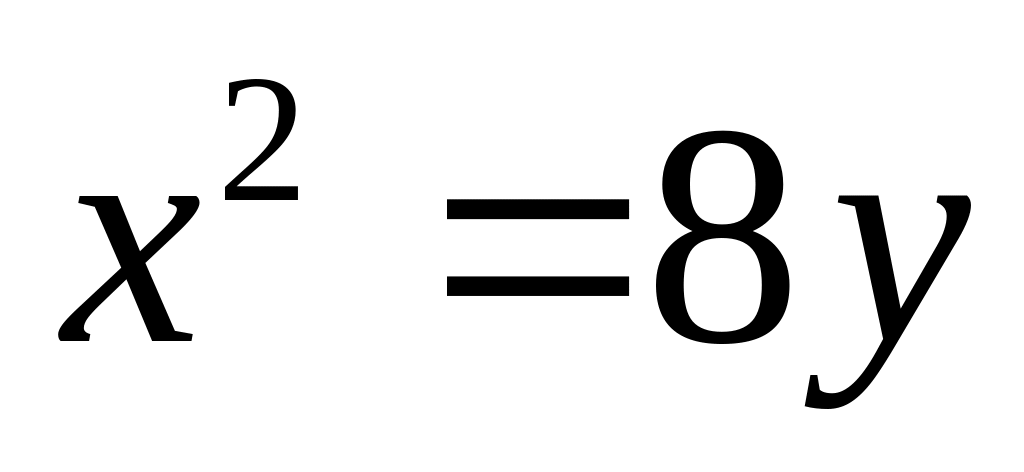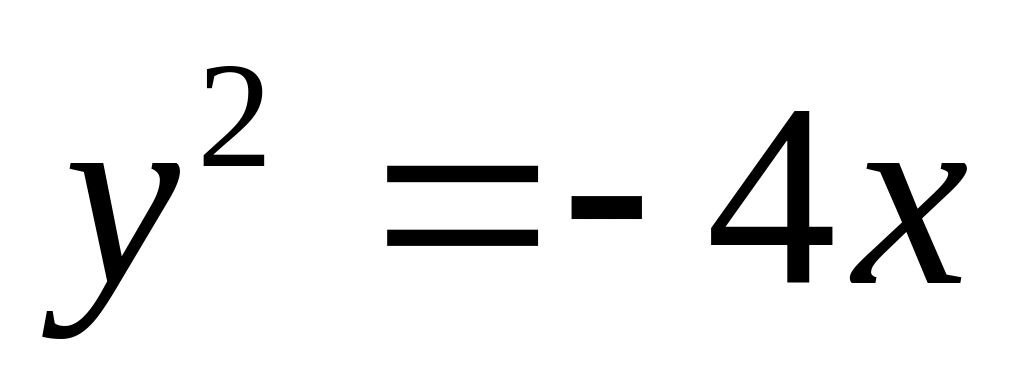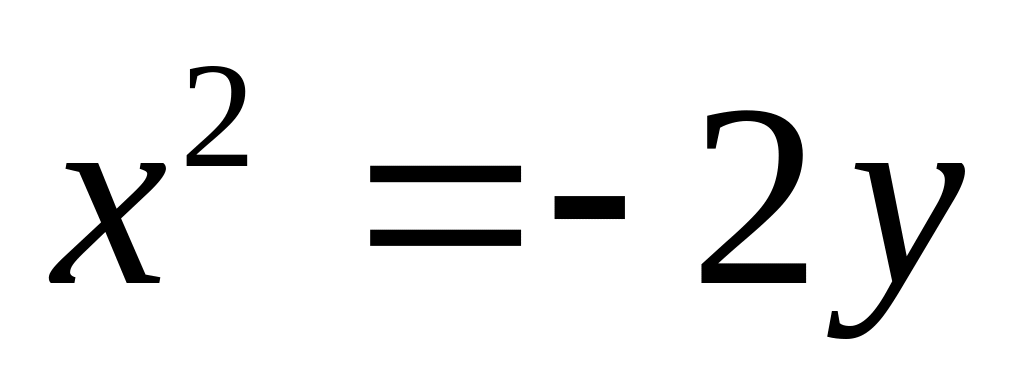13.11. Найти вершину, фокус, ось и директрису параболы .