1.4. Методика расчета магнитной цепи по коэффициентам рассеяния

Прямая задача. Дана величина магнитной индукции В_н для _н, необходимо определить намагничивающую силу катушки _к (рис. 2,а). (Геометрические размеры магнитопровода заданы; зазор е₂=0).

а) Определяют G_н, G_ен, g_s и коэффициенты рассеяния

_х2 и _х3.

б) Находят величины магнитных потоков

₁ = _н_х1 = _н; ₂ = _н_х2; ₃ = _н_х3 и магнитных индукций:

(15)

в)Определяют напряженность Н, А/м по значениям индукции В на каждом участке, используя кривую намагничивания стали (рис.3). Для каждого участка определяют падение магнитного потенциала на нем, то есть U_мя = Iw_я = Н_стяl_я; U’_{м ст1} = Н_ст1l₁ … Намагничивающая сила катушки _к определяется по II закону Кирхгофа как сумма падений магнитного потенциала по замкнутому контуру рабочего потока _

_к = (Iw)_ + (Iw)_e + (Iw)_я + (Iw)_ст1 + (Iw)’_ст1 +(Iw)_ст2 + (Iw)’_ст2 +­­ ­­(Iw)_ст3,(16)

г де

Если сечения ярма и сердечника равны S₁ = S’_1, то В_ст1 = В’_ст1 и В_ст2 = В’_ст2.

Обратная задача: определение величин магнитных потоков при заданной намагничивающей силе катушки решается методом последовательных приближений. В случае решения обратной задачи для _i после решения прямой задачи для _н необходимо сначала делать расчет обмотки электромагнита (см. следующий параграф) для уточнения

д ействительной величины намагничивающей силы и

проверки теплового режима обмотки.

а) Для выбранного положения якоря _i находят G_; G_е и соответтственно коэффициенты рассеяния _{х2 ­} и _х3.

б) Без учета сопротивления стали магнитный поток расчетный _р равен

_iр = _кG_{i ,}

где G_i – суммарная проводимость всех воздушных зазоров по контуру

рабочего потока для данного i-го положения якоря.

В действительности из-за сопротивления стали _i  _iр, т. е.

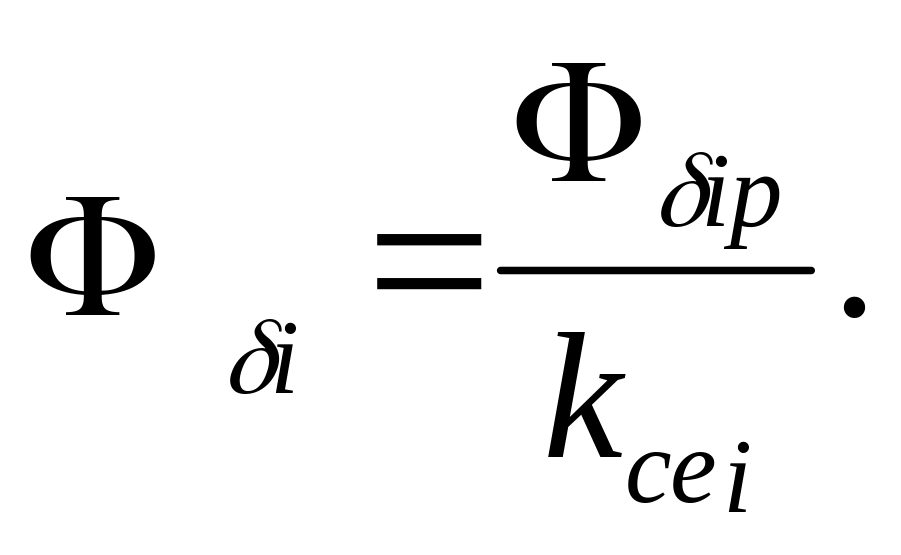
Здесь k _стi – коэффициент, учитывающий сопротивление стали, k_ст  1, его величина изменяется при движении якоря. Если _н  _ср  _к, то k_{ст и}  k_{ст ср}   k_{ст к.}

Задаваясь величиной _i , решают прямую задачу расчета магнитной цепи, т. е. определяют необходимую для выбранного потока намагничивающую силу катушки ’_к с учетом сопротивления стали и потоков рассеяния. Если ’_к ≥≤ _к, то задаются другим значением магнитного потока _i и определяют ’’_к. Действительный поток _i находят графическим построением (рис. 4), либо следующим приближением.

1.5. Расчет обмотки электромагнита

Из расчета магнитной цепи при заданном рабочем потоке _ была определена необходимая намагничивающая сила обмотки _к; ;если дана величина напряжения питания, то можно рассчитать необходимый диаметр провода и число витков обмотки [3].

Геометрия магнитной цепи дает максимальные размеры каркаса обмотки, обмоточное окно катушки Q_к = h_кl_к меньше всей площади окна Q = hl_, примерно Q_к = (0,8–0,9)Q.

Диаметр голого провода d , мм может быть найден следующим образом:

(17)

(18)

Решая совместно уравнения (17) и (18), найдем

, (19)

где l_ср – длина среднего витка, м;

_ – удельное сопротивление обмотки при нагреве до температуры _н, Оммм²/м:

_ = ₀(1+_н) . (20)

Здесь  = 0,004 1/⁰С,

_ =0,0162 Оммм²/м при ₀ = 0⁰С.

Определив диаметр голого провода d из уравнения (19), округляя его в сторону увеличения, необходимо по ГОСТу (табл. 4) подобрать провод, то есть, выбрать d и d (диаметры голого и изолированого провода). В табл. 4 проведены средние значения коэффициенты заполнения обмотки по меди k_3м и удельное число витков w₀ = w/Q_к для провода марки ПЭЛ. Коэффициент заполнения обмотки по меди k_3м определяет отношение площади поперечного сечения меди всех витков обмотки Q_к:

(21)

число витков обмотки w определяется:

(22)

По уравнению (18) определяется сопротивление обмотки R, а по уравнению (17) д ействительная намагничивающая сила катушки