
- •Понятие вероятности и классическое определение вероятности.
- •Некоторые элементы комбинаторики
- •Условная вероятность. Формула умножения вероятностей.
- •Формула Байеса
- •Аксиоматическое построение теории вероятностей
- •Последовательность независимых испытаний (схема Бернулли)
- •Случайные величины и функции распределения
- •Ф ункция распределения случайных величин
- •Плотность распределения случайной величины
- •Числовые характеристики случайных величин
- •Момент, дисперсия, среднеквадратичное отклонение
- •Зависимые и независимые случайные величины
- •Система произвольного числа случайных величин
- •Законы распределения и числовые характеристики функции случайных величин
- •Теоремы о числовых характеристиках
- •Закон распределения монотонной функции одного случайного элемента.
- •Предельные теоремы теории вероятностей
- •Закон больших чисел в форме теоремы Чебышева
- •Обобщённая теорема Чебышева и теорема Маркова
- •Характеристические функции
- •Основные свойства характеристических функций
- •Центральная предельная теорема для суммы одинаково распределённых слагаемых
- •Математическая статистика
- •Весовые характеристики статистического распределения
- •Доверительный интервал
- •Проверка статистических гипотез
- •Метод наименьших квадратов
Плотность распределения случайной величины
Рассмотрим
![]() .
Средняя вероятность на единицу длины
на отрезке
.
Средняя вероятность на единицу длины
на отрезке
![]() .
.
Производная функции распределения называется плотностью распределения или плотностью вероятности или дифференциальным законом распределения.
Свойства плотности вероятности:
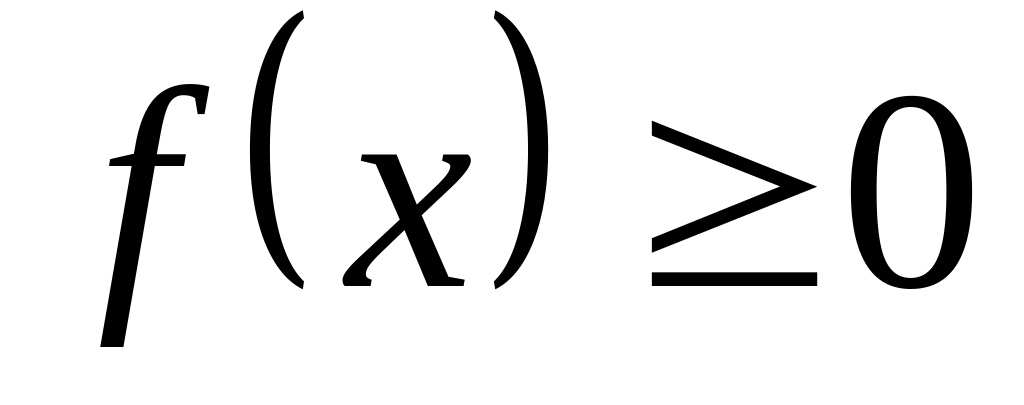 .
.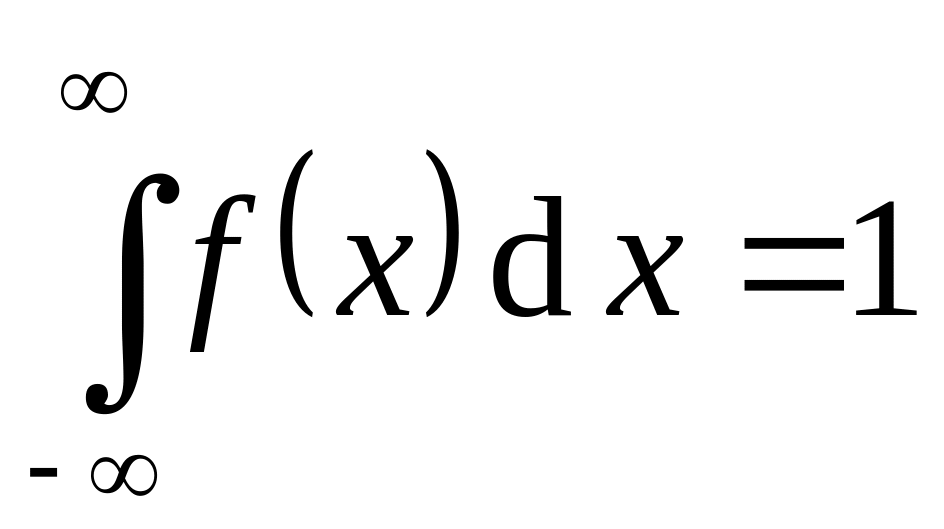 .
.
![]() .
.
Числовые характеристики случайных величин
Характеристики положения: математическое ожидание, мода, медиана.
Если задан ряд:
x |
|
|
… |
|
p |
|
|
… |
|
то математическое ожидание
![]() .
Для непрерывной величины
.
Для непрерывной величины
![]() .
.
Мода – координата локального максимума плотности вероятности.
М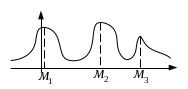 едиана
– такое число, что прямая
едиана
– такое число, что прямая
![]() делит площадь под функцией распределения
на две равные части, т.е.
делит площадь под функцией распределения
на две равные части, т.е.
![]() .
.
Момент, дисперсия, среднеквадратичное отклонение
Начальный момент k=го
порядка:
![]() .
Для непрерывного x:
.
Для непрерывного x:
![]() .
.
Видно, что
![]() .
.
Центральный момент k-го
порядка:
![]() .
Для непрерывного x:
.
Для непрерывного x:
![]() .
.
Видно, что
![]() .
.
Дисперсия
![]() .
.
Среднеквадратичное
отклонение
![]() .
.
Рассмотрим
![]() ;
;
![]() .
.
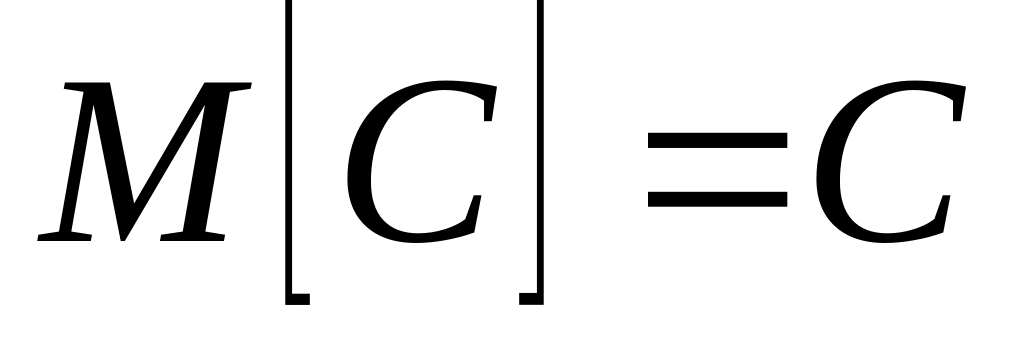 ,
где
,
где
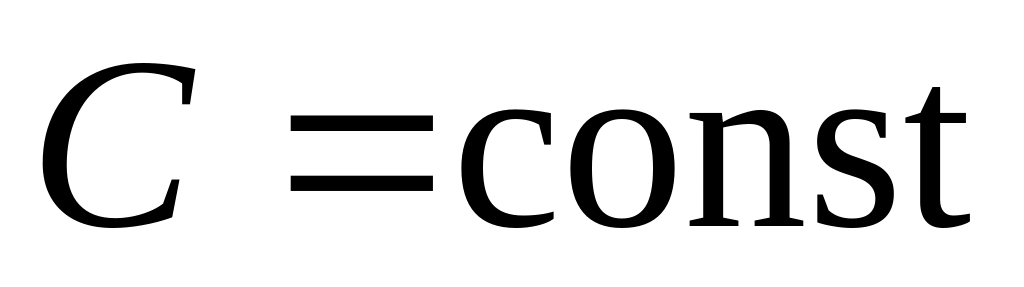 .
.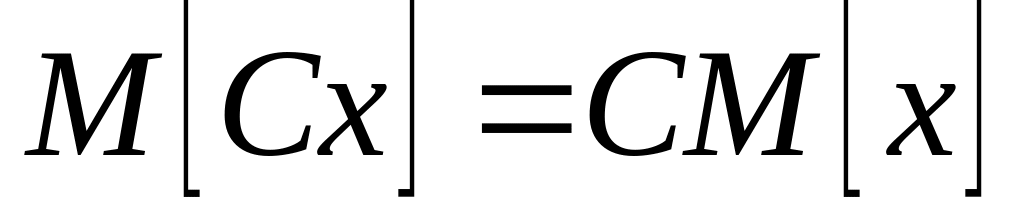 .
.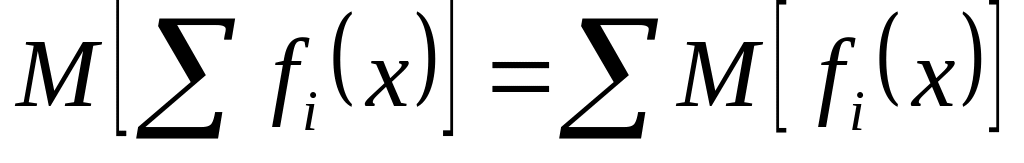 .
.
Величина
![]() называется коэффициентом
асимметрии.
называется коэффициентом
асимметрии.
Величина
![]() является характеристикой
крутизны кривой.
является характеристикой
крутизны кривой.
Для нормального распределения
![]() .
.
Некоторые известные законы распределения случайных величин.
Закон равномерной плотности или равномерного распределения
![]() .
Найдём C:
.
Найдём C:
![]() .
Таким образом,
.
Таким образом,
![]() .
.
![]()
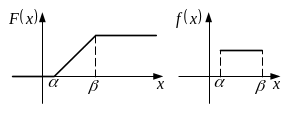 .
.
![]() .
Моды у этого распределения нет. Медиана
.
Моды у этого распределения нет. Медиана
![]() .
Дисперсия
.
Дисперсия
![]()
![]() .
Среднеквадратичное отклонение
.
Среднеквадратичное отклонение
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Нормальный закон распределения (закон Гаусса)
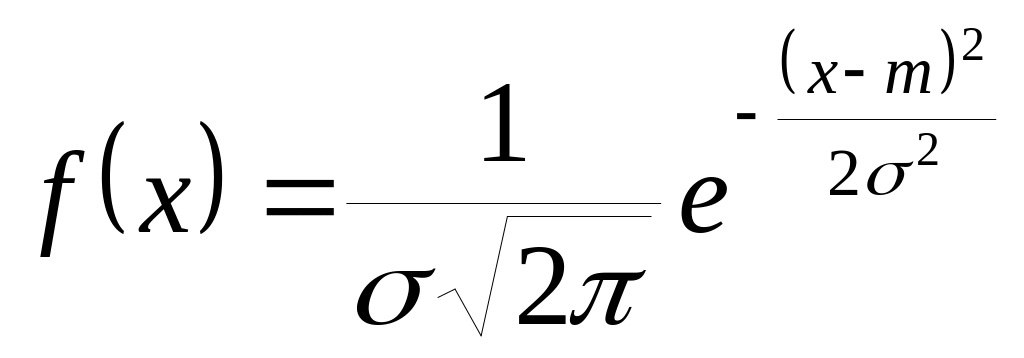 ,
где и m
– параметры распределения.
,
где и m
– параметры распределения.
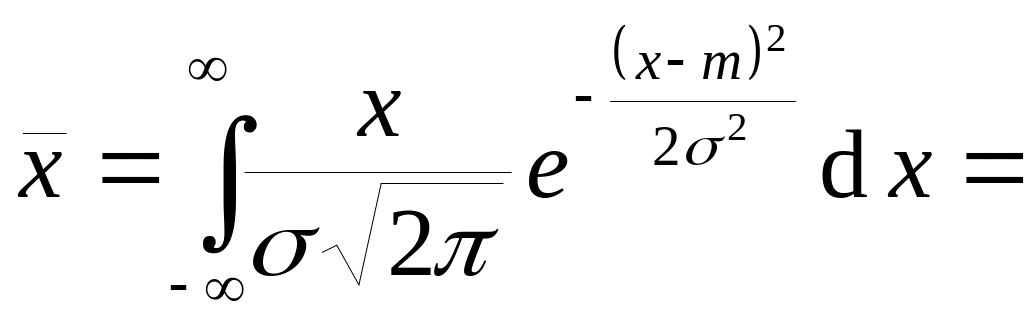
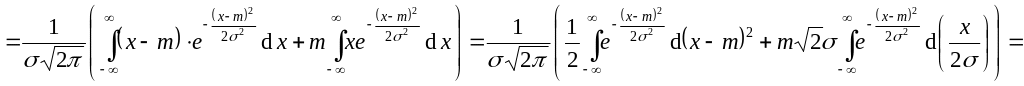
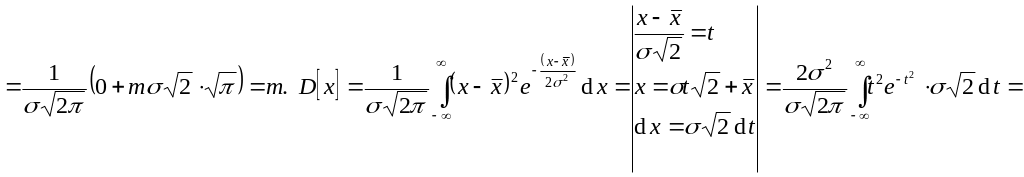
![]() .
Среднеквадратичное отклонение = .
.
Среднеквадратичное отклонение = .
Центральный момент k-го
порядка
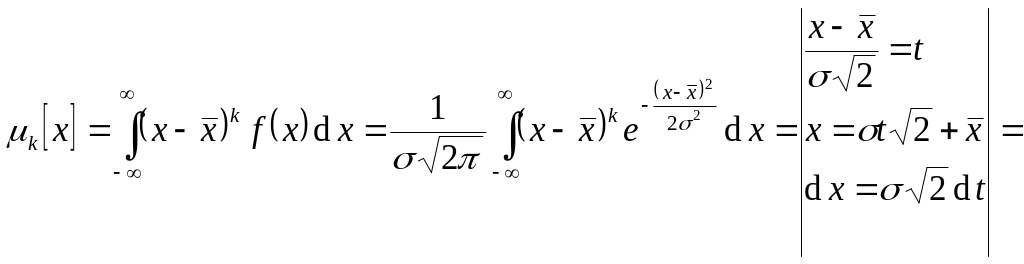
![]() .
Если k – нечётное, то
.
Если k – нечётное, то
![]() ,
иначе
,
иначе
![]()
![]() .
.
Отсюда следует, что
![]() .
Эксцесс
.
Эксцесс
![]() ,
что, собственно, следует из его
определения.
,
что, собственно, следует из его
определения.
Показательное распределение
![]() .
.
![]()
![]()
![]()
![]() .
.
Закон (распределение) Пуассона:
Если задана случайная
дискретная величина
![]() ,
то вероятность того, что
,
то вероятность того, что
![]() .
.
Многоугольник распределения:
![]()
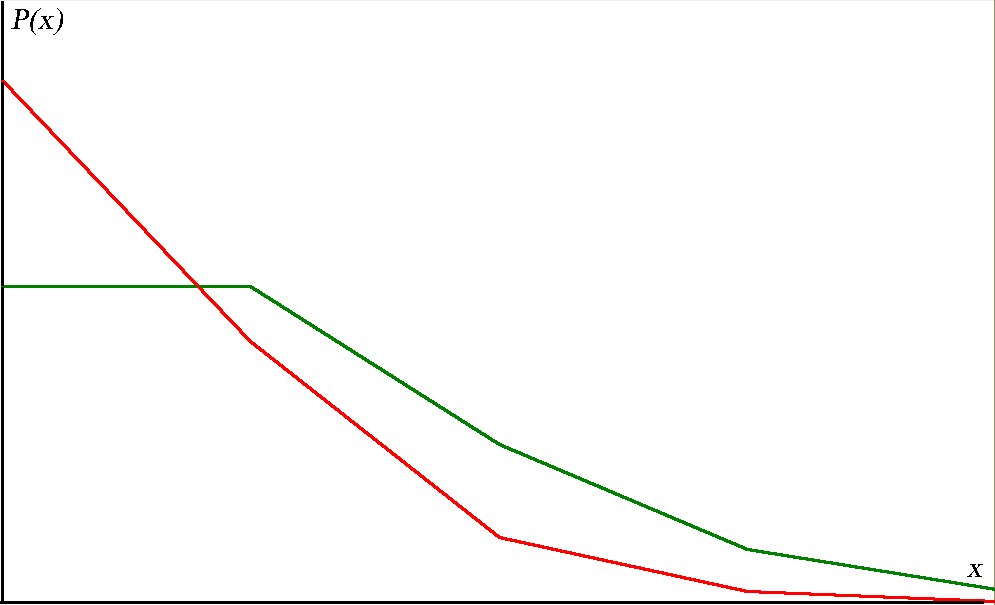
![]()
![]()
![]() .
.
Биномиальное распределение:
![]() .
.
![]()
![]() (бином Ньютона)
(бином Ньютона)
![]()
![]()
![]() .
.
Системы случайных величин или многомерные случайные величины
Ф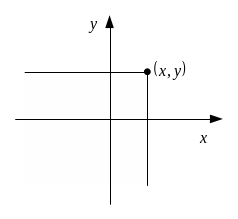 ункцией
распределения двух случайных величин
называют вероятность выполнения двух
неравенств:
ункцией
распределения двух случайных величин
называют вероятность выполнения двух
неравенств:
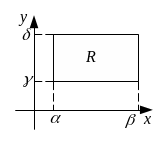
![]() ,
т.е. вероятность попадания в заштрихованную
область.
,
т.е. вероятность попадания в заштрихованную
область.
Свойства двумерных функций распределения:
Если
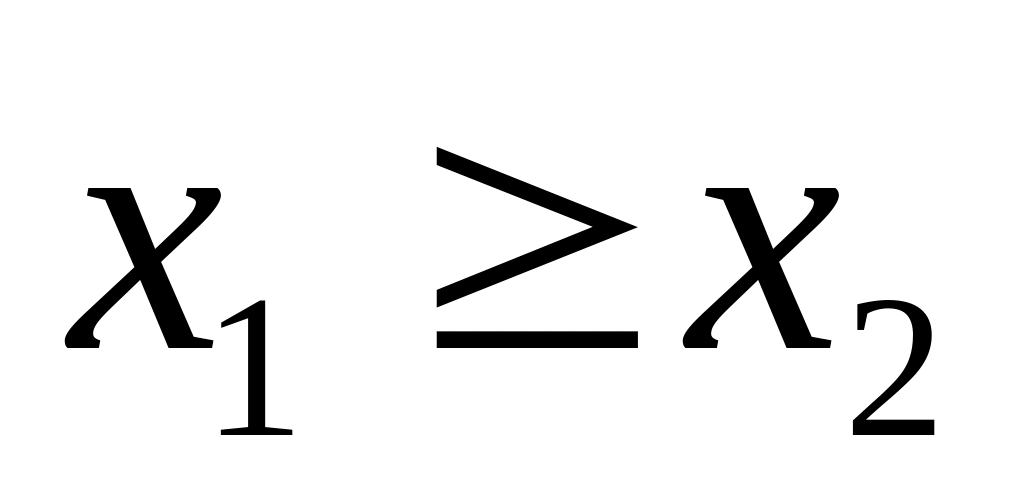 ,
то
,
то
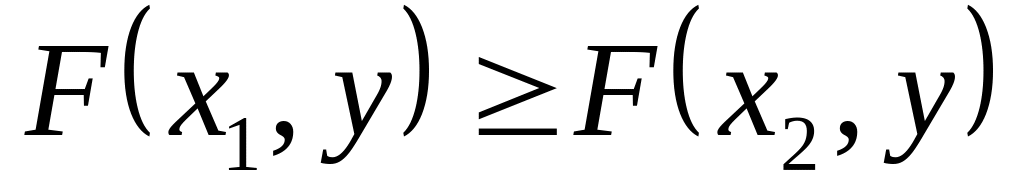 ,
если
,
если
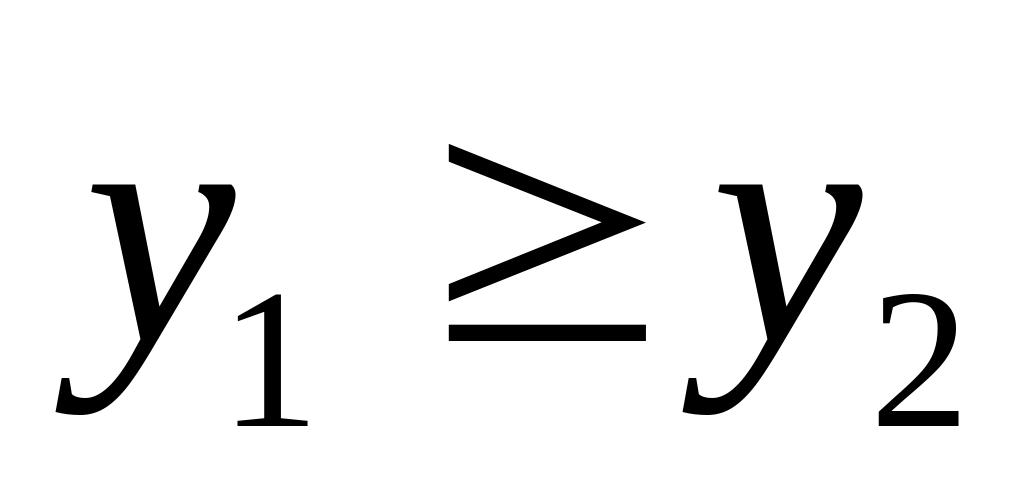 ,
то
,
то
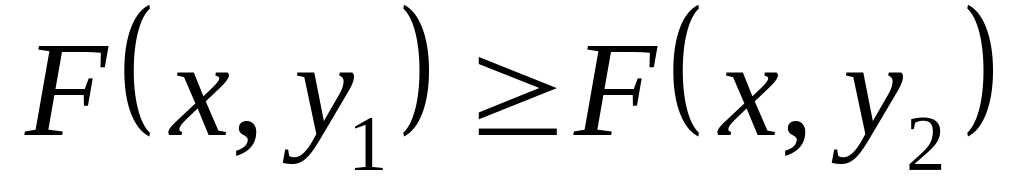 .
.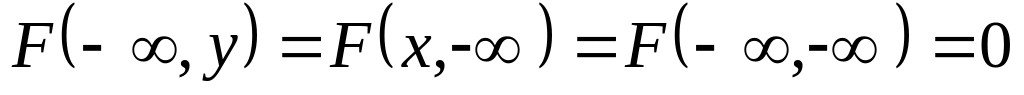 .
.Одномерные функции можно представить через двумерные:
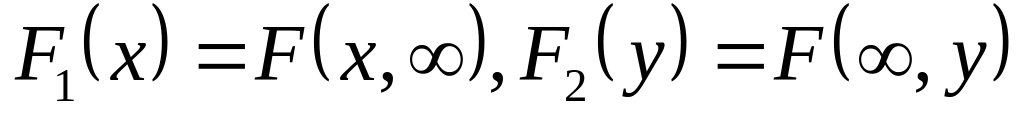 .
.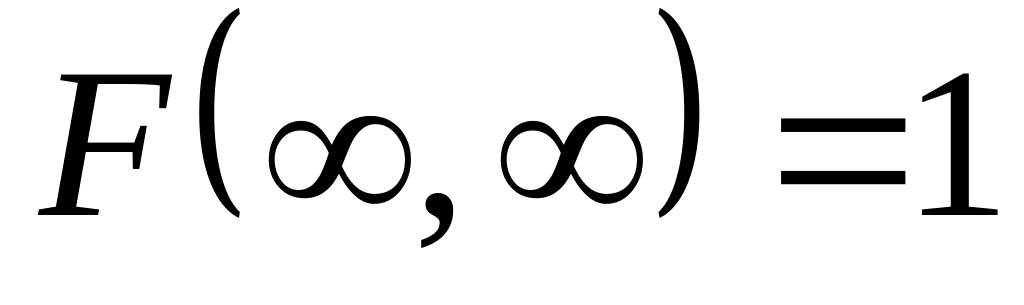 .
.
![]() .
.
Вероятность попадания в
прямоугольник со сторонами
![]() и
и
![]() будет:
будет:
![]() .
Тогда вероятность попадания в какую-то
область
.
Тогда вероятность попадания в какую-то
область
![]() .
Функция
.
Функция
![]() – плотность распределения.
– плотность распределения.
Плотности распределения отдельных величин, входящих в систему случайных величин. Условные законы распределения.
Пусть заданы функции распределения
![]() и
и
![]() .
Тогда
.
Тогда
![]() ,
,
![]() где
где
![]() – функция плотности распределения для
– функция плотности распределения для
![]() .
Тогда
.
Тогда
![]() .
.
Условным законом распределения
величины x,
входящих в систему
![]() называется её закон распределения,
вычисленный при условии, что другая
величина Y
приняла определённое значение y.
называется её закон распределения,
вычисленный при условии, что другая
величина Y
приняла определённое значение y.
Вероятность попадания в прямоугольник
со сторонами
и
![]()
![]() где
где
![]() и
и
![]() – два события. Тогда
– два события. Тогда
![]()
![]() .
Следовательно,
.
Следовательно,
![]()
![]() Таким образом,
Таким образом,
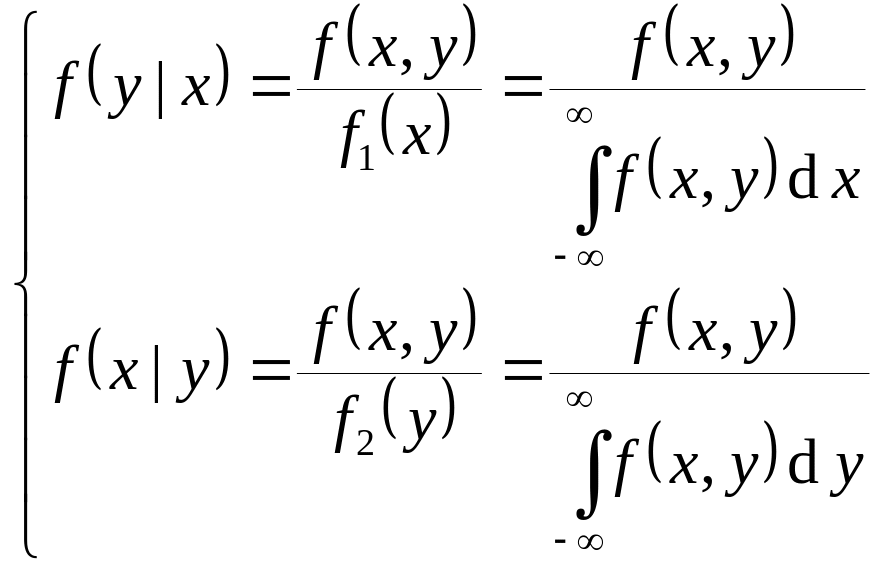 .
.
Двумерный ряд распределения:
X Y |
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
… |
|
|
|
… |
|
![]() .
При этом
.
При этом
![]() (сокращённо)
(сокращённо)
![]()
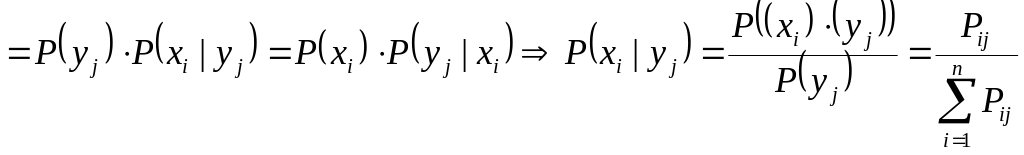 .
.
