Глава 4Числовые характеристики случайных величин.

4.1Роль и назначение числовых характеристик. Математическое ожидание случайной величины.

Выше мы привели законы распределения, среди них функция распределения и ряд распределения для дискретных величин, которые почти полностью описывают вероятность с. в.

Но не всегда возможно, а иногда просто нет надобности сложных вычислений ф. р., чтобы описать разброс той или иной с. в. Часто достаточно воспользоваться какими – либо числами, характеризующими с. в. (например: среднее или что – нибудь типа,, степени случайности,,)

Опр. Числовыми характеристиками с. в. называются числа, способные выразить в сжатой форме наиболее существенные черты распределения.

Умение применять теорию вероятностей для решения практических задач в значительной мере определяется искусством пользоваться числовыми характеристиками случайных величин, оставляя в стороне законы распределения.

Опр. Характеристика положения - это определённая числовая характеристика с. в., описывающая её положение на числовой оси.

Одна из таких характеристик положения есть математическое ожидание (иногда её называют просто средним значением)

Опр. Математическим ожиданием дискретной с. в. называется сумма произведение всех возможных её значений на вероятности этих значений.

т.к. 

Для бесконечного числа элементов дискретной с. в.:

Сложность здесь может возникнуть, если ряд не будет сходиться.

Для не дискретной с. в. (из определения интеграла):

Для частотной модели:

n количество опытов

с. в. Х { x_1, x₂, …, x_n}

n_i - выпадение x_i значения

Среднее арифметическое есть:

Но n_i/n - есть частота р_i^*, т. е.

А известно, что при увеличении n р_i^* приближается к p_i.

Так же существуют и другие характеристики положения.

Опр. Модой с. в. называется её наиболее вероятное значение (то, для которого вероятность p_i или плотность распределения f(x) достигает максимума).

Опр. Если вероятность или плотность вероятности достигают не в одной, а в нескольких точках, то распределение называется полимодальным

Опр. Медианой непрерывной с. в. называется такое её значение x_m, для которого P{X<x_m} = P{X>x_m}=1/2

Пример 1: Найти мат. ожидание и моду для дискретной с. в. Х, имеющей ряд распределения:

X:	0	1	2	3
	0.1	0.3	0.5	0,1

Решение:

M[X] = 0*0,1+1*0,3+

+2*0,5+3*0,1=1,6

Мода с. в. Х М_х=2

Пример 2: Непрерывная с. в. имеет плотность f(x)=(sin x)/2 при х(0, ).

Найти мат. ожидание, моду и медиану х_m с. в. Х.

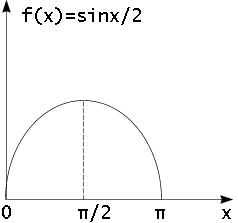
Решение:

Мода: M_х=/2

Медиана: т. к. пощади слева и справа от точки /2 равны, то х_m =/2

4.2 Моменты. Дисперсия. Среднее квадратичное отклонение.

Опр. Начальным моментом S –го порядка с. в. Х называется мат. ожидание S^ой степени этой величины:

Или

А для непрерывной с. в.:

Мат. ожидание - есть начальный момент первого порядка.

Опр. Центрированной с. в. называется отношение с. в. от её мат. ожидания:

Опр. Центральным моментом порядка S с. в. Х называется мат. ожидание S-ой степени центрированной с. в.:

Для дискретной с. в.:

Для непрерывной с. в.:

Центральный момент первого порядка:

Второго порядка:

Третьего порядка:

Аналогично:

Опр. Дисперсией с. в. есть мат. ожидание квадрата соответствующей центрированной величины:

Для дискретной с. в.:

Для непрерывной:

Замечание:

Дисперсия есть характеристика рассеивания, разбросанности с. в. около её мат. ожидания.

Опр. Средним квадратичным отклонением с. в. называется величина, равная квадратному корню из дисперсии:

Т ретий центральный момент характеризует асимметрию распределения:

- коэффициент асимметрии.

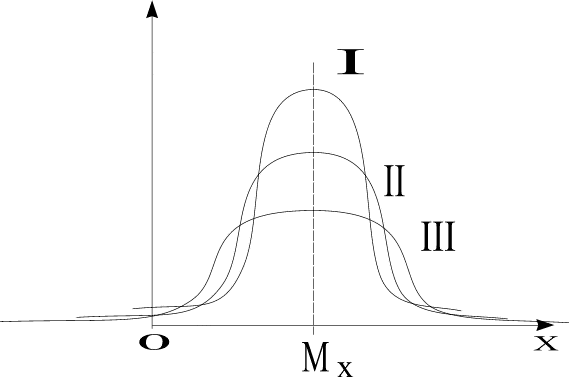
Четвёртый центральный момент ₄ служит характеристикой крутости.

Эксцесс:

Свойства мат. ожидания и дисперсии.

1) I) Математическое ожидание неслучайной величины С равно самой величине С:

М [С] = С

II) Дисперсия неслучайной величины С равна нулю:

D [C] = 0

2) I) При прибавлении к с.в. Х неслучайной величины С к её мат. ожиданию прибавляется та же величина:

M [ X+C] = M [ X ] + C

II) а её дисперсия не меняется:

D [ X+C ] = D [ X ]

3) I) При умножении с. в. Х на неслучайную величину С на ту же величину С умножается её мат. ожидание:

M [ C*X ] = C*M[ X ]

II) Дисперсия умножается на С²:

D [ C*X ] = C² M [ X ]