3.2Функция распределения случайной величины. Её свойства.

Опр. Функцией распределения с. в. называется вероятность того, что она примет значение меньшее чем заданное .

Геометрически функция распределения интерпретируется как вероятность того, что с. в. попадёт левее заданной т. .

Основные свойства функции распределения:

1). - неубывающая функция от своего аргумента, т. е. при

2).

3).

Доказательство:

Рассмотрим две точки

Возьмём событие где и

По правилу сложения несовместных событий (А и В)

или

а т. к.

Заключение:

Функция распределения любой с. в.есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1:

причём и

Вероятность попадания на участок через функцию распределения:

т. е. вероятность того, что с. в. Х в результате опыта попадёт на участок от до (включая ) равна приращению функции распределения на этом участке.

Выражение для вероятности отдельного значения с. в. через ф. р.

Замечание:

Значение этого предела зависит есть ли в т. у функции разрыв. Если нет, то предел равен 0. Если же есть, то предел равен высоте скачка.

3.3Функция распределения дискретной с. В. Индикатор события.

Зная ряд распределения дискретной с. в., легко построить ф. р., и обратно.

Возьмём к примеру следующий ряд распределения

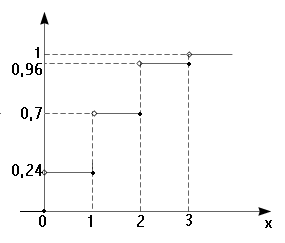
Построим для него функцию распределения.

0 < x  1

F(x)=P{X=0}=0.24

1 < x  2

F(x)=P{X<x}=P{x=0}+P{x=1}=

0.24+0.46=0.7

и так далее.

Ф. р. любой дискретной с. в. есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям с.в., и равны вероятностям этих значений.

Сумма всех скачков функции F(x) равна единице.

Опр. Индикатором события А называется случайная величина U, равная единице – если в результате опыта событие А произошло, и нулю - если не произошло.

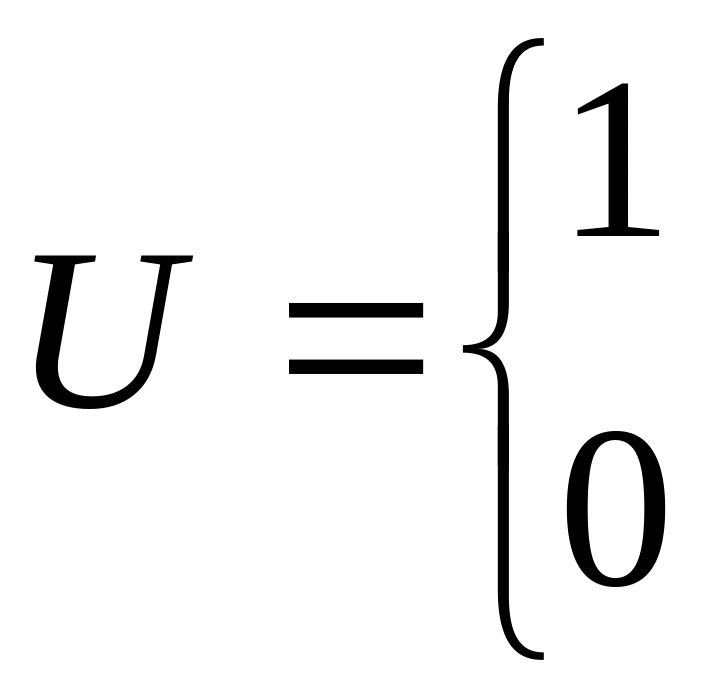
	если А произошло
	если А не произошло

Ряд распределения U:	0	1
	1-p	p

Где р – вероятность происхождения события А.

3.4Непрерывная случайная величина. Плотность распределения.

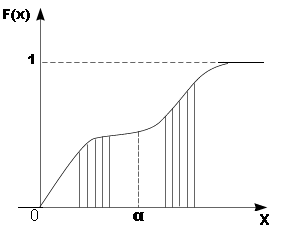
Разобьем непрерывную прямую на n прямоугольников  получаем дискретную функцию распределения  теперь устремим число n к бесконечности  переходим к непрерывной кривой  получаем P{x=} = 0

Опр. Непрерывной с.в. Х называется с.в., чья функция распределения непрерывна и дифференцируема.

Опр. Средней плотностью распределения на отрезке кривой функции распределения называется отношение вероятности попадания точки на этот отрезок к длине отрезка.

Опр. Плотностью распределения в точке  называется предел плотности на отрезке, содержащего точку , при стремлении обоих концов отрезка к точке , т.е. производная функции распределения в этой точке:

Опр. Кривой распределения называется график плотности распределения f(x).

Опр. Рассматриваем непрерывную с.в. Х с плотностью f(x) и элементарный участок dx, примыкающий к точке х.

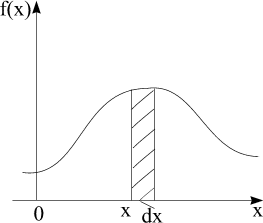
Опр. Вероятность попадания с.в. Х на этот участок dx равна f(x)dx. Эта величина f(x)dx называется элементом вероятности для точки х.

Теперь вероятность попадания с.в. Х на участок от  до  равна сумме элементов вероятности на всём этом участке, т.е.:

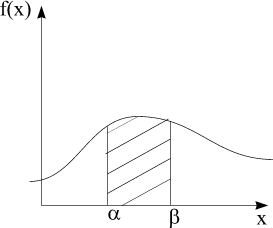
Если за один из концов отрезка мы возьмём - , то можем выразить функцию распределения:

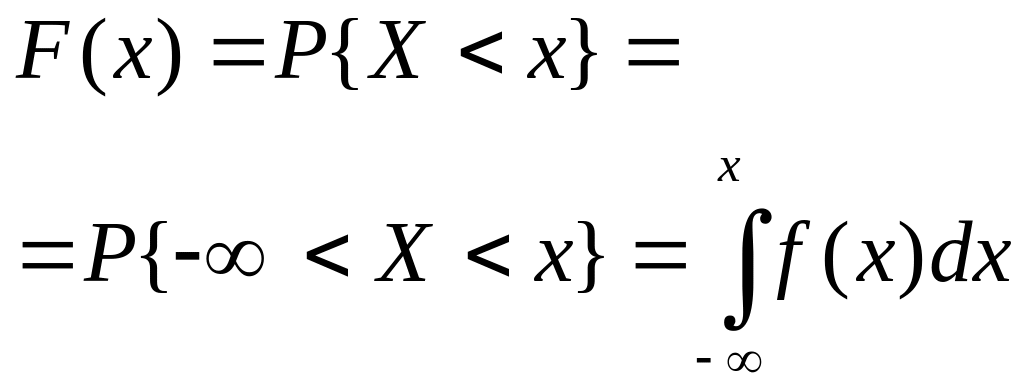
Основные свойства плотности распределения f(x):

1. Плотность распределения неотрицательная функция: f(x)  0

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

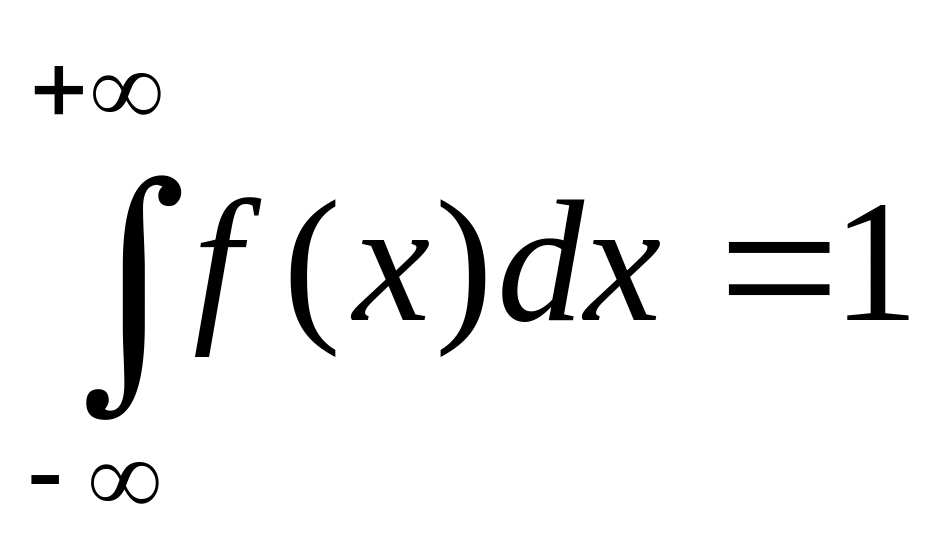
Доказательство:

Основные геометрические свойства интерпретируются так:

1. Вся кривая распределения лежит не ниже оси абсцисс.

2. Полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Вывод формулы полной вероятности и формулы Бейеса:

Пусть вероятность события А зависит от значения х с.в. Х с плотностью f(x).

Сделаем гипотезу, состоящую в том, что с.в. Х приняла значения, лежащие на элементарном участке dx, примыкающем к точке х.

В пределе Х=х

Обозначим - условная вероятность события А при Х=х

Интегральная формула полной вероятности:

Формула Бейеса:

Пусть до опыта с.в. Х имела плотность распределения f(x).

Произведён опыт, в результате которого появилось событие А.

Условная вероятность события А при Х=х обозначается .

Интегральная формула Бейеса:

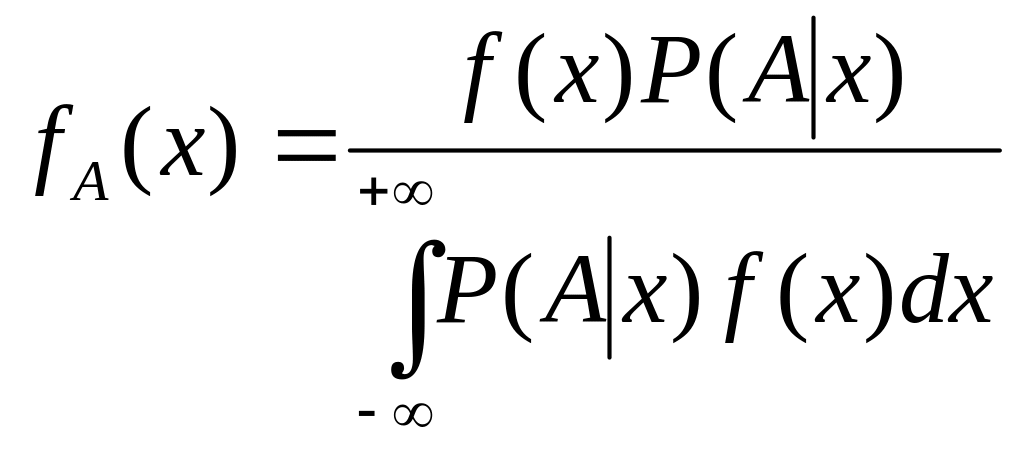
П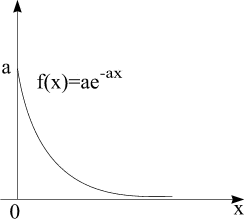 ример:

Плотность распределения с.в. Х – f(x)=ae^-ax (а  0) - показательное распределение.

1. Построить кривую распределения

2. Найти и построить ф. Р. с. в. Х

3. Найти вероятность того, что с.в. Х примет значение, лежащее между

1 и 2

Решение:

1. Кривая распределения с.в. Х показана на рисунке.

2. По формуле для ф.р.:

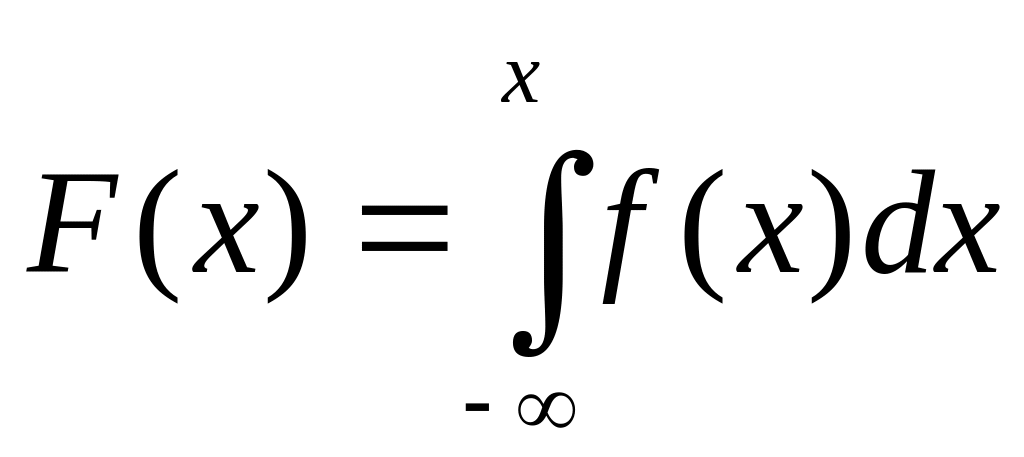
При х< 0 f(x)=0 

При х>0

 функция распределения:

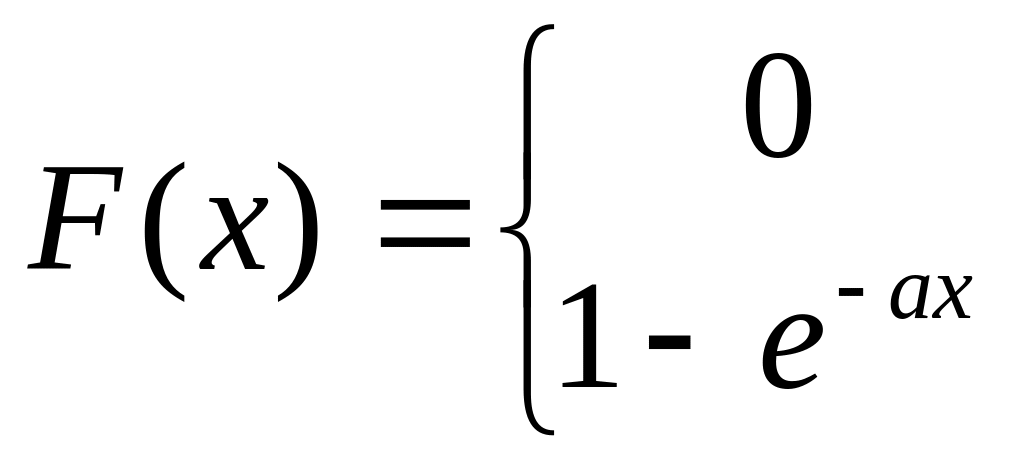
	при х<0
	при х>0

Г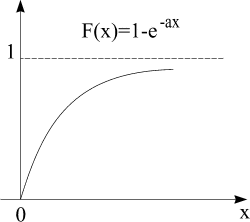 рафик функции:

3. Вероятность попадания с. в. Х на (1, 2).