2.6Формула полной вероятности.
Следствием общих основных правил теории вероятностей: правил сложения и умножения - является формула полной вероятности.
Теорема
Допустим, что существуют
- взаимоисключающие друг друга гипотезы
(предположения).
Пусть известны их вероятности:
Рассматривается некоторое событие А,
которое может появиться только вместе
с одной из гипотез
.
Известны
Требуется найти вероятность события
А.
Вывод:
По правилу сложения вероятностей:
По правилу умножения:
Формула полной вероятности:
Т. е. безусловная вероятность события А в опыте с гипотетическими условиями вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе.
Пример:
Имеются три одинаковые на вид урны:
В первой находятся 2 белых и 3 чёрных шара, во второй - 4 белых и 1 чёрный и в третей - 3 белых шара. Человек произвольно подходит к одной из урн и вытаскивает один шар. Какова вероятность, что шар белый ?
Решение:
А - вытащили белый шар
- выбрана первая урна.
- выбрана вторая урна.
- выбрана третья урна.
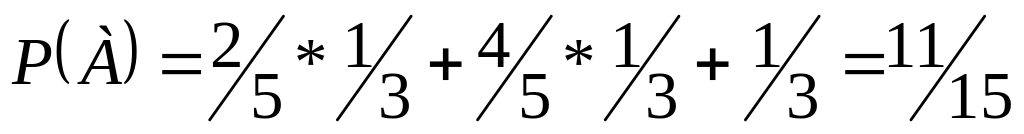
2.7Теорема гипотез (Формула Бейеса).
Теорема:
До опыта можно сделать n гипотез , таких что
(условие полной группы)
(условие несовместности)
Вероятность гипотез до опыта:
(априорные вероятности).
Опыт произведён. Произошло событие А.
Найти (апостериорные) вероятности
гипотез при условии, что опыт дал
результат А:
Формула Бейеса:
Возьмём любую
Из правила умножения вероятностей:
Делим на
,
получаем
Теперь подставим формулу полной вероятности для , получаем
Ввиду произвольности i эта формула подходит любой гипотезе.
Пример:
Имеется три урны: В первой - 3 белых и 1 чёрный, во второй - 2 белых и 3 чёрных и в третей - 3 белых. Человек произвольно подходит к одной из них и вынимает один шар. Шар оказался белым.
Найти после опытные (апостериорные) вероятности того, что шар вынут из 1 - й, 2 - й, 3 - й урны.
Решение:
А - вытащили белый шар.
- выбрана первая урна.
- выбрана вторая урна.
- выбрана третья урна.
Априорные вероятности:
Условные вероятности события А при гипотезах , , :
По формуле Бейеса:
Апостериорные вероятности гипотез:
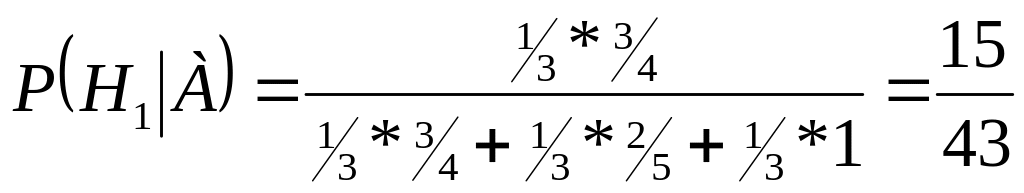
Таким образом в свете информации о появлении события А вероятности гипотез изменились: самой вероятной стала 3 - я гипотеза, наименее вероятной - 2 -я гипотеза.
Глава 3Случайные величины, их законы распределения.
3.1Понятие случайной величины. Законы распределения. Ряд распределения дискретной случайной величины.
Опр. Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение.
Опр. Множеством возможных значений случайной величины - называется множество всевозможных значений, которые может принимать с. в. в результате опыта.
Обозначим: 
– случайная величина
– i - ое возможное
значение с. в.
Примеры:
1). количество очков при бросании игральной кости:
2). Количество студентов на паре
3). время работы отремонтированного станка:
Опр. Дискретная с. в. - это с. в. множество значений которой счётно.
В противном случае с. в. - не дискретная.
В примерах 1) и 2) из выше перечисленных с.в.– дискретны, а пример 3) - с.в.– непрерывна.
Опр. Законом распределения с. в. - называется любое правило (таблица, функция) позволяющее находить вероятности всевозможных событий, связанных со с. в.
Опр. Рядом распределения с. в.
называется таблица. в верхней строке
которой перечислены в порядке возрастания
всевозможные значения с. в.
:
,
а в нижней - вероятности этих значений:
,
где
Замечание:
Ряд распределения является законом распределения, т.к. в его таблице уже содержатся вероятности событий связанных с ему соответствующей с.в.
Пример:
Рассматривается работа трёх независимо работающих тех. устройства (ТУ); вероятность того, что первое ТУ работает нормально - 0.2, второго - 0.4, третьего - 0.5.
С. в. Х - число работающих ТУ. Построить ряд распределения с. в. Х.
Решение:
Возможные значения с. в. Х: 0, 1, 2, 3.
Обозначим “ + “ - нормальная работа ТУ,
“ - “ - наоборот.
Геометрическая интерпретация.
Опр. Графическое изображение ряда распределения называется многоугольником распределения.
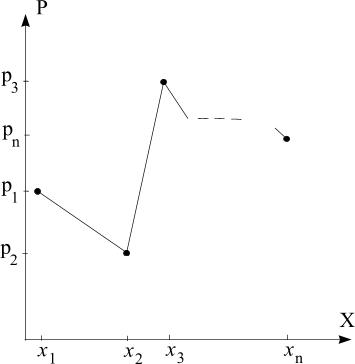
Рис. Многоугольник распределения