2.4Геометрическая модель.

Уже в самом начале развития теории вероятностей была замечена недостаточность “классической“ модели теории вероятности, основанной на рассмотрении конечной группы равновероятных событий. Уже тогда частные примеры привели к некоторому видоизменению этой модели и построению модели также для случаев, когда мыслимо бесконечное множество исходов. При этом по прежнему основную роль играло понятие “равновероятности“ некоторых событий.

Для геометрической модели ставится задача:

Пусть например, на плоскости имеется некоторая область G и в ней содержится другая область g. В область G бросается точка наудачу и спрашивается, чему равна вероятность того, что точка попадёт в область g.

Причём попадания в любые две точки принадлежащие G имеют одинаковые вероятности.

Таким образом, по определению, вероятность попадания в область g при бросании наудачу точки в область G равна отношению меры измерения G и g.

Пример 1:

На уроке физкультуры ученик сдаёт метание мяча. Нормы на «5» более 30 метров. Он может равновероятно кинуть на расстояние от 25 до 40 метров. Какова вероятность, что ученик получит оценку «5»?

Решение: Длина области G (всех возможных значений) 15 метров (от 25 до 40).

Длина области g (благоприятных исходов в G) 10 метров (от 30 до 40).

Вероятность

Пример 2:

Преподаватель может равновероятно прийти в течении 15 минут после звонка. Какова вероятность, что он опоздает не более чем на пять минут?

Решение: Отрезок времени области G (всех возможных значений) 15 минут.

Отрезок времени области g (благоприятных исходов в G) 5 минут.

Вероятность

Пример 3:

Преподаватель может равновероятно прийти в течении 15 минут после звонка. Какова вероятность, что он придет ровно в пять минут после звонка?

Решение: Отрезок времени области G (всех возможных значений) 15 минут.

Отрезок времени области g (благоприятных исходов в G) равен 0 (длина точки).

Вероятность

Пример 4:

Два лица А и В условились встретиться в определённом месте между 12 часами и одним часом дня. Пришедший первым ждёт в течении 20 минут, после чего уходит.

Чему равна вероятность встречи этих двух лиц, если приход каждого из них в течении указанного часа может произойти наудачу и моменты их прихода независимы.

Р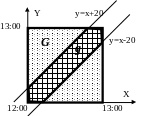 ешение:

Пусть Х - момент прихода лица А.

Y - лица В.

Условие встречи:

Примечание: Необходимо обратить внимание, что измерение областей всех возможных значений (G) и в ней области благоприятных исходов (g) может быть какой угодно, и в любых единицах измерения. Всё зависит от постановки задачи, как хорошо видно в примерах 1,2,4.

2.5Условная вероятность события. Правило умножения вероятностей.

Опр. Пусть в опыте существуют события А и В.

Условной вероятностью события В при наличии события А называется величина

Пример задачи:

Найти вероятность социолога среди женщин.

Т.е. необходимо найти «условную вероятность того, что случайно выбранное лицо социолог, при условии что оно является женщиной», т. е. мы рассматриваем только женщин и находим вероятность нахождения среди них социологов.

Правило умножения вероятностей: (теорема)

Вероятность произведения (пересечения) двух событий равна произведению вероятности одного из них на условную вероятность другого при наличии первого.

Пример: Из урны с 4 белыми и 3 чёрными шарами вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

Решение: С - оба шара – белые.

или

где А - первый шар белый

В - второй шар белый

очевидно

Теперь если событие А свершилось то осталось 6 шаров и среди них 3 белых, следует

следует

Другой путь:

Всего: (нет важности в порядке вытащенных шаров)

Благоприятных случаев - если первые два шара с 1 по 4,

т. е. причём при каждом из них можно составить (7 - 2) ! перестановок т.е.:

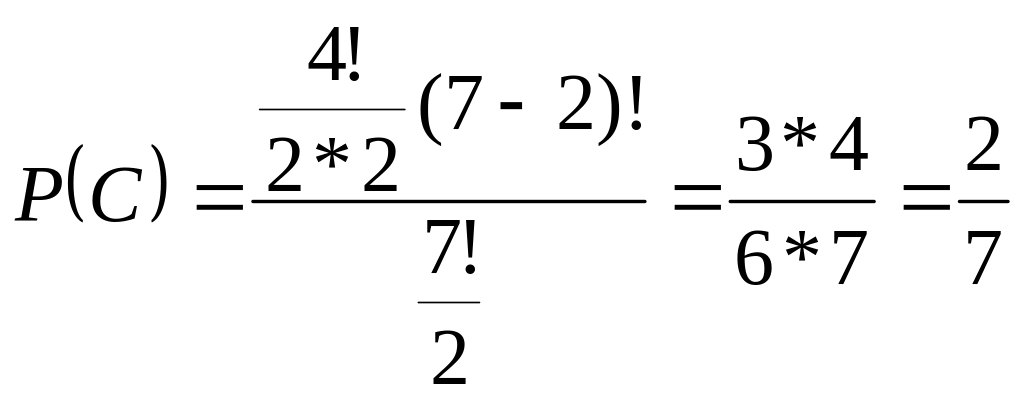
Правило умножения вероятностей для произвольного числа случаев:

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причём вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.

Опр. Событие а называется независимым от события В, если его вероятность не зависит от того, произошло В или нет, т.е.

В противном случае если событие А зависит от В.

Теорема:

Зависимость и независимость событий всегда зависимы.

Другая формулировка теоремы:

Если событие А зависит от В, то и В зависит от А.

И наоборот если А не зависит от В. то и В не зависит от А.

Доказательство:

Пусть

И наоборот

Опр. Два события называются независимыми, если появление одного из них не меняет вероятности появления другого.

Правило умножения для независимых событий:

т. е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Опр. Несколько событий называются независимыми, если любое из них не зависит от любой комбинации (произведения) любого числа других.

Замечание: Попарная независимость ещё не означает их независимость в совокупности.

P. S. В природе нет абсолютно независимых событий.

Пример применения правил теории вероятностей:

Имеется две урны, в первой 2 белых и 3 чёрных шара, во второй - 4 белых и 2 чёрных шара. Из каждой урны вынимается по одному шару. Найти вероятность того, что оба шара будут одного и того же цвета.

Решение:

Пусть А - оба шара одного цвета.

- белого - чёрного

- первый шар белый - первый шар чёрный

- второй шар белый - второй шар чёрный