1.3Частота или статическая вероятность.

Если производится серия из n опытов, в каждом из которых может появиться или не появиться событие А, то частота события А в данной серии называется количество опытов, в которых появилось событие А, а статистическая вероятность – это отношение числа опытов, в которых появилось событие А, к общему числу n произведённых опытов.

Обозначим - статистическую вероятность события А.

,

где

- число опытов, в которых событие А случилось (частота)

- общее число опытов.

С увеличением числа опытов статистическая вероятность приближается к некоторому числу (не сходится, стремится). Это число и можно назвать вероятностью события.

Правило сложения частот:

Если А и В несовместимы, то

Правило умножения частот:

Для любых событий A и В:

Понятие частоты события является кардинально важным в теории вероятностей. Можно построить всё её здание, исходя из основного понятия частоты и постулируя свойства не вероятностей, а частот (такое построение теории вероятностей было предложено ещё в начале XX века Р. Мизесом, да и в настоящее время многие авторы предпочитают излагать теорию вероятностей на частотной основе). Но более современной и более распространённой является аксиоматический теоретико-множественный подход, связанный с идеями А. Н. Колмогоровым, Этого подхода мы будем придерживаться в дальнейшем.

Глава 2Аксиоматика теории вероятности. Правила умножения и сложения и их свойства.

2.1Элементарные сведения из теории множеств.

Опр. Множеством называется любая совокупность объектов произвольной идентичной природы, каждый из которых называется элементом множества.

Пример: 1) Множество студентов института.

2. Множество чисел натуральных.

3. Множество точек (геометрия) на отрезке.

Опр. По числу элементов множества делятся на конечные и бесконечные.

Опр. Счётным множеством называется множество, в котором каждому элементу можно приставить индекс.

Пример:

Опр. Два множества А и В совпадают (или равны), если они состоят из одних и тех же элементов.

Обозначение: А=В

Опр. Объединением (суммой) множеств А и В называется множество С, состоящее из всех элементов множеств А и В и только их.

Обозначение:

Очевидно если и наоборот.

О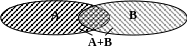 пр. Пересечением (произведением) множеств А и В называется множество D, состоящее из элементов принадлежащих и множеству А и множеству В одновременно.

Обозначение:

Очевидно если и наоборот.

Введём обозначения:

Ω – всё пространство (включает все элементы определённой природы)

Ø – пустое множество (не имеет ни одного элемента)

О пр. Противоположным множеству А называется множество , состоящее из всех элементов не принадлежащих множеству А.

Примечание: Данные определения имеют математический характер и удобны при решении задач, далее будут приведены определения суммы, произведения и противоположного событий на основе логики, предназначенные для описания реальных событий.

Свойства операций объединения и пересечения:

1). Переместительное свойство:

2). Сочетательное свойство:

3). Распределительное свойство:

Примечание (читателю рекомендуется самому вывести формулы исходя из определения):

A + A = A A A = A

A + = Ω A = Ø

Ω + A = Ω Ω A = A

Ø + A = A Ø A = Ø