12.3 Поле корреляции.
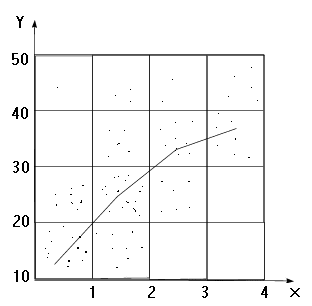
Пару случайных чисел можно изобразить в виде точки с координатами (х, у).
Задача упрощается, если выборку упорядочить.
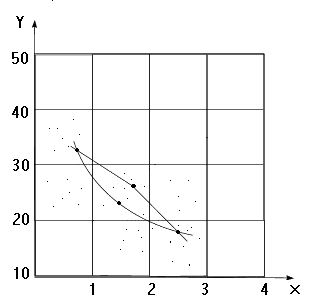
Опр. Если мы разобьём значения х и у на интервалы, затем нанесём координатную сетку, каждую пару значений переменных из данной выборки изображаем в виде точки, попавшей в определённую клетку, а далее мы рассматриваем эти клетки как элементы с количеством попаданий в них, то такое изображение корреляционной зависимости называется полем корреляции.
Опр. Если вычислить средние значения
у в каждом интервале изменения х
,
нанести эти точки на график и соединить
их между собой, то получим ломанную, по
виду которой можно судить как в среднем
меняется у в зависимости от изменения
х – такая ломанная линия называется
эмпирической линией регрессией.
-
0-1
1-2
2-3
3-4
my
10-20
20-30
30-40
40-50
mx
Опр. По выборочным данным можно построить таблицу, которая называется корреляционной таблицей.
12.4Линейная регрессия. Понятие о способе наименьших квадратов.
Линейная функция:
где а0 и а1 – коэффициенты регрессии.
а0 и а1 определяются по способу наименьших квадратов.
Метод наименьших квадратов:
хi – измеренное значение случ. величины.
- теоретическое значение случ. величины.
В случае линейной регрессии за
принимается
,
т.е.
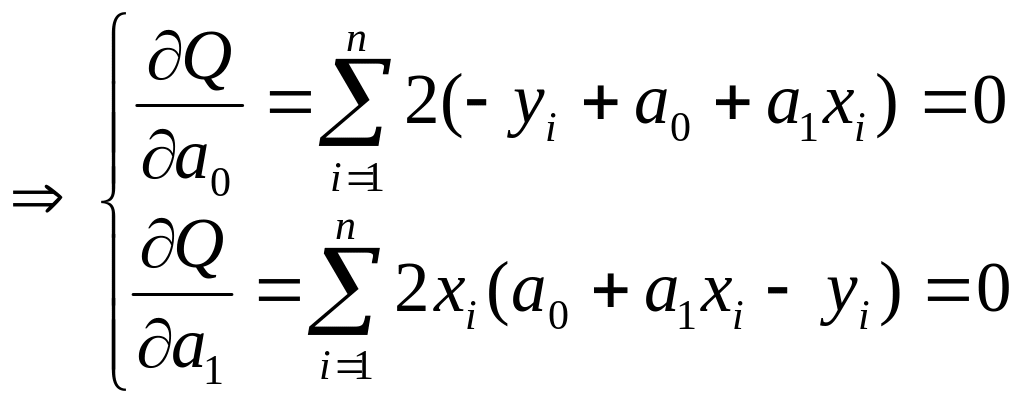
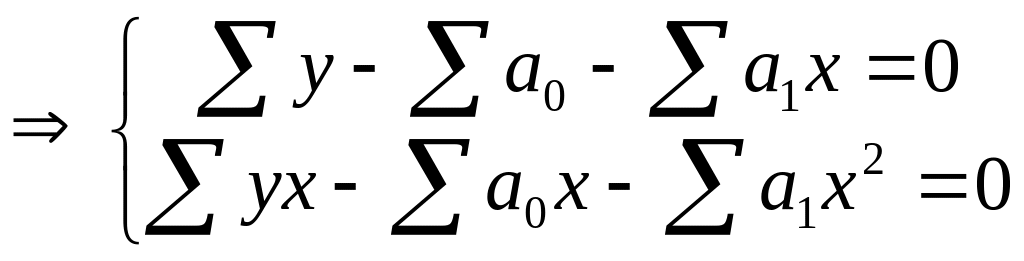- система нормальных уравнений
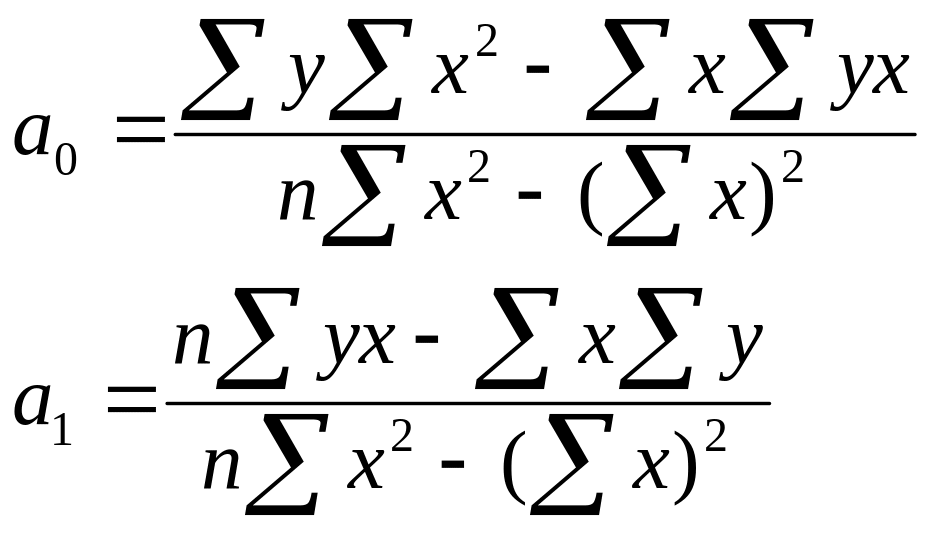
12.5Кривые регрессии. Нелинейная регрессия.
или
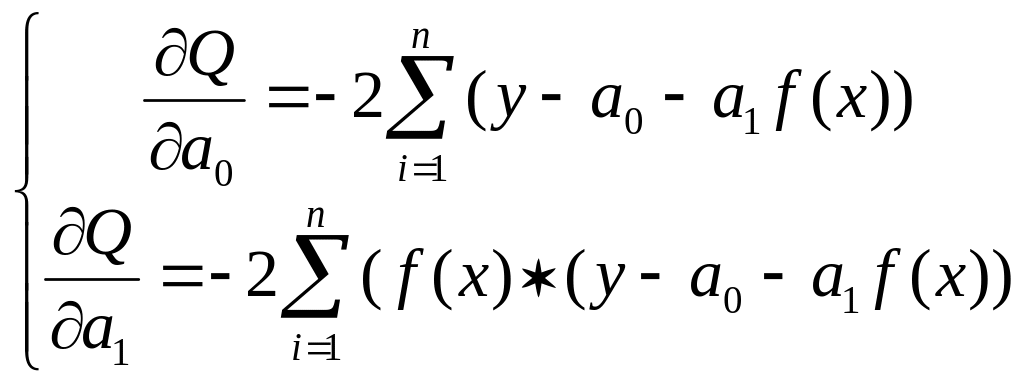
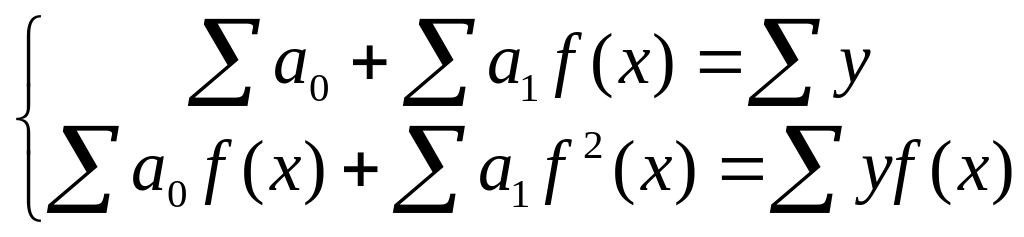
12.6Измерение тесноты связи. Эмпирическое корреляционное отношение.
а) б)
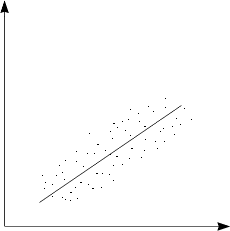
За основу берётся общий показатель изменчивости – полная дисперсия Y2.
Она раскладывается на две составляющие:
Обозначим:
-
это дисперсия переменной Y относительно
теоретической линии регрессии
.
Она измеряет влияние так называемых
прочих факторов на Y.
- это дисперсия теоретической линии
регрессии относительно условной
генеральной средней.
Она измеряет влияние Х на Y.
Доказательство:
Так как 1
//
Теоретическое корреляционное отношение:
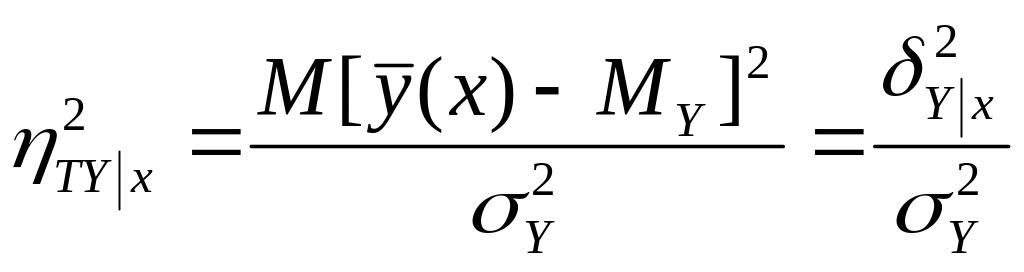
Если наличие связи ещё не определено и возможна ситуация её не существенности, то необходимо вычислить эмпирическое корреляционное отношение.
у- измеренное значение
-
среднее значение для интервала
k – общее число интервалов
n – количество измерений
-
дисперсия зависимой переменной у
относительно эмпирической линии
регрессии.
-
межгрупповая дисперсия (дисперсия
эмпирической линии регрессии относительно
средней всей совокупности)
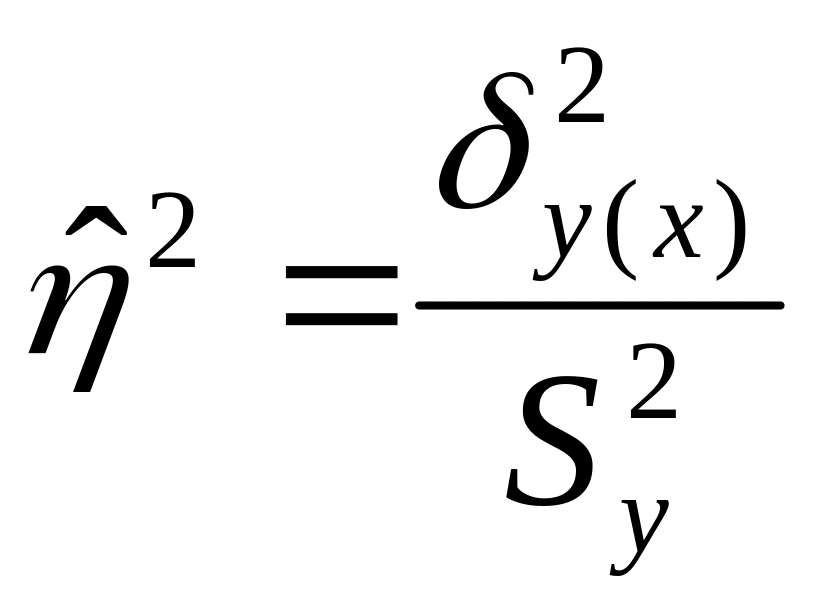- эмпирическое корреляционное
отношение.
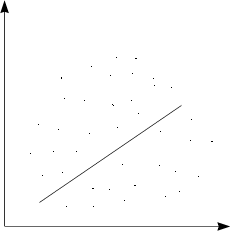
12.7Коэффициент корреляции.
Зависимость между Х и Y – линейна.
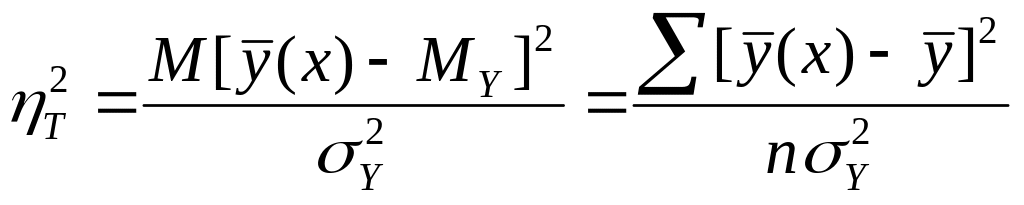
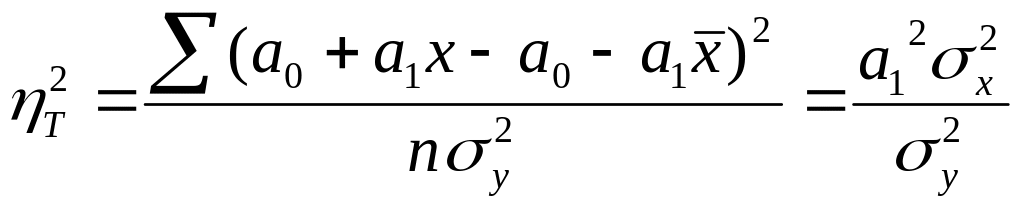
Заменим а12:
\\
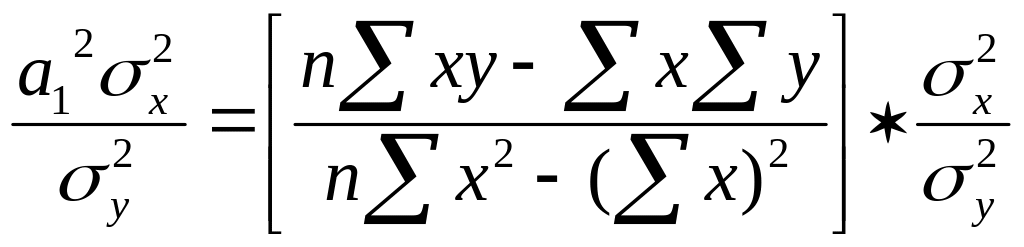
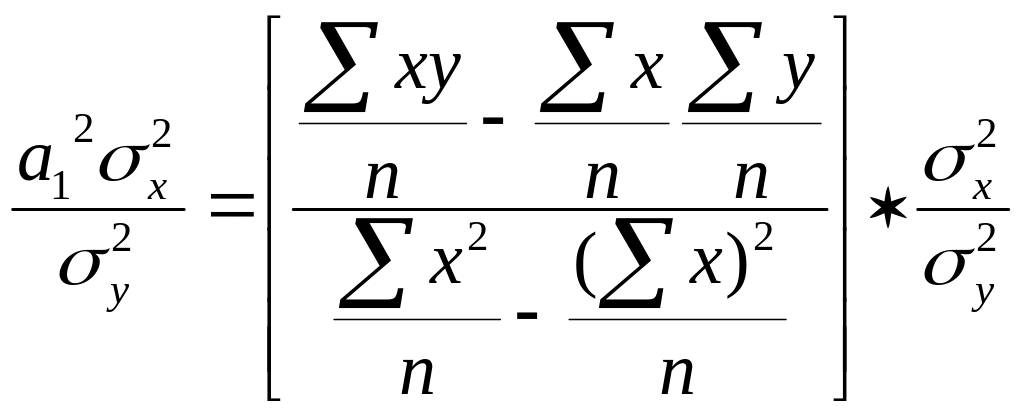
х2
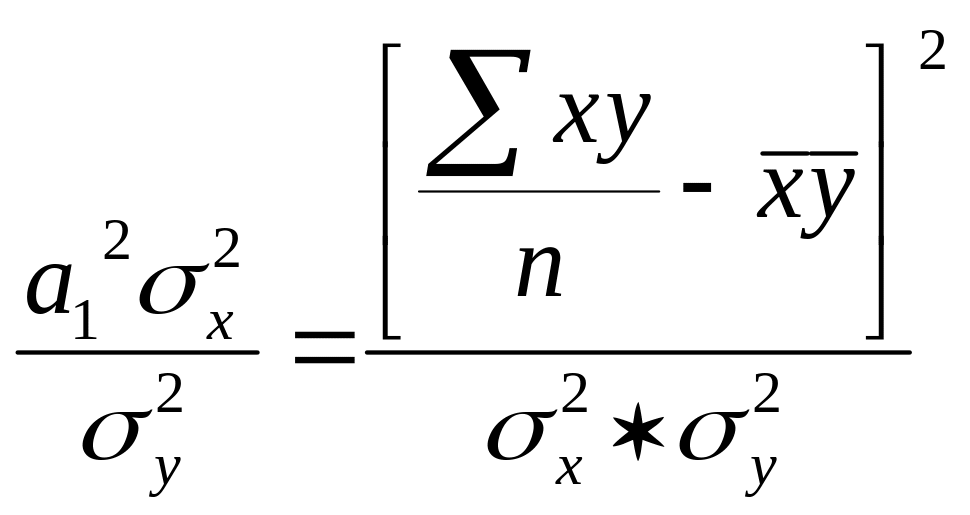
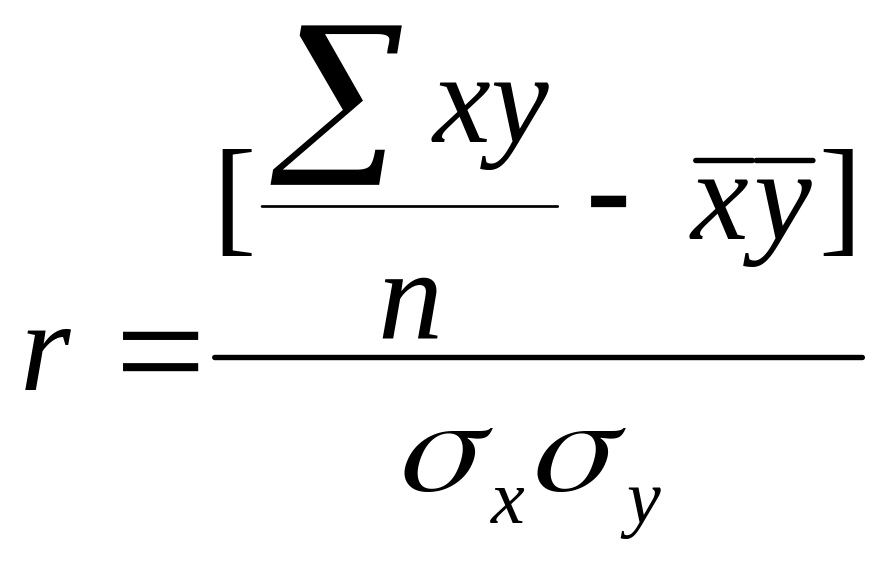- выборочный коэффициент корреляции
или
Теорема 5.1.
Коэффициент корреляции принимает значения в интервале от -1 до +1
Доказательство:
\\ \\
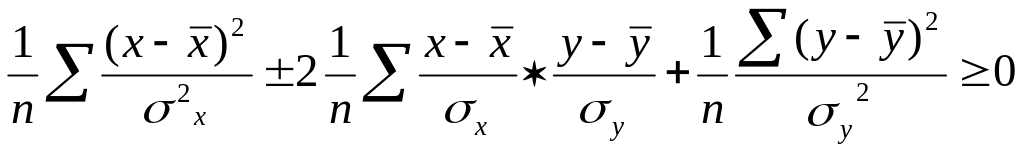
1 1
1 2r + 1 0 -1 r +1
12.8Интервальное оценивание коэффициента корреляции и коэффициентов регрессии.
Точечной оценкой коэффициента корреляции является эмпирический коэффициент корреляции r.
r лишь при очень близком к нормальному закону распределения является надёжной оценкой .
Нормальный закон распределения с (, r)
r – эмпирический коэффициент корреляции
tq – параметр нормированной функции Лапласа (находится в таблице по заданию доверительной вероятности)
12.9Множественная регрессия.
х1,х2,…,хn- несколько случайных величин
а1,а2,…,аn- коэффициенты регрессии
Опр. Метод, позволяющий по выборке, которая содержит отдельные наблюдавшиеся значения переменных у, х1,х2,…,хn оценить значение неизвестных параметров а1,а2,…,аn, называется множественной регрессией.
Коэффициенты регрессии находятся по признаку наименьших квадратов.
12.10Коэффициент корреляции рангов. Объединенные ранги.
Пусть n индивидуумов имеют по качеству А следующие ранги (места): Х1, Х2,…, Хn, а по В следующие: Y1, Y2,…, Yn.
Обозначим Хk-Yk=dk
d – характеризует тесноту связи
Если все d равны нулю, то соответствие полное.
Так как значения рангов Х расположены от 1 до n, их сумма:
Так же и для Y.
Обозначим через |
|
- отклонение от среднего |
|
|
Коэффициент корреляции рангов Спирмена:
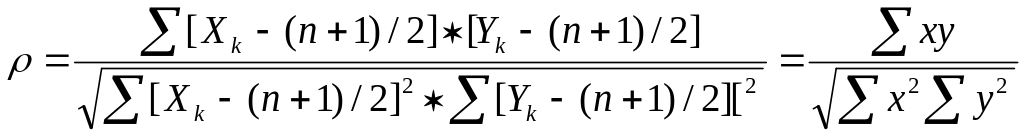
