11.3Двухфакторный комплекс.

Если исследуют действие двух, трех и т.д. факторов, то структура дисперсионного анализа та же, что и при однофакторном анализе, усложняются лишь вычисления.

Предположим, что имеется несколько однотипных станков и несколько видов сырья.

Требуется выяснить, значимо ли влияние различных станков и качества сырья в партиях на качество обрабатываемых деталей.

Факторы: А- влияние станков

В- влияние качества сырья в партиях

			…		…
			…		…
			…		…
…	…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…	…
			…		…
			…		…

- размер обрабатываемой детали

Пусть имеется r

v

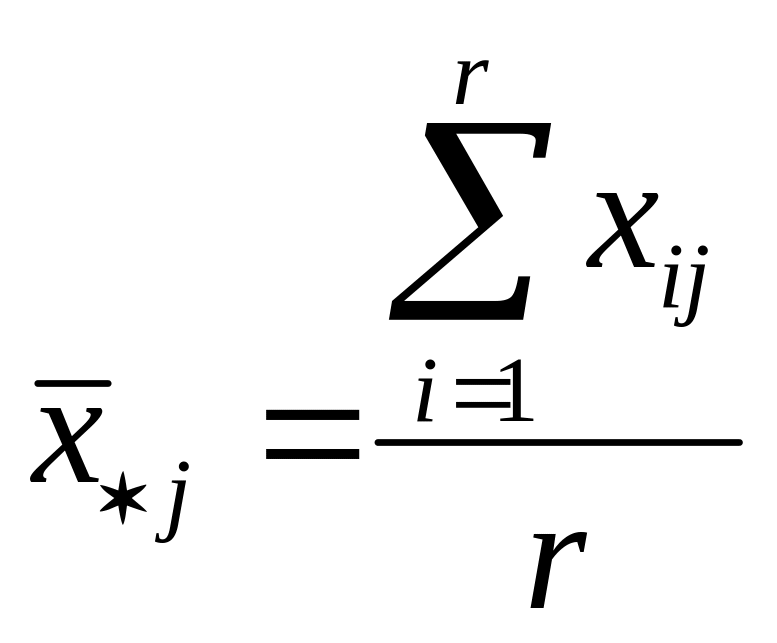
- характеризует изменение признака по фактору А

- характеризует изменение признака по фактору В

- остаточная сумма, характеризует влияние неучтенных факторов

Оценки дисперсий:

В двухфакторном анализе для выяснения значимости влияния факторов А и В на исследуемый признак сравнивают дисперсии по факторам с остаточной дисперсией, т.е оценивают отношения:

и

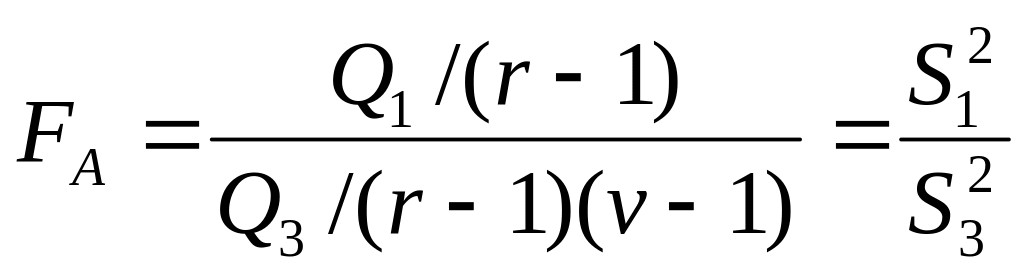
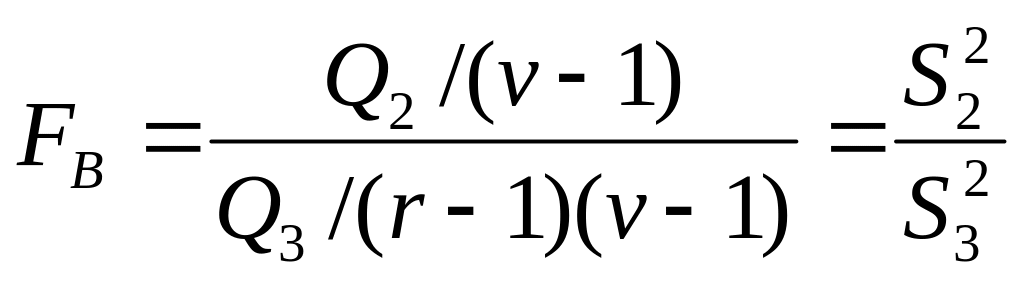
Полученные значения и сравнивают с табличными при выбранном уровне значимости .

При и - влияние факторов А и В незначительно.

Пример построения двухфакторного комплекса.

В

А
	1	2	3	2
	5	6	10	7
	3	4	6.5	4.5

+

Q=37,5+13+3=53,5

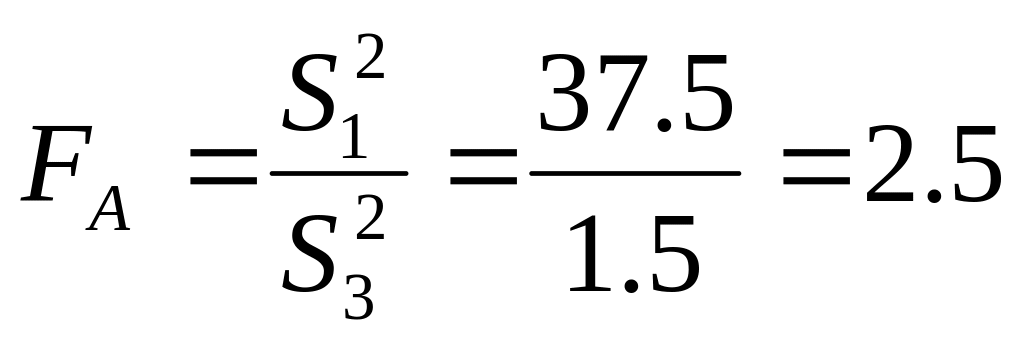
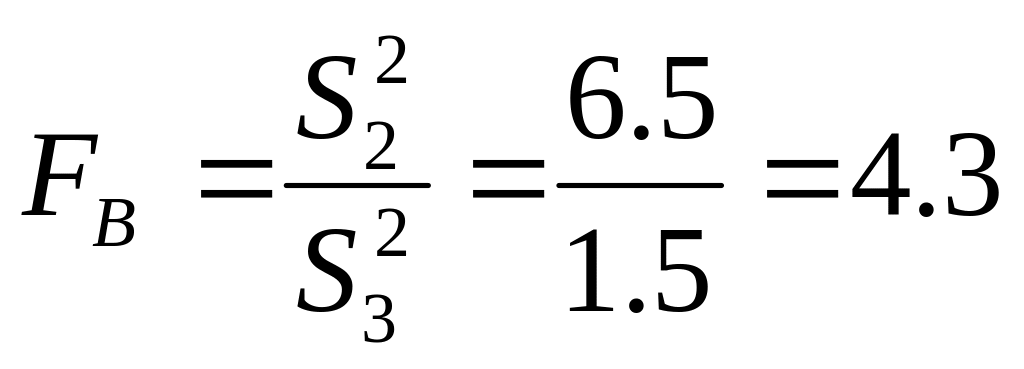
=0,05

>

<

Вывод: Влияние фактора А - значительно

Влияние фактора В - незначительно.

11.4Дисперсионный анализ с равным числом наблюдения в ячейке.

При одном измерении в ячейке схема проста, но достоверность выводов незначительна.

Рассмотрим схему двухфакторного дисперсионного анализа с равным числом наблюдений в каждой ячейке.

Опр. Пропорциональным называется такой комплекс, в котором количества наблюдений в ячейках любых двух строк или столбцов пропорциональны.

			…
	…	…	…	…
	…	…	…	…	…
…	…	…	…	…	…
	…	…	…	…	…
		…	…	…

- среднее значение в ячейке

- среднее значение по строке

- среднее значение по столбцу

- общее среднее

Теперь:

число степени с.в.

v-1 - по фактору А

r-1 - по фактору В

(v-1)(r-1) - взаимодействие

(k-1)rv - остаточная

rkv-1 - полная сумма

Пример построения двухфакторного комплекса с равным числом элементов в ячейке.

В текстильной промышленности важным является выявление факторов, влияющих на качество пряжи, с тем,чтобы в дальнейшем их можно было регулировать.

	B1					B2
А1	190	260	170	170	170		190	150	210	150	150
А2	150	250	220	140	180		230	190	200	190	200
А3	190	185	135	195	195		150	170	150	170	180

При каждом уровне наладки в каждой партии сырья находим средние:

	В1	В2
А1
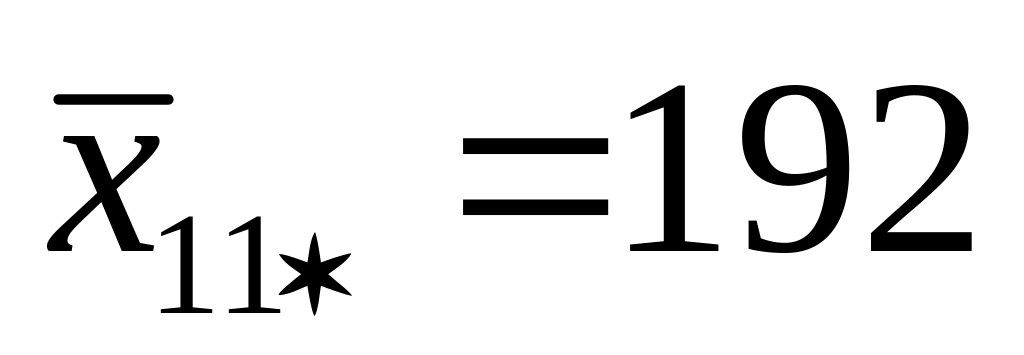
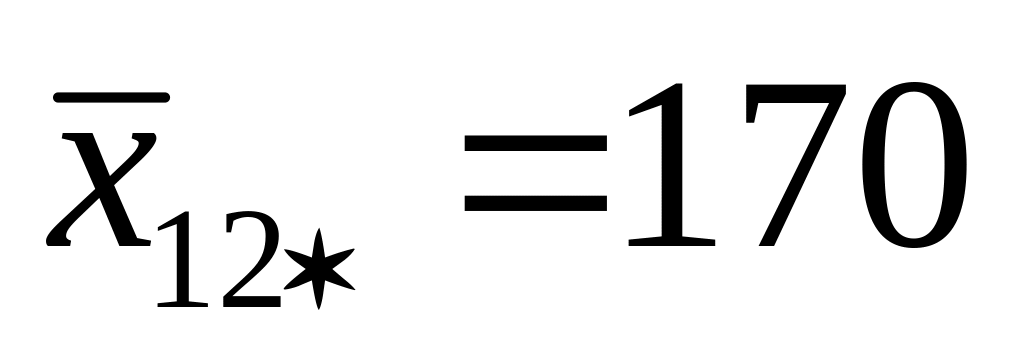
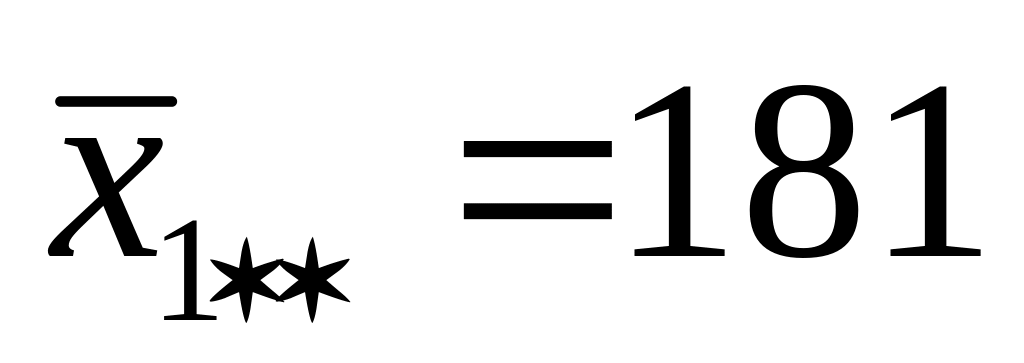
А2
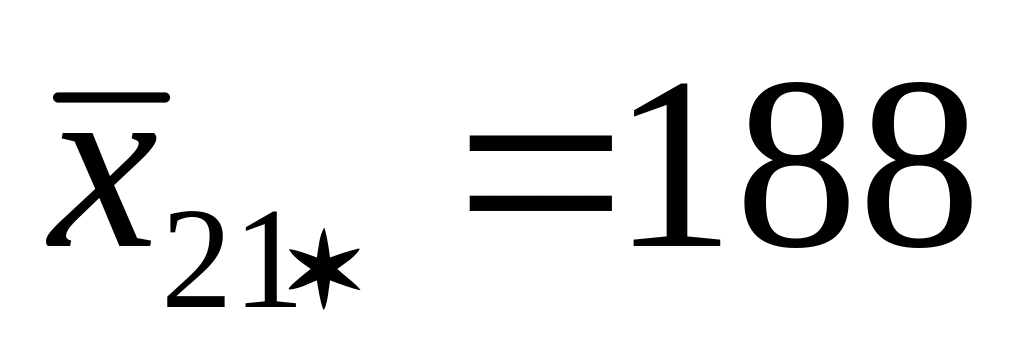
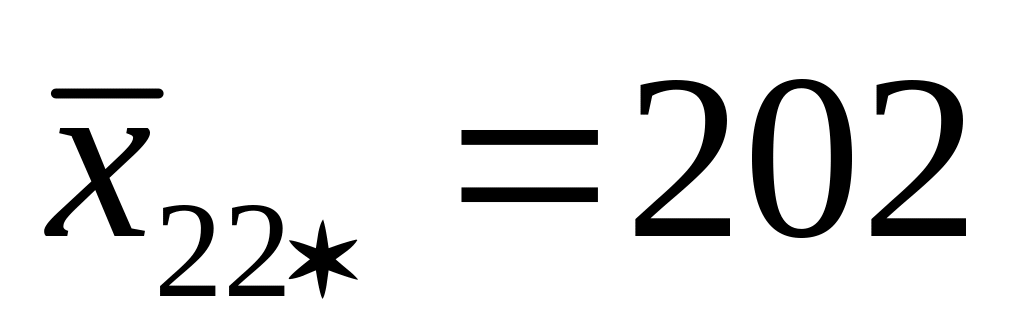
А3
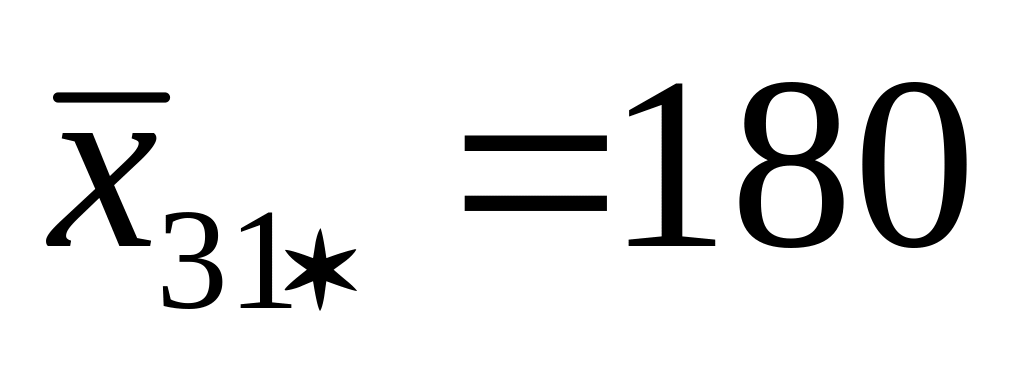
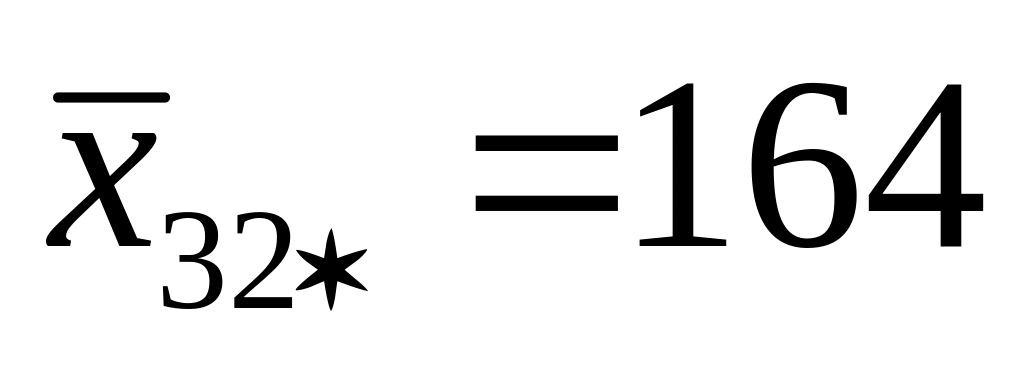
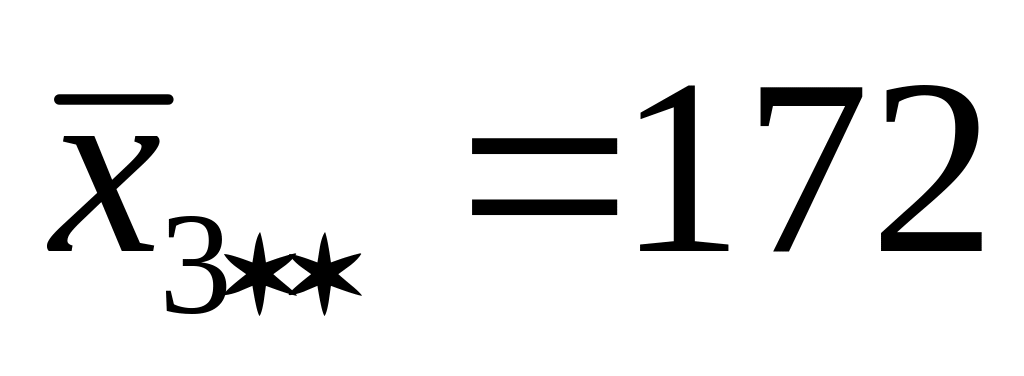
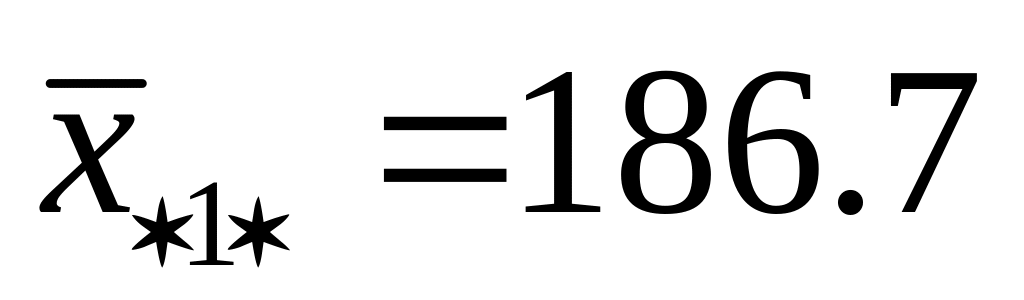
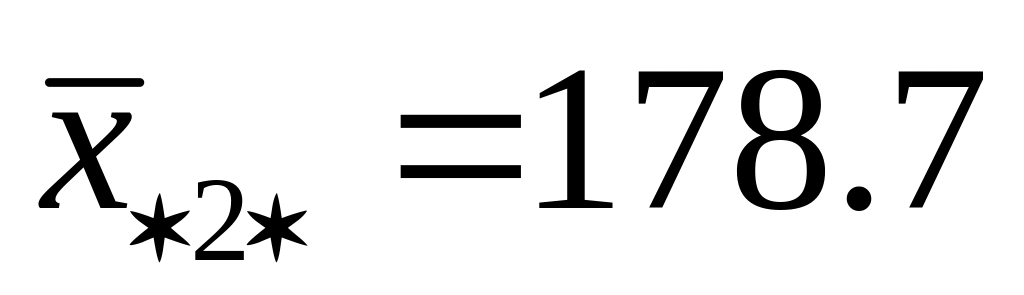
			182,7

Находим сумму квадратов:

Q₁=2686,6

Q₂=480

Q₃=1860

Q₄=22360

Q=2686,7+480+1860+22360=27386,7

Вычисляем оценки дисперсий:

Число степеней свободы:

1

2

2

24. 

29. 

Вычисляем отношения дисперсий:

При уровне значимости =0,05 k₄=24, k₁=1  F_А=4,26

k₄=24, k₂=2  F_В=3,40

F_А< F_А и F_В< F_В

Следовательно, нулевая гипотеза о равенстве средних не отвергается, т.е. влияние фактора А (уровня наладки станков) и фактора В (партии сырья) на величину разрывной нагрузки незначительно.

В тех случаях, когда каждый последующий фактор сгруппирован внутри предыдущего, мы имеем дело с многофакторным комплексом.

Четырехфакторный комплекс.

Четыре типа изоляционного покрытия (фактор А)

Два уровня температуры (фактор В)

Два уровня давления (фактор С)

Четыре стальные панели, имеющие данное покрытие (фактор D)

Случай одного наблюдения в ячейке.

Фактор А		1				2				3				4
Фактор В		1		2		1		2		1		2		1		2
Фактор С		1	2	1	2	1	2	1	2	1	2	1	2	1	2	1	2
Фактор D	1	х1111	х1121						х2221								х4221
	2	х1112	х1122						х2222								х4222
	3	х1113	х1123						х2223								х4223
	4	х1114	х1124						х2224								х4224

Q=Q_A+Q_B+Q_C+Q_D+Q_AB+Q_AC+Q_AD+Q_BC+Q_BD+Q_CD+Q_ABC+Q_ABD+Q_ACD+Q_BCD+ +Q_ABCD