10.6Вычисление объёма выборки.

После того как для оценки интересующего параметра генеральной совокупности обоснованно выбран способ образования выборки, приступают к расчету необходимого объёма выборки, задавшись желаемой степенью точности оценки и доверительной вероятностью .

Рассмотрим случайную выборку с возвратом:

Х – нормально распределена

- известна

Интервал мат. ожидания:

Длина доверительного интервала:

Длина доверительного интервала определяет точность параметра

откуда

Если неизвестна, то предварительно берут небольшую пробную выборку и по её данным делают приближенную оценку параметра .

где - выборочная дисперсия пробной выборки

- число, взятое из таблицы, соответствующее вероятности p и числу наблюдений n.

Глава 11Основы дисперсионного анализа.

11.1Основная идея дисперсионного анализа.

Опр. Дисперсионный анализ – это статистический метод анализа результатов наблюдений, зависящих от различных, одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния.

Основная идея дисперсионного анализа заключается в разложении общей дисперсии случайной величины на независимые случайные слагаемые, каждое из которых характеризует влияние того или иного фактора, или их воздействие.

Последующее их сравнение позволяет оценить существенность влияния факторов на исследуемую случайную величину.

Пусть Х исследуемая сл. величина,

А и В - влияющие на неё факторы

Допустим

где - среднее значение Х

- отклонение, вызываемое фактором А

- отклонение, вызываемое фактором В

- отклонение, вызываемое другими факторами

Пусть также , , - независимые сл. величины

- дисперсии соответствующих Х, , и 

Сравнивая и мы можем сравнить влияние факторов А и В

А рассмотрев можно установить степень влияния факторов А и В на величину Х.

Опр. Если исследуется влияние одного фактора на исследуемую величину, то речь идет об однофакторной классификации или однофакторном комплексе.

Опр. Если изучается влияние двух факторов, то речь идет о двухфакторном комплексе.

11.2Однофакторный комплекс.

Пример: производятся детали одного типа на параллельно работающих станках.

Определяется насколько однотипны средние размеры выпускаемых деталей.

Здесь имеет место лишь один фактор, влияющий на размеры деталей, - станки на которых они изготавливаются.

Для решения этой задачи сравниваются средние по каждому станку размеры деталей между собой и оценки существенности разницы этих средних.

Пусть совокупности размеров имеют нормальное распределение.

Имеется m таких совокупностей.

Их объёмы

Х _i - ая совокупность

Т

Количество элементов в совокупности

огда все выборки можно записать в виде следующей таблицы, которая называется матрицей наблюдений.

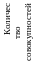
	1	2	…	i	…	n
1			…		…
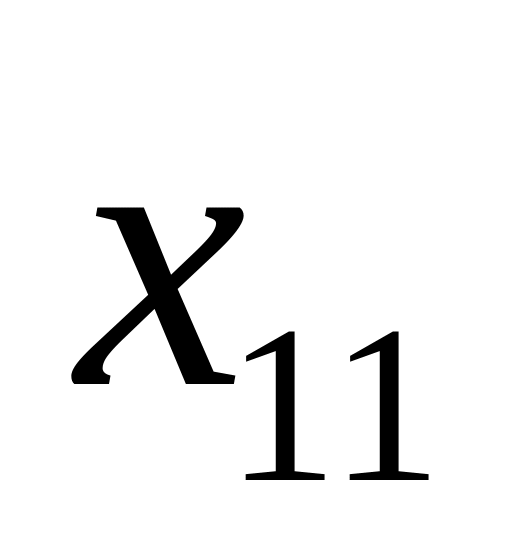
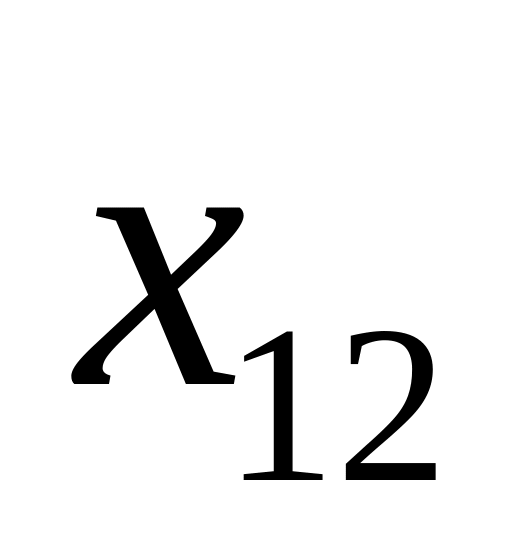
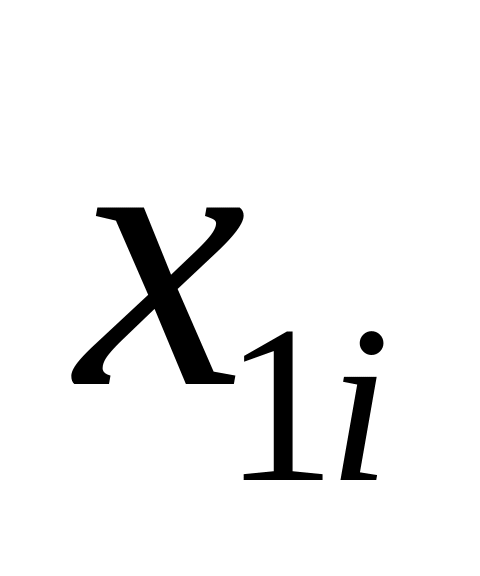
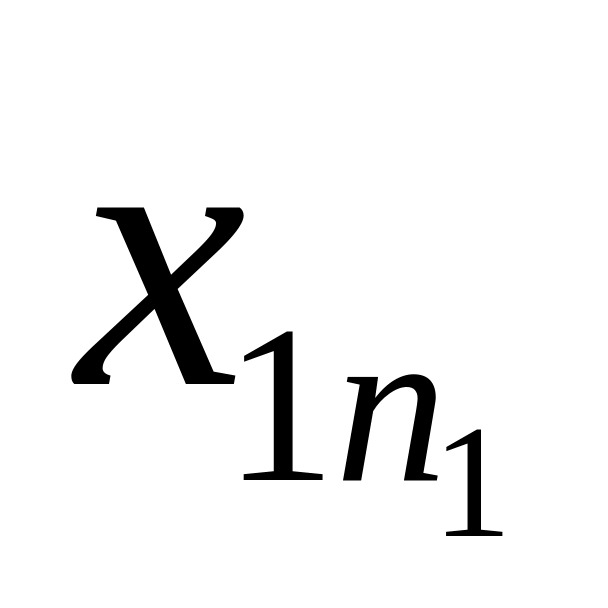
2			…		…
…	…	…	…	…	…	…
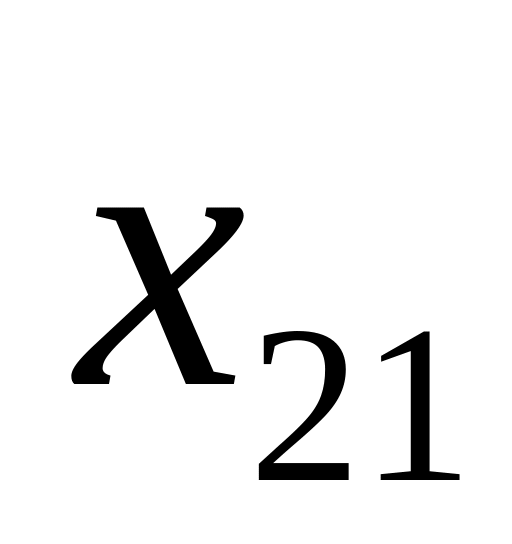
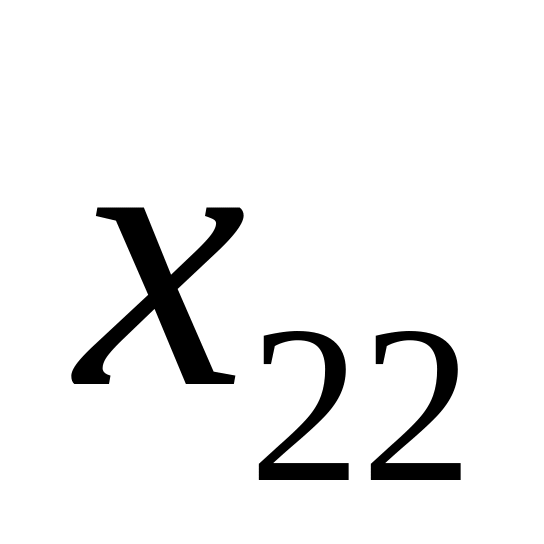
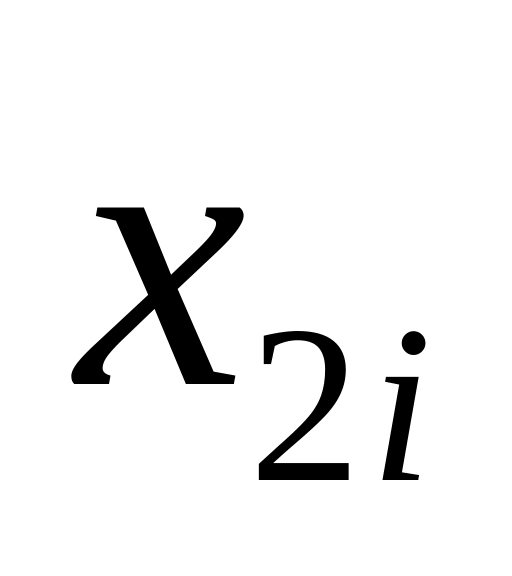
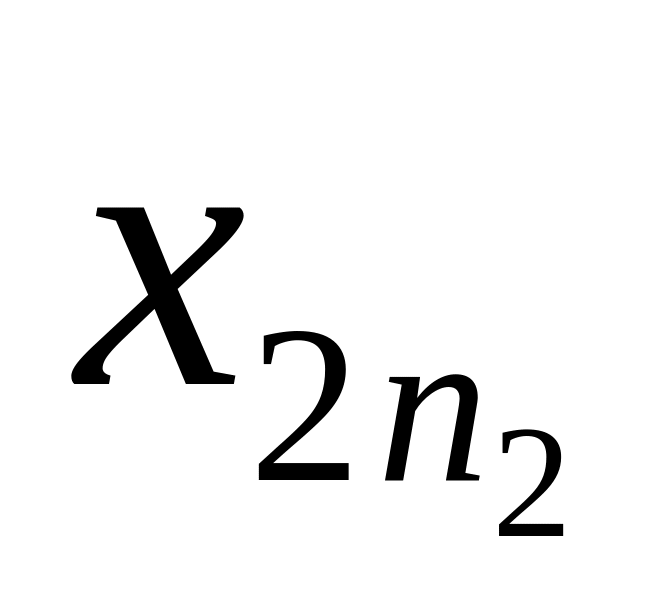
m			…		…

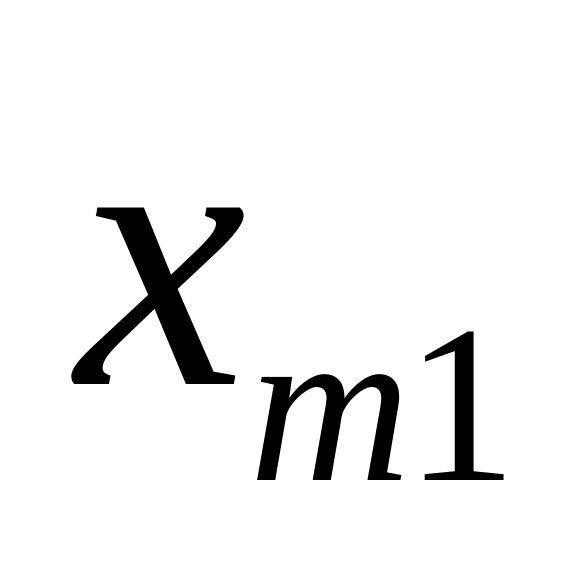
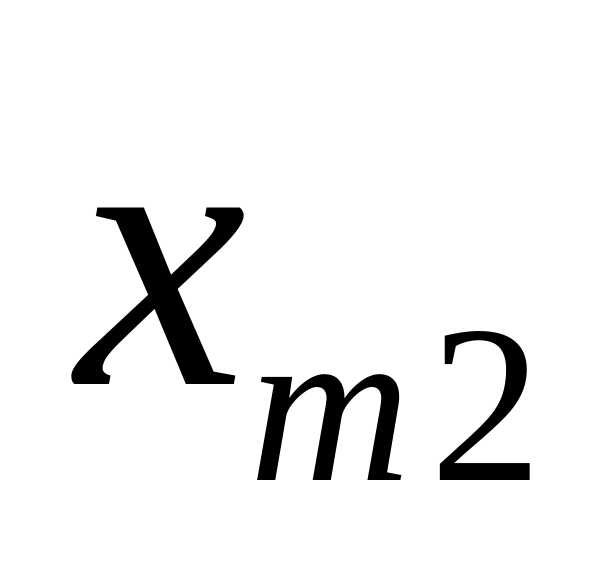
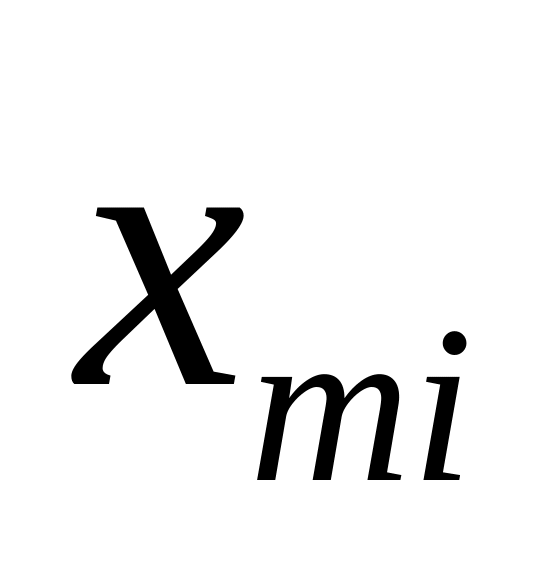
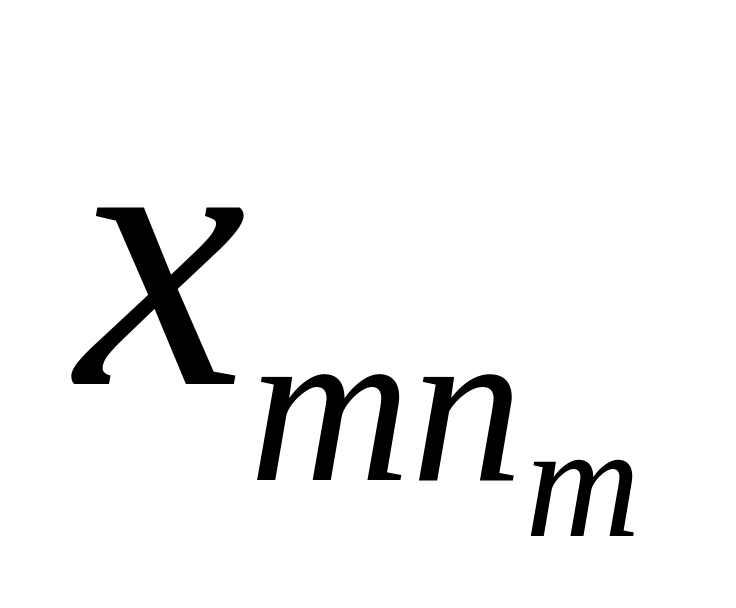
- средние выборок

Сделаем гипотезы:

:

:

Средние по совокупностям:

; ;

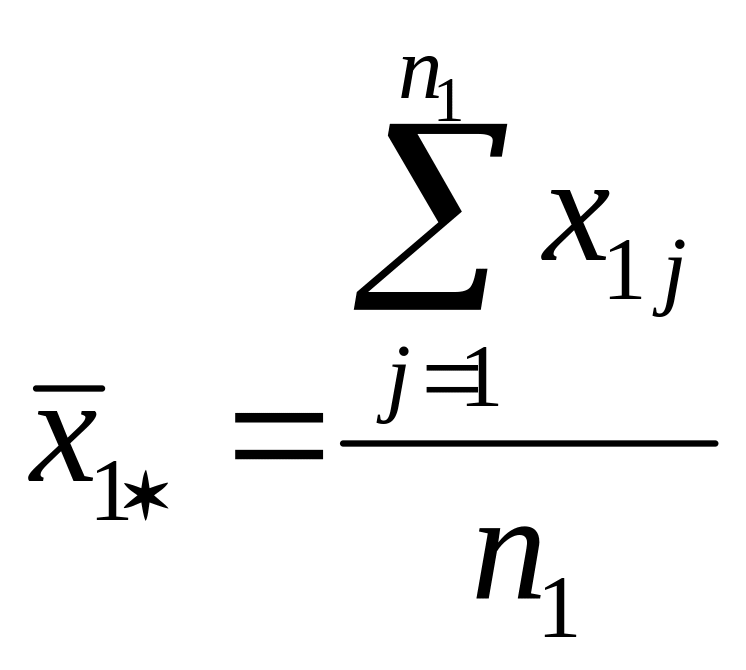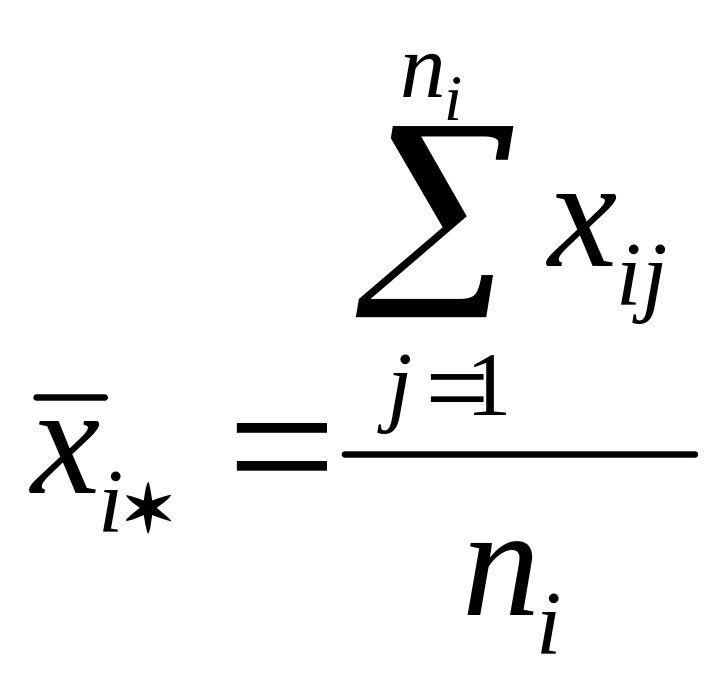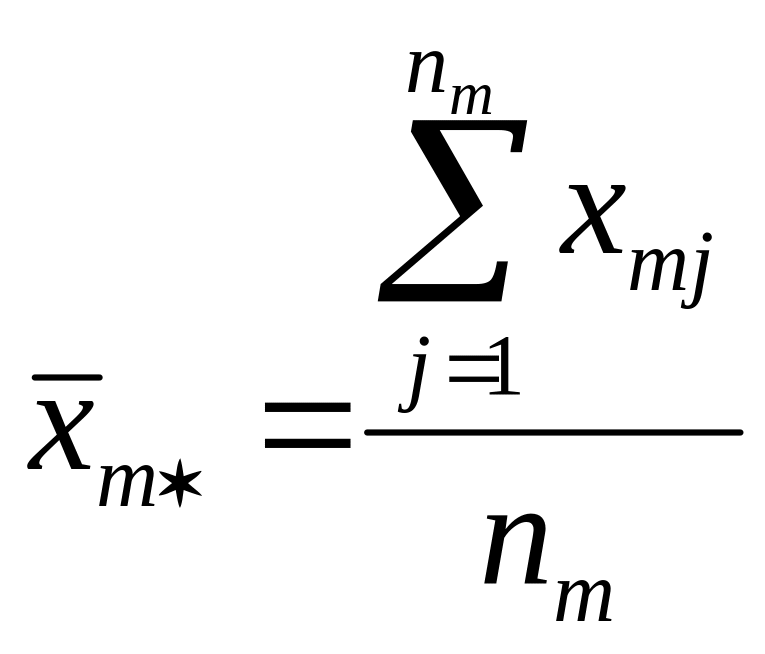
Общая средняя:

Сумма квадратов отклонения:

Причем S=



\\ \\

Q1 Q2

Опр. Q - эта сумма называется суммой квадратов отклонений между группами и характеризует систематическое расхождение между совокупностями наблюдений.

Q1 называется рассеиванием по факторам (т.е. за счет используемого фактора)

Q2 представляет собой сумму квадратов разностей между отдельными наблюдениями и средней соответствующей совокупности.

Q2 называется суммой квадратов отклонений внутри группы.

Оценки дисперсий:

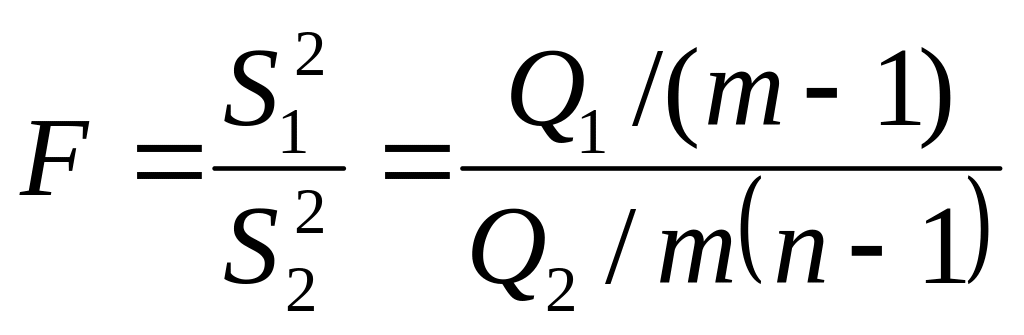
Этот критерий подчиняется F- распределению с и степенями свободы.

Выбирая уровень значимости , по таблице находим предел, так чтобы

По величине отношения межгрупповой и остаточной дисперсии судят насколько сильно проявляется влияние факторов.

Пример построения однофакторного комплекса.

Имеем четыре партии сырья для текстильной промышленности.Из каждой партии отобрано по пять образцов и произведены испытания на определение величины разрывной нагрузки.

№ партии	Р а з р ы в н а я н а г р у з к а
1	200	140	170	145	165
2	190	150	210	150	150
3	230	190	200	190	200
4	150	170	150	170	180

Требуется выяснить, существенно ли влияние различных партий сырья на величину разрывной нагрузки.

Решение:

m=4 n=5

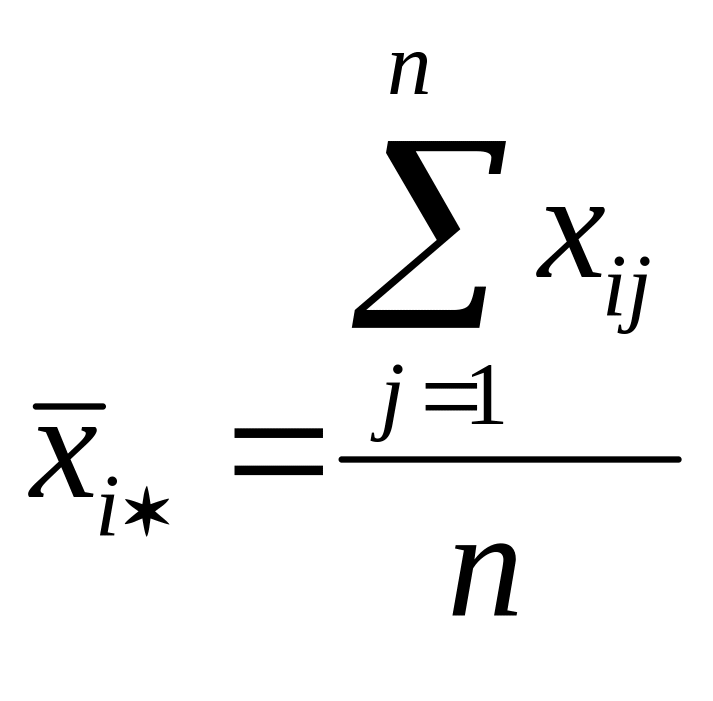
=164 =170 =202 =164

=700/4=175

При и =0,01

=9,01  >F

Вывод: различие между сырьем в партиях не влияет на величину разрывной нагрузки.