9.6Распределение дисперсии в выборках из нормальной генеральной совокупности. Распределение Пирсона.
Рассмотрим закон распределения выборочной дисперсии, рассчитанной для наблюдений, взятых из нормальной совокупности.
При анализе распределения дисперсии выборки следует иметь ввиду следующие два случая:
1) мат. ожидание случайной величины известно
2) мат. ожидание случайной величины неизвестно
Случай 1 - мат. ожидание случайной величины Х
Случайная величина Х подчиняется нормальному закону распределения
с параметрами
- ряд независимых наблюдений, каждое из которых подчиняется нормальному закону распределения с мат. ожиданием и дисперсией.
Тогда выборочная дисперсия вычисляется по формуле:
Введём
- подчиняется нормальному закону с
и
Т.к. - независимы
также независимы
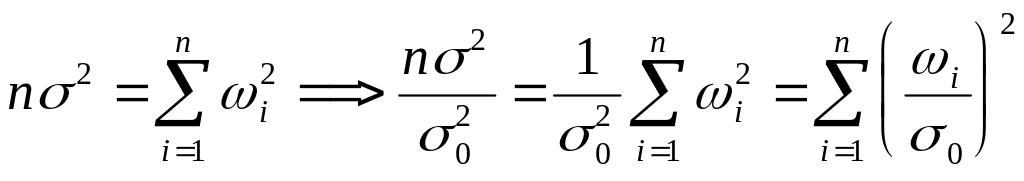
Пусть
,
u - подчиняется нормальному закону с
и
-
независимы
Обозначим
Опр. Случайная величина, представляющая
собой сумму квадратов n независимых
случайных величин
,
каждая из которых подчиняется нормальному
закону распределения с параметрами
называется случайной величиной с
распределением
и k=n степенями свободы.
Примечание: Число степеней свободы вычисляется по числу независимых переменных за вычетом количества связей, накладываемых на них.
L(n) - коэффициент, зависящий от объёма выборки
- текущая переменная
n - количество элементов в выборке
Замечание Распределение статистики не зависит ни от мат. ожидания, ни от дисперсии, а зависит лишь от объёма выборки.
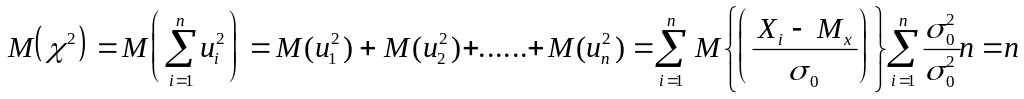
Замечание Следовательно, мат. ожидание равно числу степеней свободы.
(дисперсию
выводится в литературе).
Случай 2 Х - подчиняется нормальному закону распределения с параметрами
- ряд независимых наблюдений над случайной величиной Х.
Дисперсия выборки вычисляется по формуле:
Аналогично доказывается, что случайная
величина
имеет распределение
,
но с k=(n-1) степенями свободы.
9.7Понятие доверительного интервала. Доверительная вероятность.
В 2.3 были рассмотрены некоторые выборочные характеристики, которые лучше всего в смысле несмещенности, эффективности и состоятельности оценивали параметры распределения генеральной совокупности.
Опр. Оценка неизвестного параметра генеральной совокупности одним числом называется точечной оценкой.
Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания.
Опр. Доверительным интервалом
для параметра
называется такой интервал, относительно
которого можно с заранее выбранной
вероятностью
,
близкой к единице,утверждать, что он
содержит неизвестное значение параметра
,
т.е.
Вероятность принято называть доверительной вероятностью.
Замечание: Выбор доверительной вероятности не является математической задачей, а определяется условиями конкретно решаемой задачи.
9.8 Построение доверительного интервала для математического ожидания при известной .
Случайная величина Х распределена нормально
- известно
Требуется оценить неизвестное
Наилучшей оценкой для этого является выборочная средняя
нормированное отклонение
распределено нормально с M[
]=0
и
Вероятность любого отклонения
может быть вычислено по формуле
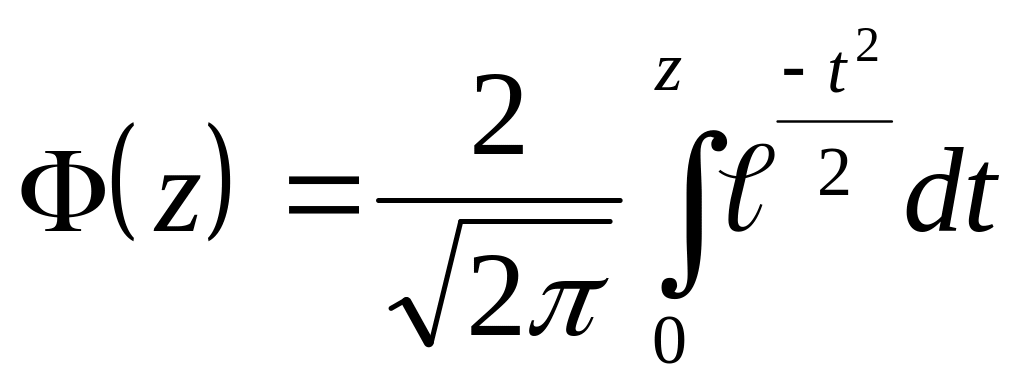табличный интеграл
Далее преобразовываем формулу:
( известно, требуется оценить неизвестное )
Перепишем в виде
Вывод: С вероятностью Ф(z) интервал
является доверительным интервалом для оценки .