9.2Основные свойства оценок.

1) Несмещенность

2) Эффективность

3) Состоятельность

Опр. Оценка параметра называется несмещенной, если её математическое ожидание равно оцениваемому параметру , т. е.

Если это равенство не выполняется, то возникает систематическая ошибка в оценке параметра .

Если - завышение значения

- занижение значения

Мера рассеивания около мат. ожидания характеризуется дисперсией .

Если , то в качестве оценки принимают .

Опр. Несмещенная оценка , которая имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра , вычисленных по выборкам одного и того же объёма, называется эффективной оценкой.

Опр. Оценка параметра называется состоятельной, если она подчиняется закону больших чисел, т.е. выполняется следующее равенство:

9.3Оценка математического ожидания и дисперсии по выборке.

Теорема 2.1 Арифметическая средняя , вычисленная по независимым наблюдениями над случайной величиной X, которая имеет мат. ожидание , является несмещенной оценкой этого параметра.

Док-во:

-независимые набл. над случ. величиной Х

, ,.....,

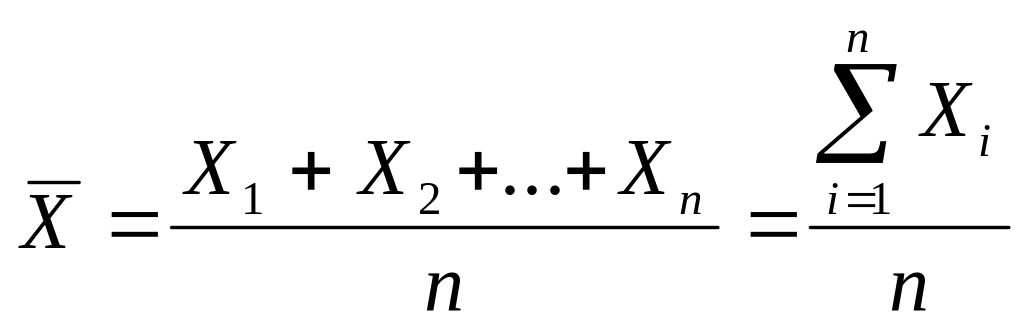
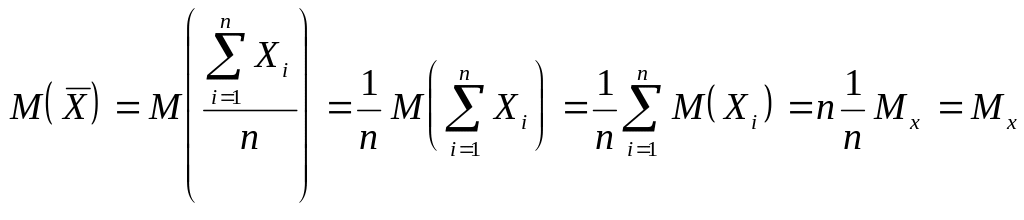
Теорема 2.2 Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной X, которая имеет математическое ожидание и дисперсию, является состоятельной оценкой этого параметра.

Док-во:

-независимые набл. над случ. величиной Х

Неравенство Чебышева:

, ,....,

Теорема 2.3 Если случайная выборка состоит из n независимых наблюдений над случайной величиной Х с математическим ожиданием и дисперсией, то выборочная дисперсия 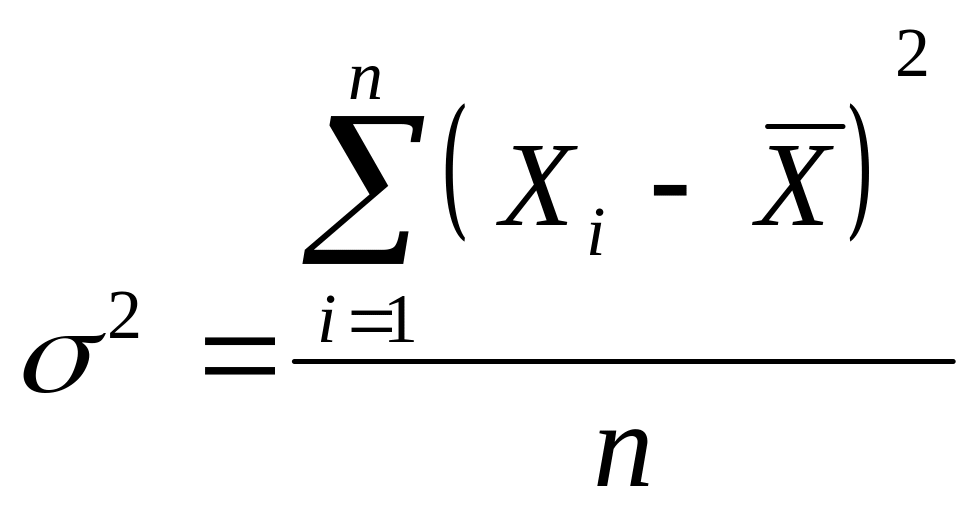, не является несмещенной оценкой генеральной дисперсии.

Док-во:

-независимые набл. над случ. величиной Х

,.....,=

,.....,=

=

= = =

=

=

Опр. - исправленная выборочная дисперсия

n/n-1 - поправка Бесселя

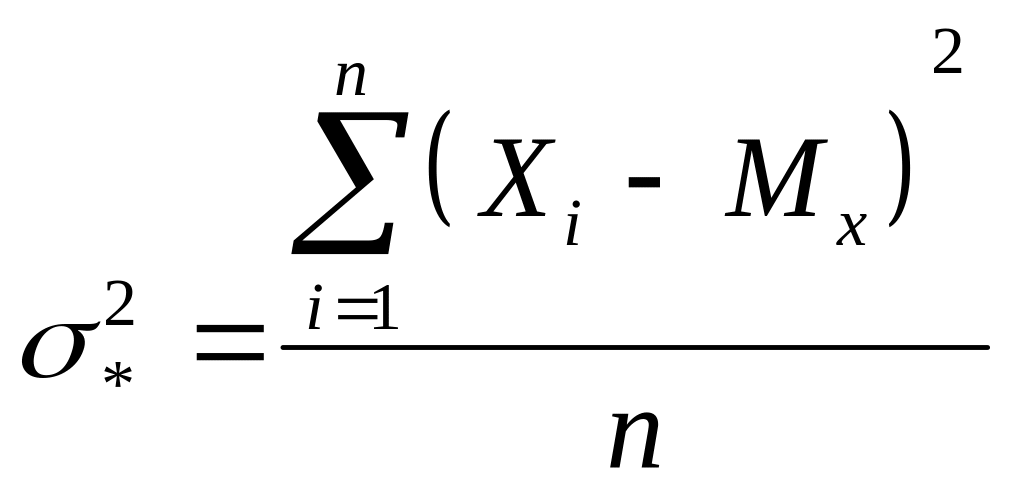- несмещенная оценка

9.4Метод наибольшего правдоподобия.

Основным способом получения оценок параметров генеральной совокупности по данным выборки является метод наибольшего правдоподобия. Этот метод был разработан выдающимся английским математиком Р.А.Фишером.

-независимые набл. над случ. величиной Х

	- вероятность значения,если Х – дискретная
	-плотность распределения, если Х - непрерывная

- функция правдоподобия

Оценка берется, как ,при котором L принимает максимальное значение.

называется оценкой наибольшего правдоподобия.

= 0

9.5Распределение средней арифметической для выборок из нормальной совокупности. Распределение Стьюдента.

Теорема 2.4 Если случайная величина Х подчиняется нормальному закону распределения с параметрами , а - ряд независимых наблюдений над случайной величиной Х, каждое из которых имеет те же числовые характеристики, что и Х, т.е.

,.....,=

,.....,=

то выборочная средняя также подчиняется нормальному закону распределения.

В литературе по статистике приводится таблица нормального распределения с параметрами (0, 1), т.е. , в нашем случае параметры равны:

Поэтому нам необходимо найти связь между нашим распределением и табличным, т.е. нам нужно знать как выражается наша случайная величина через случайную величину подчиняющуюся табличному распределению.

Нормированное отклонение подчиняется нормальному закону распределения.

M ( ) =

D( )=

Пример Автомат штампует детали. Контролируется длина детали, которая подчиняется нормальному закону распределения. Найти вероятность того, что средняя длина деталей, отобранных случайным образом, отклонится от математического ожидания более, чем на 2 мм, если дисперсия случайной величины Х равна 9 кв. мм, а количество деталей в выборке n=16.

Решение

Т.к. детали отбираются независимо друг от друга, то случайная величина имеет нормальное распределение с мат. ожиданием и дисперсией кв.мм

Теперь найдем вероятность того, что

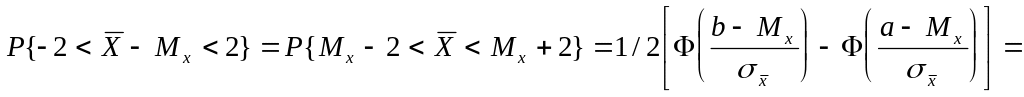
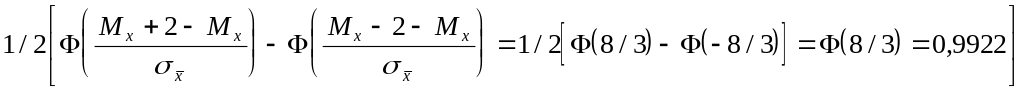
Итак, если случайная величина Х подчиняется нормальному закону распределения, то нормированное отклонение также подчиняется этому закону.

Однако дисперсия почти всегда оказывается неизвестной.

Большой практический интерес имеет распределение Стьюдента.

где -несмещенная и состоятельная оценка дисперсии, вычисленная по выборочным данным.

В литературе по мат. статистике доказывается, что дифференциальная функция t - распределения Стьюдента имеет вид ,

где - коэффициент, зависящий только от объёма n

t - текущая переменная

n - величина объёма

Для этой функции составлены таблицы

Из анализа табличных данных видно, что уже при n=50 распределение Стьюдента мало отличается от нормального.