7.8Закон распределения и числовые характеристики n-мерного случайного вектора.

Функция распределения:

Свойства функции распределения:

1. F(х₁, х₂,..., х_n) – неубывающая функция любого из своих аргументов

2. При х_i = - F (...)=0

3. Функция распределения подсистемы (подмножества) (Х₁, Х₂,..., Х_n) системы (Х₁, Х₂,..., Х_R,..., Х_n) определяется, если положить аргументы, соответствующие остальным случайным величинам Х_R+1,..., Х_n равными +.

F_1,2,...,R (x₁,..., x_R)=F(x_1,..., x_R,+ ,...,+)

4. Функция распределения F(x₁,...,x_n) – непрерывна слева по каждому из аргументов.

Замечание: Если Х₁, Х₂,..., Х_n – независимы, то

F(x₁, x₂,..., x_n) = F₁ (x₁) F₂ (x₂)... F_n (x_n)

Опр. Плотностью распределения системы из n непрерывных с.в. (Х₁, Х₂,..., Х_n) называется n-я смешанная частная производная функции распределения, взятая один раз по каждому аргументу.

Свойства сов. плотности распределения:

1. f(x₁, x₂,..., x_n) 0

2. 

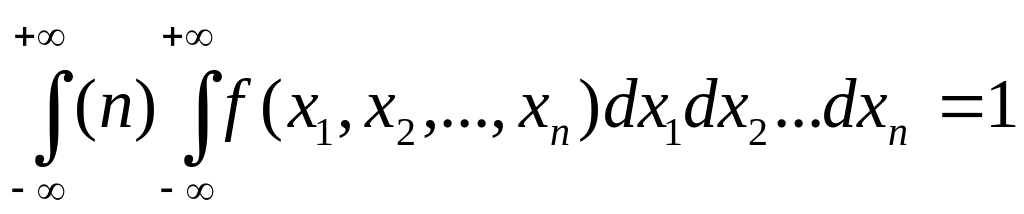
Опр. Условной плотностью распределения любой подсистемы (Х₁, Х₂,...,Х_R) входящей в систему (х₁, х₂,...,х_n), называется плотностью распределения этой подсистемы, вычисленная при условии, что остальные случайные величины приняли определенные значения:

Х_R+1=x_R+1, Х_R+2=x_R+2;...; Х_n=x_n.

Для системы (Х₁, Х₂,..., Х_n) существуют числовые характеристики:

1. n м.о.: М₁ = М[X₁],..., М_n=M[X_n]

2. n дисперсий: D₁=D[X₁],..., D_n=D[X_n]

3. n(n-1) ковариаций:

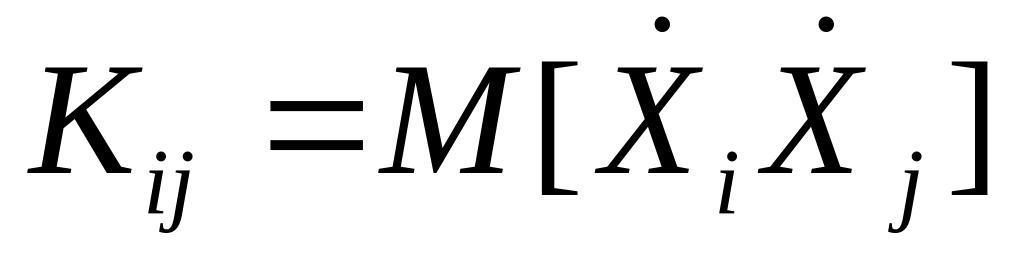
Если учесть, что К_{i j} = D_i, то можно построить матрицу.

Опр. Матрица ковариаций – матрица, компонентами которой являются ковариации К_{i j.}

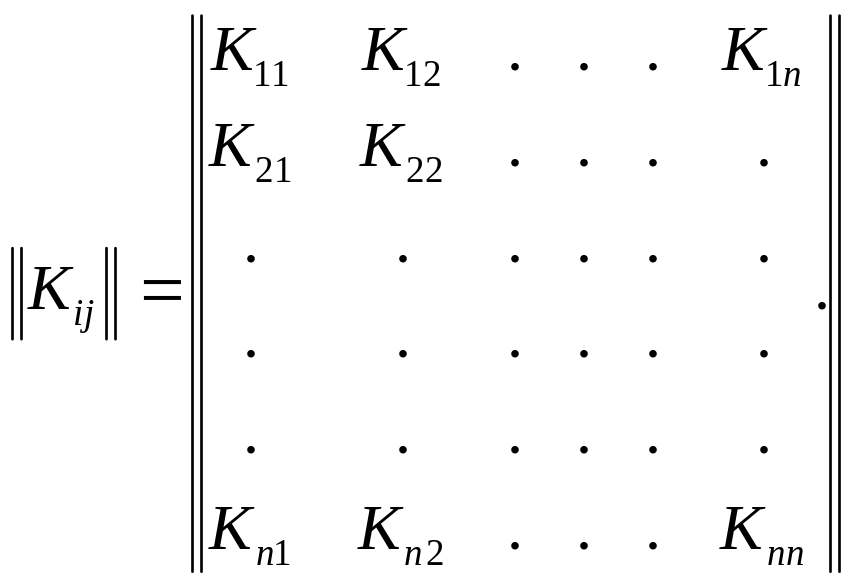
Если с.в. (Х₁, Х₂,..., Х_n) попарно не коррелированы, то их ковариации образуют диагональную матрицу.

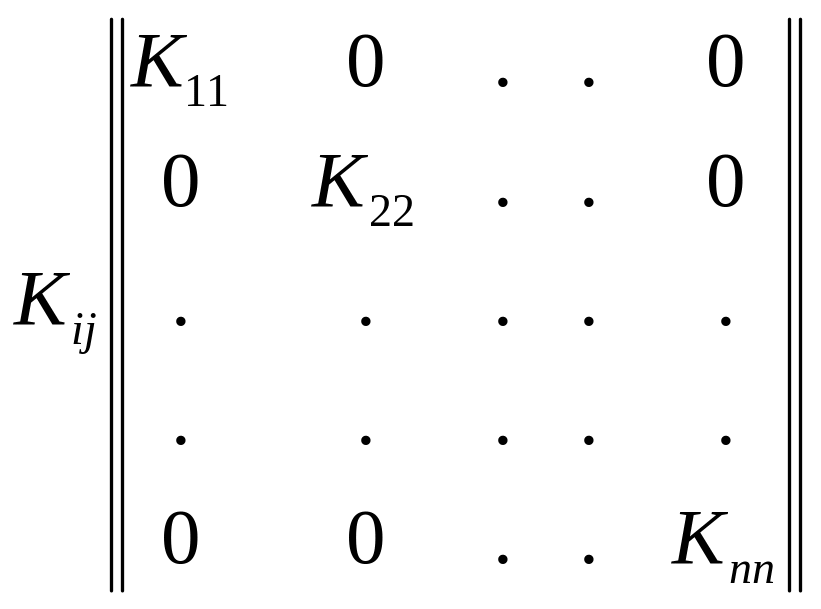
Зная закон распределения системы величин (Х₁, Х₂,..., Х_n), можно найти все ее числовые характеристики:

Лекции « Теория вероятности и математическая статистика »

Раздел 2

«Математическая статистика.» Глава 8Основы математической теории выборочного метода.

8.1Понятие о выборочном методе. Способы образования выборочной совокупности.

Опр. Математической статистикой называется наука, занимающаяся методами обработки опытных данных, полученных в результате наблюдений над случайными явлениями.

Экономически невыгодно производить обследование всей совокупности, если по результатам изучения сравнительно небольшой части её можно получить с достаточной для практики достоверностью необходимую информацию о всей совокупности. Такой метод исследования носит название выборочного. Он нашел широкое применение.

Опр. Вся подлежащая изучению совокупность объектов называется генеральной совокупностью. Та часть объектов, которая попала на проверку называется выборочной совокупностью или просто выборкой. Число элементов в генеральной совокупности и выборке называется их объемами.

Рассмотрим следующие виды выборок:

1) собственно-случайная

2) механическая

3) типическая

4) серийная

Опр. Собственно-случайной называется выборка, в которую члены из генеральной совокупности отбираются совершенно произвольно.

Опр. Механической называется выборка, в которую члены из генеральной совокупности отбираются через определенный интервал.

Опр. Если генеральную совокупность предварительно разбить на непересекающиеся группы, а затем образовать собственно-случайные выборки (с повторным или бесповторным отбором членов) из каждой группы и все отобранные элементы считать попавшими в выборку, то получим выборочную совокупность, которая называется типической.

Опр. Если генеральную совокупность предварительно разбить на непересекающиеся группы, а затем, рассматривая серии как элементы, образовать собственно-случайные выборки (с повторным или бесповторным отбором) и все члены отобранных серий считать попавшими в выборку, то получим выборочную совокупность, которая называется серийной.