7.6Числовые характеристики системы двух с.В. Ковариация и коэффициент корреляции.
Опр. Начальным моментом порядка k,s системы двух с.в.(Х,У) называется математическое ожидание произведения XkYs
k,s=M[XkYs]
Опр. Центральным моментом порядка
k,s
системы двух с.в. (Х,У) называется
математическое ожидание произведения
на
где
=X-Mx;
=Y-My
- центрированные с.в.
Для дискретных с.в. (Х,У):
Для системы непрерывных с.в. (Х,У):
Примечание:
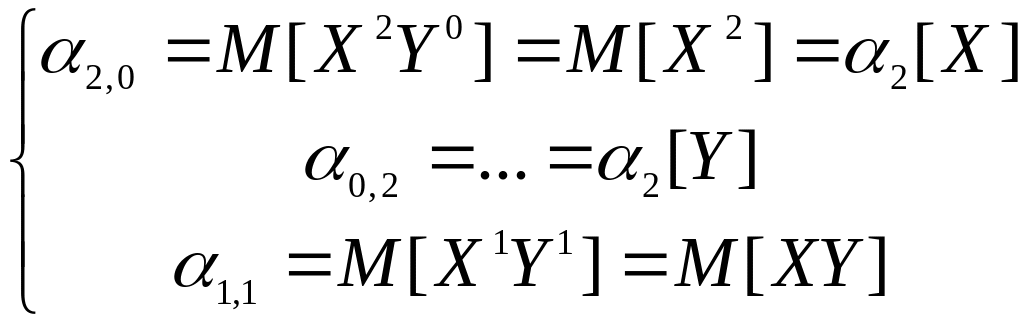
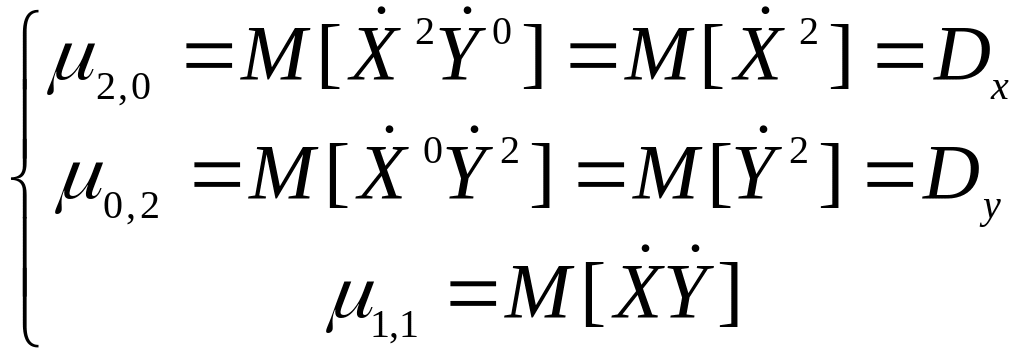
Опр. Ковариацией (корреляционным
моментом) с.в. Х,У называется мат. ожидание
произведения центрированных с.в.
и
.
Замечание:
Для независимых с.в. доказано, что f(x,y)=f1(x)f2(y)
\\ \\
0
Замечание: Ковариация двух с.в равна математическому ожиданию их произведения минус произведение математических ожиданий.
М[X,Y]
//
// \\ \\
MxMy MxMy 1
Опр. Коэффициентом корреляции называется ковариация обезразмеренная делением на средние квадратичные отклонения с.в. Х и У:
Замечание: величина rxy характеризует степень зависимости этих величин, причем только в линейной зависимости, проявляющейся в том, что при возрастании одной с.в. другая проявляет тенденцию также возрастать, если rxy >0, и убывать, если rxy < 0.
Модуль коэффициента корреляции случайных величин Х и У характеризует степень тесноты линейной зависимости между ними.
Если линейной зависимости нет, rxy =0. Если между с.в. существует жесткая функциональная линейная зависимость: У=аХ + b,
то rxy=+ 1 при а>0 и rxy =-1 при а< 0
Опр. Если ковариация Kxy двух с.в. равна нулю, с.в. Х и У называются некоррелированными; если же не равна нулю - коррелированными.
7.7Условные числовые характеристики системы случайных величин (х,у). Регрессия.
Опр. Условным математическим ожиданием одной из с.в, входящих в систему (Х,У), называется её мат. ожидание, вычисленное при условии, что другая с.в. приняла определенное значение, т.е. найденное на основе условного закона распределения.
Для двух дискретных с.в.:
где pyj | xi=P{Y=yj| X=xi}
pxi | yj=P{X=xi| Y=yj}
Для двух непрерывных с.в.:
Опр. Условное мат. ожидание с.в. У при заданном Х=х: M[Y|x]=My|x называется регрессией У на х. Графики этих зависимостей от х и у называются линиями регрессии.
Пример:
Матрица распределения системы двух с.в. (Х,У) задана таблица:
-
(Х,У):
xi | yj
0
2
5
1
0.1
0
0.2
2
0
0.3
0
4
0.1
0.3
0
1) Найти числовые характеристики системы (Х,У):
Mx, My, Dx, Dy, x, y, Kxy, rxy
2) Построить линии регрессии У на Х и Х на У соответственно.
Решение: 1) Ряды отдельных величин:
Px1=P{X=1}=0.1+0.2=0.3
Px2=P{X=2}=0.3
Px3=P{X=4}=0.1+0.3=0.4
X:
-
1
2
4
0,3
0,3
0,4
Мх=1*0,3+2*0,3+4*0,4=2,5
2[X]=12*0,3+22*0,3+42*0,4=7,9
Dx=2[X]- Мх=1.65
x=
=1.285
Py1=P{Y=0}=0.1+0.1=0.2
Py2=P{Y=2}=0.3+0.3=0.6
Py3=P{Y=5}=0.2
-
Y:
0
2
5
0.2
0.6
0.2
My=2*0.6+5*0.2=2.2
2[X]=22*0.6+52*0.2=7.4
Dy=2[Y]- Мy=7.4-(2.2)2=2.56
x= =1.6
M[XY]=2*2*0.3+2*4*0.3+1*5*0.2=4.6
Kxy=4.6-2.5*2.2=-0.9
Между Х и У существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет некоторую тенденцию уменьшаться.
2)
Py1|x1=P{Y=0|X=1}=0.1/0.3=1/3
Py2|x1=P{Y=2|X=1}=0/0.3=0
Py3|x1=P{Y=5|X=1}=0.2/0.3=2/3
My|x1=5*2/3=10/3
Py1|x2=0 Py2|x2=1 Py3|x2=0 My|x2=2
Py1|x3=1/4 Py2|x3=3/4 Py3|x3=0 My|x3=3/2
Также
Pх1|у1=1/2 Pх2|у1=0 Pх3|у1=1/2 Мх|у1=2,5
Pх1|у2=0 Pх2|у2=1/2 Pх3|у2=1/2 Мх|у2=3
Pх1|у3=10 Pх2|у3=0 Pх3|у3=0 Мх|у3=2