Глава 7Системы случайных величин (случайные векторы).

7.1Понятие о системе случайных величин.

Примеры систем с. в.:

1. Точка приземления космического аппарата (Х- широта, У- долгота)

(Х, У) – система с.в.

2. Успеваемость студента характеризуется системой из n случайных величин Х₁, Х_2, …, Х_n – оценками по пятибалльной системе.

3. и т. д.

Геометрически систему (Х, У) можно изобразить совокупностью точек с координатами Х и У.

Опр. Случайным вектором системы (Х, У) называется вектор, начинающийся в начале координат заканчивающийся в точке с координатами (Х,У).

Аналогично:

7.2Функция распределения системы двух случ. Величин.

Опр. Функцией распределения (или «совместной функцией распределения») системы двух случ. величин (Х,У) называется вероятность выполнения двух неравенств:

X<x; Y<y: F(x,y) = P{ X<x; Y<y}

С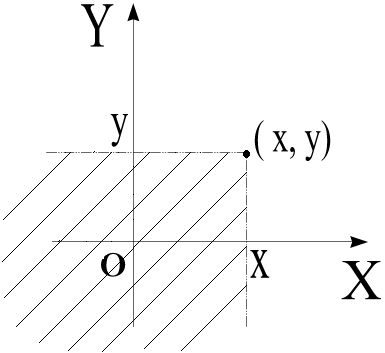 войства функции распределения:

1. F(x,y) – неубывающая функция обоих аргументов, т.е.

при х₂>x₁ F(x₂,y) F(x₁,y)

при y₂>y₁ F(x,y₁) F(x,y₂)

2. Если хотя бы один из аргументов обращается в -, функция распределения равна нулю:

F(x, -)=F(-,y)=F(-,-)=0

3. Если оба аргумента равны +, функция распределения равна единице:

F(+,+)=1

4. Если один из аргументов обращается в +, функция распределения F(x,y) становится равной функции распределения случ. величины соответствующей другому аргументу:

где F₁(x) и F₂(у) – функции распределения с.в. Х и У соответственно:

F₁(x)=P{X<x} F₂(y)=P{Y<y}

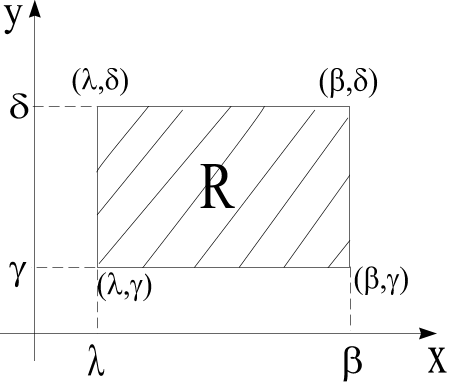
7.3Система двух дискретных случ. Величин. Матрица распределения.

Х: { x₁, x₂,…, x_n} Y: { y₁, y₂,…, y_m}

P_ij=P{X=x_i; Y=y_j}

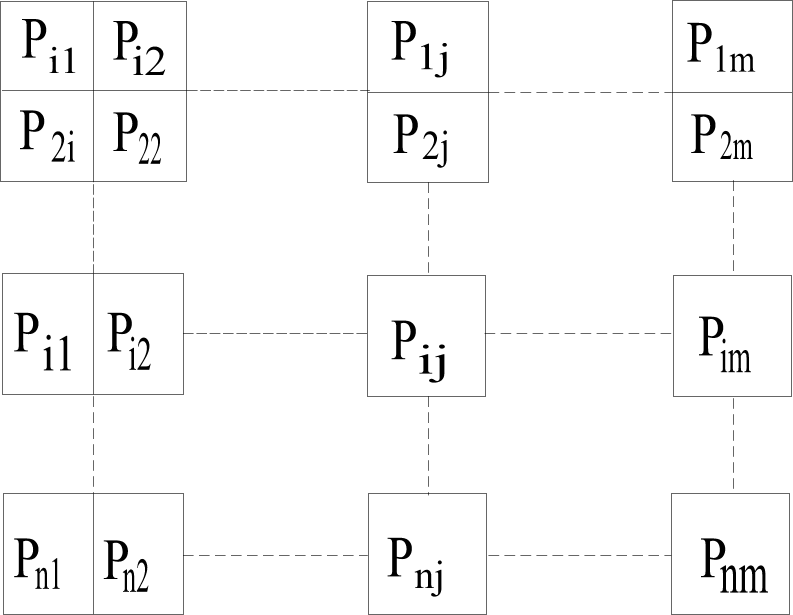
Опр. Матрицей распределения двух дискретных сл. величин называется прямоугольная таблица, в которой записаны все вероятности p_ij(i=1, …,n; j=1,…,m).

7.4Система двух непрерывных случ. Величин. Совместная плотность распределения.

Опр. Система двух с.в. называется непрерывной, если её функция распределения F(x,y) есть непрерывная функция, дифференцируемая по каждому из аргументов, у которой существует вторая смешанная производная .

Обе составляющие системы Х и У представляют собой непрерывные с. величины.

Опр. Плотностью распределения (совместной плотностью) для системы двух непрерывных с.в. (Х,У) назовем предел отношения вероятности попадания случайной точки (Х,У) в элементарный прямоугольник, примыкающий к точке (х,у), к площади этого прямоугольника, когда оба эти размера стремятся к нулю.

Свойства плотности распределения:

1. f (x,y)  0

2. 

Опр. Геометрически совместная плотность f(x,y) системы двух с.в. (Х,У) изображается поверхностью распределения.

Опр. Элементом вероятности называется вероятность попадания с.в. (Х,У) в элементарный прямоугольник со сторонами dx и dy.

P{(x,y)dS}=f(x,y)dxdy

Замечание:

Для того, чтобы получить плотность распределения одной из величин, входящих в систему, надо проинтегрировать совместную плотность в бесконечных пределах по аргументу, соответствующему другой случайной величине.

7.5Зависимые и независимые случ. Величины. Условные законы распределения.

Опр. Две с.в. Х и У называются независимыми, если независимы все связанные с ними события.

Замечание: Так как зависимость и независимость событий всегда зависимы, то зависимость и независимость с.в. также всегда взаимны.

Другое опр. Две с.в. называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая.

Функция распределения:

F(x,y)=P{X<x; Y<y}=P{X<x}P{Y<y}, т.к. {X<x} и {Y<y} независимы

 p_ij=P{X=x_i}P{Y=y_j}=p_xip_yj

Плотность распределения независимых с.в.:

где f₁(x) – плотность распределения с.в. Х

f₂(x) - плотность распределения с.в. У

Опр. Уловным законом распределения одной из величин (Х,У), входящих в систему, называется её закон распределения, вычисленный при условии, что другая с.в. приняла определенное значение.

Функция распределения для любых с.в.:

F(x,y)=P{X<x;Y<y}=P{X<x}P{Y<y|X<x}=P{Y<y}P{X<x|Y<y}=

=F₁(x)P{Y<y|X<x}

Опр. Условной функцией распределения с.в. У называется условная вероятность P{Y<y|X<x}, т.е. вероятность события {Y<y} при условии, что величина Х приняла значение меньше, чем х.

P{Y<y|X<x}=F₂(y|X<x)

Тогда F(x,y)=F₁(x)F₂(y,X<x)= F₂(y)F₁(x,Y<y)

Теорема умножения плотностей:

Рассмотрим систему двух зависимых непрерывных с.в. (Х,У) и докажем, что их совместная плотность равна произведению плотности одной из них на условную плотность другой при заданном значении первой:

f(x,y)=f₁(x)f₂(y|x)=f₂(y)f(x|y)

Док-во:

Рассмотрим элемент вероятности f(x,y)dxdy, т.е. вероятность попадания:

A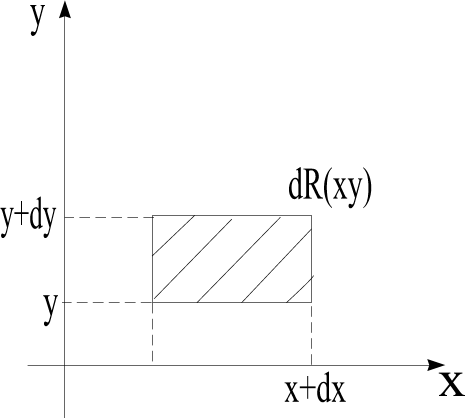 ₁={X(x,x+dx)}

A2={Y(y,y+dy)}

f(x,y)dxdy=P(A₁)P(A₂|A₁)=P{X(x,x+dx)}P(Y(y+dy)|X(x+dx)}

Теперь: dx и dy  0

F(x,y) dx dy=f₁(x) dx f₂(y|dx) dy  f(x,y)=f₁(x) f₂(y|x)

Свойства условной вероятности:

f₂(y|x)0

f₁(x|y)0