6.2Показательное распределение.

О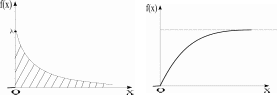 пр. Непрерывная с. в. Х имеет показательное распределение (или экспоненциальное) распределение, если:

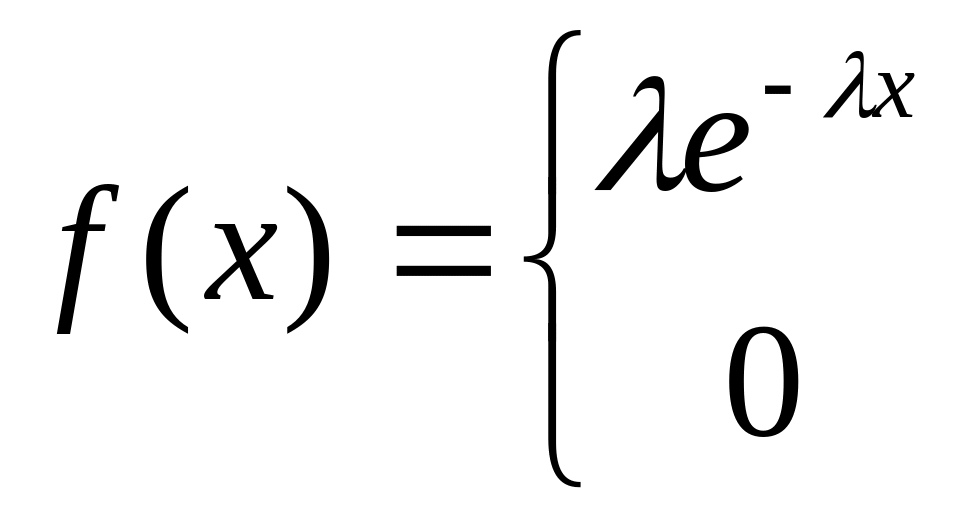
	х > 0
	x  0

т.е. мат. ожидание с. в., имеющей показательное распределение, обратно его параметру .



т. е. среднее квадратичное отклонение с. в. Х, имеющей показательное распределение, равно её мат. ожиданию.

Для нахождения асимметрии:

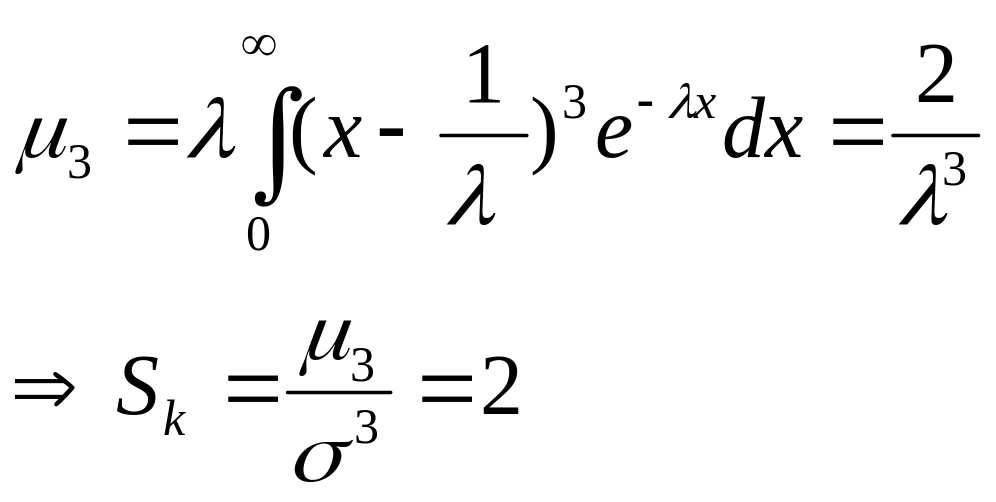
Показательное распределение тесно связано с простейшим потоком событий.

Теорема:

И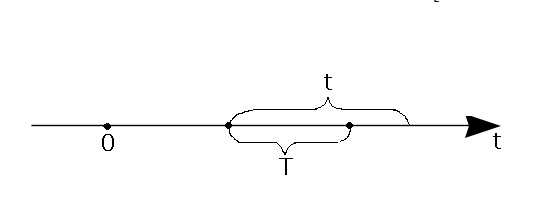 нтервал времени Т между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока: (t > 0)

Док–во:

F (t) = P { T < t }

Для того, чтобы выполнялось неравенство T < t, нужно, чтобы хотя бы одно событие потока попало на участок длины t;

Вероятность этого:

• 

• 

Замечание:

При изменении m кривая f(x), не изменяя своей формы, просто будет смещаться вдоль оси абсцисс.

Изменение  равносильно изменению масштаба кривой по обеим осям.

6.3Нормальное распределение.

Опр. С. в. Х имеет нормальное распределение с параметрами m, , если её плотность распределения имеет вид:

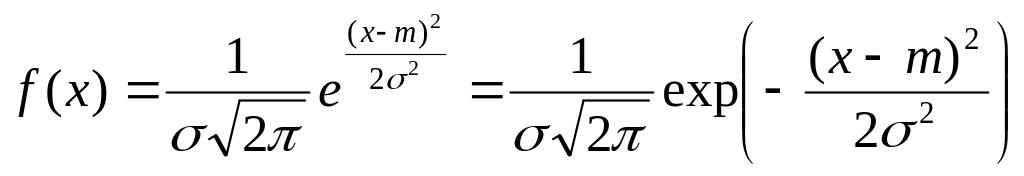
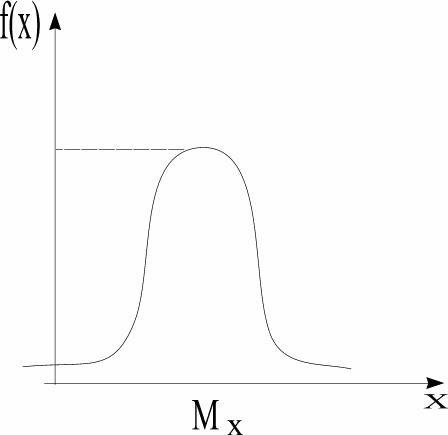
Мода x_m = m

т. к. график f(m) симметричен, то

M_x = x_m = m

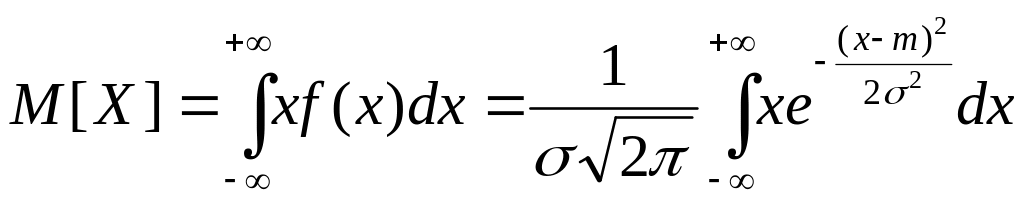
Замена переменной t=(x-m)/



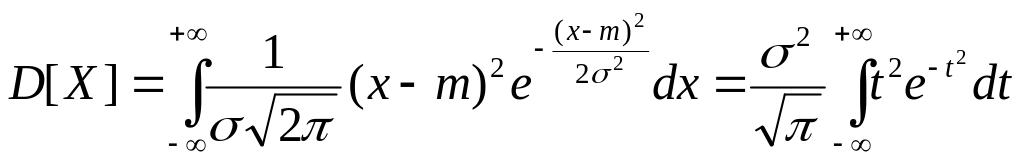
Интегрируя по частям:

 среднее квадратичное отклонение _х = 

Центральный момент S- го порядка:

Делаем замену переменной:

При нечётном S _S = 0 (интервал в симметричных пределах от нечётной функции равен нулю).

При чётных S: (интегрирование по частям)

т. к.



т. к. ₀ = 1  ₂ = ²  ₄ = 3⁴  ₆ = 15⁶ …

Эксцесс:

Вероятность попадания на участок от  до :

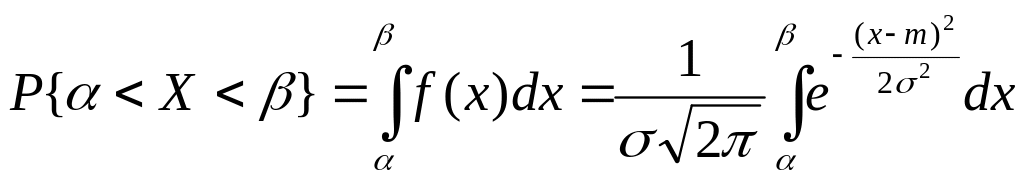
Замена переменных:

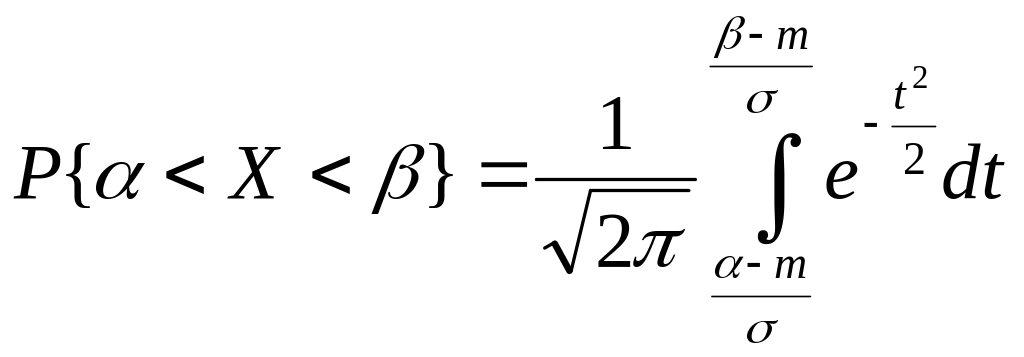
Как известно, неопределённый интеграл не выражается через элементарные функции, но его можно выразить через специальную функцию:

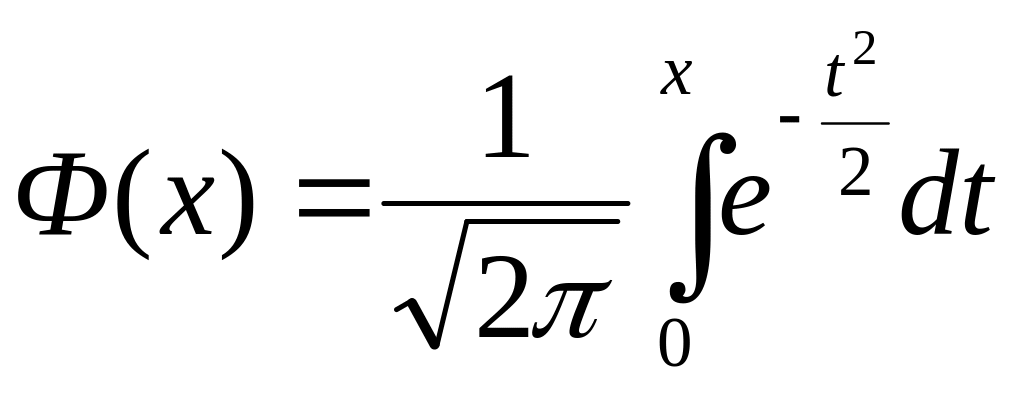- функция Лапласа (или «интеграл вероятностей»)

Для неё составлены таблицы.



Свойства функции Лапласа:

1. Ф (0) = 0

2. Ф (- х) = - Ф (х) - нечётная функция

3. Ф (+ ) = 0,5  Ф (- ) = - 0,5

Док – во:

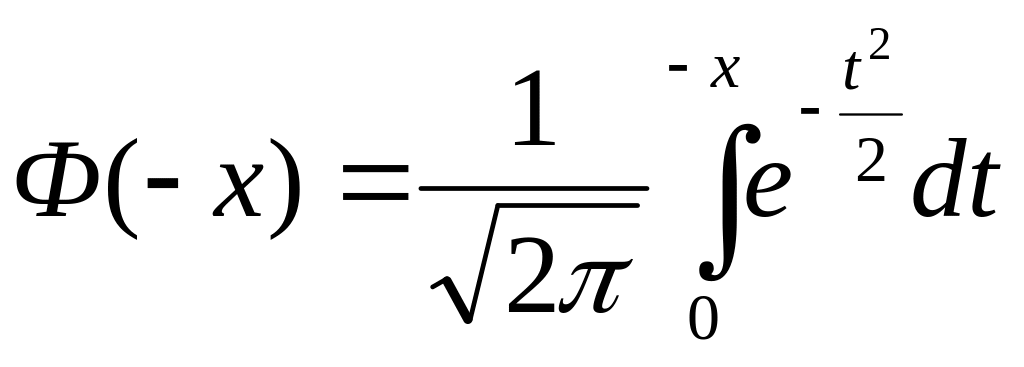
Делаем замену -t = z

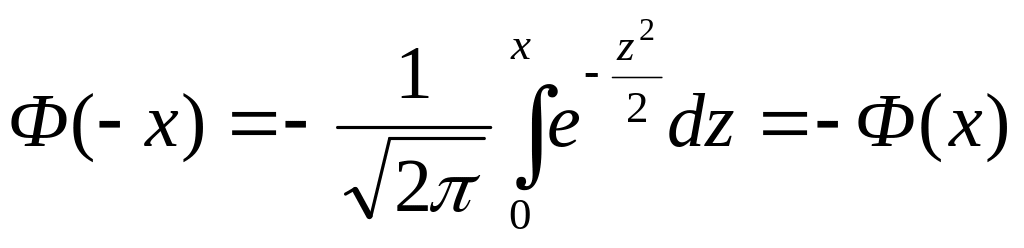
3-е свойство вытекает из интеграла Эйлера - Пуассона:



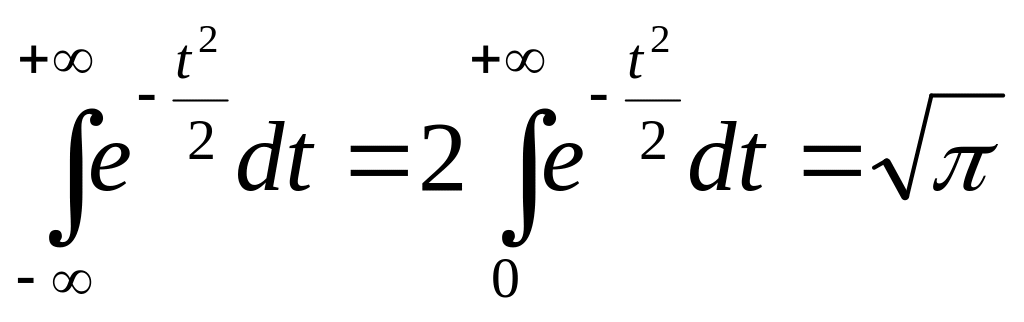
 Ф (+ ) = 1/2

Функция распределения:

Замечание:

Нормальное распределение возникает в тех случаях, когда складывается много независимых с. в. Х₁, Х₂,…, Х_n. Тогда, каковы бы ни были с. в. Х₁, Х₂,…, Х_n, закон распределения их суммы будет близок к нормальному.

6.4Гамма - распределение и распределение Эрлана.

Опр. Неотрицательная с. в. Х имеет гамма - распределение, если её плотность распределения выражается формулой:

(х > 0)

где  > 0, k > 0, Г (k) – гамма – функция

Свойства гамма – функции:

1. Г (k+1) = k Г (k)

2. Г(1) = 1  Г (k+1) = k!

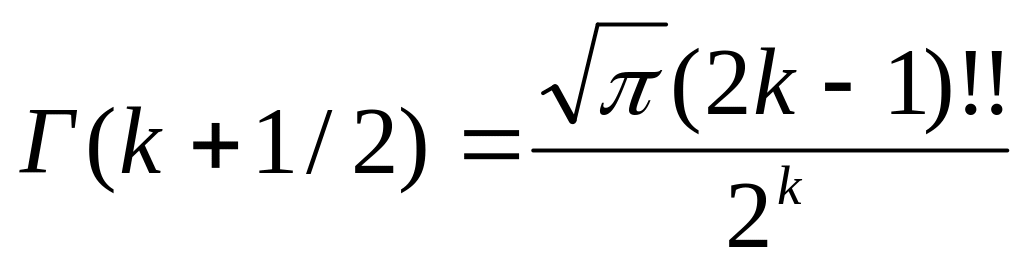3. , где (2k –1) !! = 1*3*5*…*(2k – 1)

Числовые характеристики:



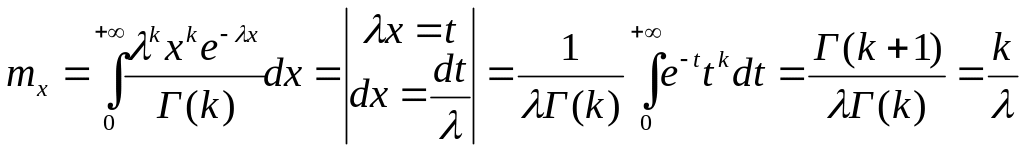
Замечание:

При k = 1 гамма - распределение превращается в показательное: x > 0

Опр. При целом k > 1 гамма – распределение превращается в распределение Эрлана k – го порядка.

Замечание: Закону Эрлана k – го порядка подчинена сумма независимых с. в. Х₁ + Х₂ + … + Х_k, каждая из которых распределена по показательному закону с параметром .