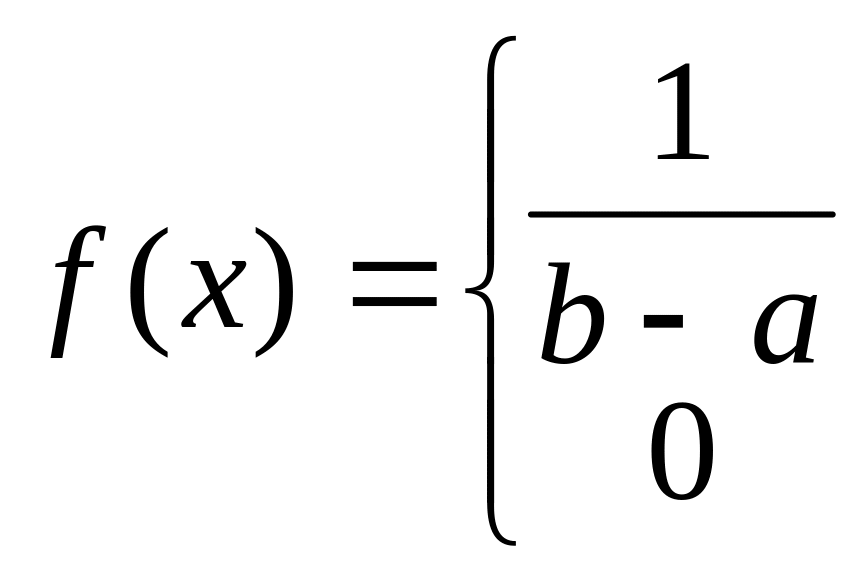- •Содержание
- •Введение
- •Глава 1 Основные понятия.
- •1.1Вводные понятия.
- •1.2Непосредственный подсчёт вероятностей
- •1.3Частота или статическая вероятность.
- •Глава 2Аксиоматика теории вероятности. Правила умножения и сложения и их свойства.
- •2.1Элементарные сведения из теории множеств.
- •2.2Аксиомы теории вероятностей и их следствия. Правило сложения вероятностей.
- •2.3Комбинаторика. Классические модели. Примеры.
- •2.4Геометрическая модель.
- •2.5Условная вероятность события. Правило умножения вероятностей.
- •2.6Формула полной вероятности.
- •2.7Теорема гипотез (Формула Бейеса).
- •Глава 3Случайные величины, их законы распределения.
- •3.1Понятие случайной величины. Законы распределения. Ряд распределения дискретной случайной величины.
- •3.2Функция распределения случайной величины. Её свойства.
- •3.3Функция распределения дискретной с. В. Индикатор события.
- •3.4Непрерывная случайная величина. Плотность распределения.
- •Глава 4Числовые характеристики случайных величин.
- •4.1Роль и назначение числовых характеристик. Математическое ожидание случайной величины.
- •4.2 Моменты. Дисперсия. Среднее квадратичное отклонение.
- •Глава 5Некоторые важные для практики распределения дискретных с. В.
- •5.1Аппарат производящей функции.
- •5.2Испытания Бернулли.
- •5.3Биноминальное распределение.
- •5.4Распределение Пуассона.
- •5.5Геометрическое распределение.
- •5.6Гипергеометрическое распределение.
- •Глава 6Некоторые важные для практики распределения непрерывных случайных величин.
- •6.1Равномерное распределение.
- •6.2Показательное распределение.
- •6.3Нормальное распределение.
- •6.4Гамма - распределение и распределение Эрлана.
- •Глава 7Системы случайных величин (случайные векторы).
- •7.1Понятие о системе случайных величин.
- •7.2Функция распределения системы двух случ. Величин.
- •7.3Система двух дискретных случ. Величин. Матрица распределения.
- •7.4Система двух непрерывных случ. Величин. Совместная плотность распределения.
- •7.5Зависимые и независимые случ. Величины. Условные законы распределения.
- •7.6Числовые характеристики системы двух с.В. Ковариация и коэффициент корреляции.
- •7.7Условные числовые характеристики системы случайных величин (х,у). Регрессия.
- •7.8Закон распределения и числовые характеристики n-мерного случайного вектора.
- •Лекции « Теория вероятности и математическая статистика »
- •Раздел 2
- •«Математическая статистика.» Глава 8Основы математической теории выборочного метода.
- •8.1Понятие о выборочном методе. Способы образования выборочной совокупности.
- •8.2Характеристики генеральной и выборочной совокупности.
- •8.3Эмпирическая функция распределения.
- •Глава 9Статистическое оценивание параметров распределения.
- •9.1Понятие об оценке параметров.
- •9.2Основные свойства оценок.
- •1) Несмещенность
- •2) Эффективность
- •3) Состоятельность
- •9.3Оценка математического ожидания и дисперсии по выборке.
- •9.4Метод наибольшего правдоподобия.
- •9.5Распределение средней арифметической для выборок из нормальной совокупности. Распределение Стьюдента.
- •9.6Распределение дисперсии в выборках из нормальной генеральной совокупности. Распределение Пирсона.
- •9.7Понятие доверительного интервала. Доверительная вероятность.
- •9.8 Построение доверительного интервала для математического ожидания при известной .
- •9.9Построение доверительного интервала для математического ожидания при неизвестной .
- •9.10Построение доверительного интервала для дисперсии.
- •Глава 10Проверка статистических гипотез.
- •10.1Понятие статистической гипотезы. Общая постановка задачи проверки гипотез.
- •10.2Проверка гипотезы о равенстве центров распределений двух нормальных генеральных совокупностей при известном .
- •10.3Проверка гипотезы о равенстве центров распределения нормальных генеральных совокупностей при неизвестном .
- •10.5Проверка гипотез о законе распределения. Критерий согласия .
- •10.6Вычисление объёма выборки.
- •Глава 11Основы дисперсионного анализа.
- •11.1Основная идея дисперсионного анализа.
- •11.2Однофакторный комплекс.
- •11.3Двухфакторный комплекс.
- •11.4Дисперсионный анализ с равным числом наблюдения в ячейке.
- •11.5Дисперсионный анализ с неравным числом наблюдений в ячейке.
- •Глава 12Основы корреляционного анализа.
- •12.1О связях функциональных, стохастических, статистических и корреляционных.
- •12.2Определение формы связи. Понятие регрессии.
- •12.3 Поле корреляции.
- •12.4Линейная регрессия. Понятие о способе наименьших квадратов.
- •12.5Кривые регрессии. Нелинейная регрессия.
- •12.6Измерение тесноты связи. Эмпирическое корреляционное отношение.
5.5Геометрическое распределение.
Опр. С. в. Х имеет геометрическое распределение, если её возможные значения 0, 1, 2, …, m, …, а вероятности этих значений: Pm=qmp, где 0 < p < 1; q = 1-p; m = 0, 1, 2, …
Замечание:
Вероятности Pm образуют геометрическую прогрессию с первым членом p и знаменателем q.
Задача:
Проведение опыта с двумя исходами до первого нужного.
p – вероятность « успеха », q – « неудача »
Р0 = р - первая попытка успешна
Р1 = qp - первая – неудача, второй – успех
Х: |
0 |
1 |
2 |
… |
m |
Число « неуспехов » |
p |
qp |
q2p |
… |
qmp |
Производящая функция:
![]()
т. к. p = 1 – q
![]()
![]()
![]()
![]()
![]()
Y =X + 1 – общее число попыток
![]()
![]()
![]()
Пример:
В нашем распоряжении имеется n лампочек, каждая из них с вероятностью p имеет дефект. Лампочка ввинчивается в патрон и в сеть, включается ток, дефектная лампочка перегорает и заменяется другой.
С. в. z – число испробованных лампочек
Нужно построить ряд с. в. z и найти мат. ожидание
Решение:
Пусть q = 1 – p - вероятность работающей лампы
z: |
1 |
2 |
… |
m |
… |
m-1 |
n |
q |
pq |
… |
pm-1q |
… |
pn-2q |
pn-1 |
![]()
![]()
5.6Гипергеометрическое распределение.
Опр. С. в. Х имеет гипергеометрическое
распределение с параметрами a,
b и n, если
её возможные значения 0, 1, …, m,…,а
имеют вероятности:
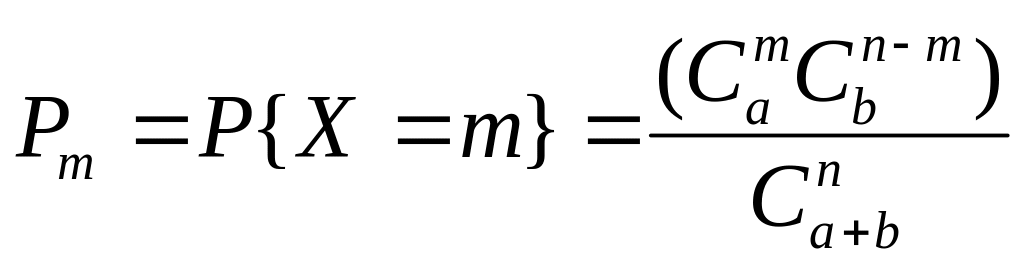 (m = 0, …, а)
(m = 0, …, а)
Пример задачи гипергеометрического распределения:
Имеется урна, в которой a черных шаров и b – белых; из неё вынимается n шаров.
С. в. Х – число белых шаров среди вынутых.
![]()
![]()
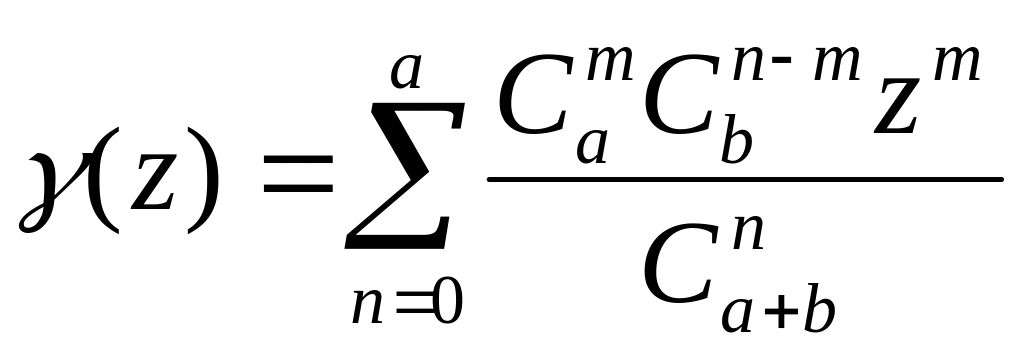
Пример:
В шкафу находятся 9 приборов; из них 5 новых и 4 б/у. Из шкафа наугад вынимаются 4 прибора.
С. в. Х – число новых приборов
Построить ряд распределения Х двумя способами.
Решение:
a=5, b=4, a+b = 9
С49= 9*8*7*6 / 1*2*3*4 =126
P0 = C05*C44 / 126 = 1/126 = 0,008
P1 = C15*C34 / 126 = 5*6/126 = 0,159
P2 = C25*C24 / 126 = 10*6/126 = 0,476
P3 = C35*C14 / 126 = 0,317
P4 = C45*C04 / 126 = 0,040
Х = |
0 |
1 |
2 |
3 |
4 |
0,008 |
0,159 |
0,476 |
0,317 |
0,040 |
mх = 0*0,008+1*0,159+2*0,476+3*0,317+4*0,040=2,222
Также (из гипергеометрической формулы):
mх = 4*5 / 9 = 2,222
Для вычисления дисперсии грубо переносим т. 0 в т. 2
Y: |
-2 |
-1 |
0 |
1 |
2 |
0,008 |
0,159 |
0,476 |
0,317 |
0,040 |
2=(-2)2*0,008+(-1)2*0,159+0,317+4*0,040=0,668
D(Y)=D(X)=0,617
Глава 6Некоторые важные для практики распределения непрерывных случайных величин.
6.1Равномерное распределение.
Опр. С. в. Х имеет равномерное распределение на участке от а до b, если её плотность f(x) на этом участке постоянна:
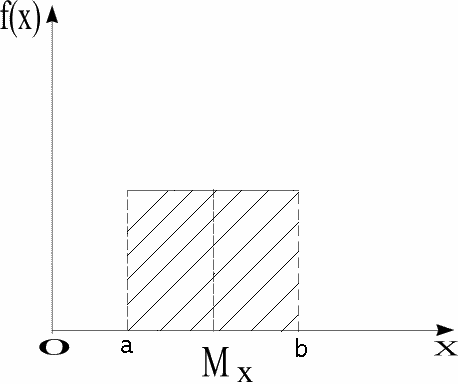
|
при х(a,b) |
при х (a,b) |
![]()
![]()
![]()
Равномерное распределение не имеет моды.
Медиана для симметричного случая совпадает с мат. ожиданием.
Так же подтверждает симметричность и 3=0
Для определения эксцесса найдём 4:
![]()
![]()
Ф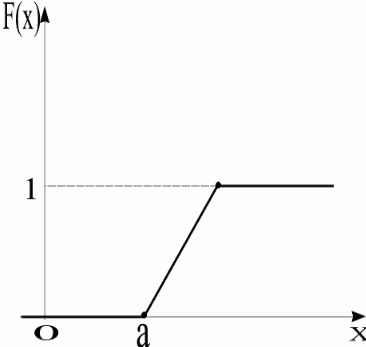 ункция
распределения:
ункция
распределения:
-
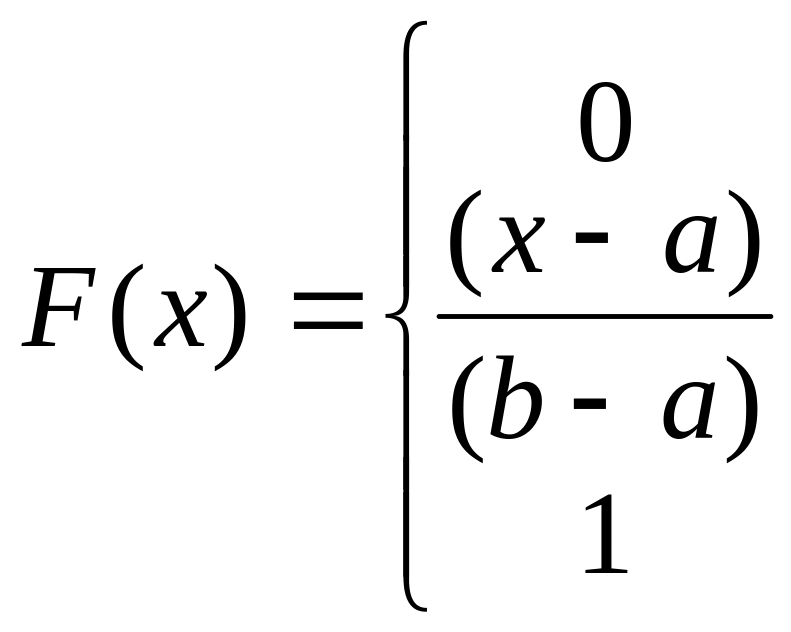
x < a
a < x < b
b < x
Пример по времени.