Глава 5Некоторые важные для практики распределения дискретных с. В.

5.1Аппарат производящей функции.

В ряде случаев при определении важнейших числовых характеристик дискретных с.в. может помочь аппарат производящих функций.

Постановка задачи:

Пусть имеется дискретная с.в. X,

Производящей функцией для с.в. X, принимающей неотрицательные целочисленные значения 0, 1, 2, … , k, … с вероятностями p₀, p₁, p_2, … , , p_k, …; p_k,= P{X=k}, называется

где z – произвольный параметр (0<z≤1).

При z=1:

Возьмём первую производную по z от производящей функции:

При z=1 , а это и есть м.о. с.в. X.

Т.е. мы пришли к выводу: м.о. неотрицательной целочисленной с.величины равно первой производной её производящей функции при z=1.

Возьмём вторую производную по z от производящей функции:

При z=1 , здесь первая из двух сумм, не что иное, как начальный момент второго порядка с.в. X, а вторая сумма – м.о..

Следует

Т.е. мы пришли к выводу: начальный момент второго порядка неотрицательной целочисленной с.величины равен сумме второй и первой производной её производящей функции при z=1.

Аналогично далее третья и четвёртая производная.

5.2Испытания Бернулли.

Опр. Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов оказываются неизменными для всех испытаний.

Обозначим эти вероятности через p и q, и пусть p – «успех» - У

q – «неудача» –Н

Очевидно: p+q =1

Пространство элементарных событий отдельного испытания состоит из двух точек, а n испытаний - из 2ⁿ точек.

Вероятность любой последовательности есть произведение, полученное при замене символов У и Н на p и q соответственно, т. е.

Р{УУНУН … ННУ} = ppqpq … qqp

5.3Биноминальное распределение.

Опр. Дискретная случайная величина Х имеет биноминальное распределение, если её возможные значения: 0,1,…, m, …,n,а соответствующие вероятности: P_m=P{X=m} = C_n^m p^mq^n-m

где

а 0<p<1; q=1-p; m = 0,1, …,n

Теорема: если с. в. Х есть количество успехов в n испытаниях Бернулли, то оно имеет биноминальное распределение:

Док-во:

Пусть произведено n испытаний Бернулли.

Необходимо найти вероятность P_m (события -m успехов)

B₁={УУ…У Н…Н }

 

m (n-m) раз

Точно такую же вероятность имеют и все варианты с m успехами и n-m неудачами.

Число таких вариантов

т.е.

P₀ = qⁿ P_n= P{++…+ } =pⁿ

Если задача ставится как: « не менее m успехов в n опытах », то

R_m=P{xm}=P{x=m}+P{x=m+1}+…+P{x=n}



или

Числовые характеристики биноминального распределения:

Производящая функция:

Мат. ожидание:

Принимая здесь z=1

т.е. M_x = np

Второй начальный момент:

Дисперсия:

Среднее квадратичное отклонение:

5.4Распределение Пуассона.

Опр. С.в. Х имеет распределение Пуассона, если возможные значения: 0,1,2,…,m,…, (бесконечное, но счётное множество значений), а соответствующие вероятности выражаются формулой:

(m = 0,1,2,…)

Распределение Пуассона играет большую роль в практическом применении теории вероятности: многие физические явления приводят к именно такому распределению.

Теорема параметра а:

Параметр а в законе Пуассона является одновременно мат. ожиданием и дисперсией с. в. Х, распределённой по закону Пуассона.

Док-во:

Ряд Тейлора: 

Мат. ожидания:

 M_x= a

;

Второй начальный момент:

Дисперсия:



Среднее квадратичное отклонение:

Теорема: Закон Пуассона является предельным для биноминального распределения при стремлении числа опытов n к бесконечности и стремлении параметра p к нулю, но так, что

Док-во:

Мат. ожидание M_x = np = a 

е^-а

Преобразуем выражение, стоящее под знаком предела: //

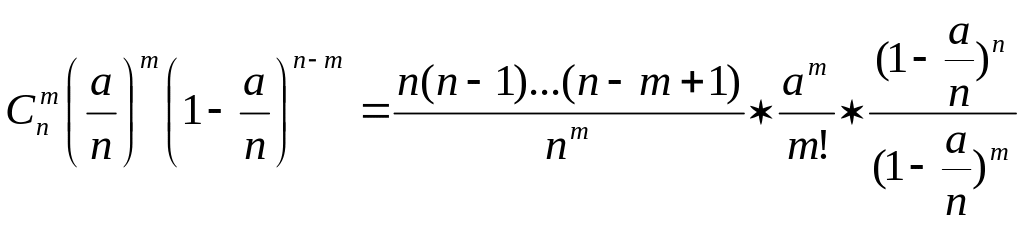
где , ,

а при n   скобка  е^-а 

Замечание:

Распределение Пуассона с параметром a=np можно приближенно применять вместо биноминального, когда число опытов n очень велико, а число p очень мало.

Пример: включение – выключение выключателя.

Рассмотрим задачу:

Пусть на оси времени ot случайным образом возникают точки – моменты появления каких – то однородных событий (например, вызов на телефонной станции, приход посетителей в магазин и т. д.)

Опр. Последовательность таких моментов обычно называют потоком событий.

1. Опр. Стационарность – это свойство означает, что вероятность попадания того или иного числа событий на участок времени длины  не зависит от того, где на оси ot находится этот участок, а зависит только от его длины .

Опр. Интенсивность потока - это среднее число событий, появляющихся в единицу времени  (для стационарного потока =const)

2. Опр. Ординарность – это свойство выражается в том, что вероятность попадания на малый участок t двух или более событий пренебрежительно мала по сравнению с вероятностью попадания на него одного события.

, где n_соб. Число попаданий на отрезке t

3. Опр. Отсутствие последствий - это свойство означает, что вероятность попадания того или иного числа событий на заданный участок оси ot не зависит от того, сколько событий попало на любой другой, не пересекающийся с ним участок (в частности « будущее » потока не зависит от его прошлого).

Опр. Простейшим (или стационарным, пуассоновским) потоком называется поток событий, обладающий свойствами: стационарностью, ординарностью и отсутствием последствий.

Возьмём на оси ot участок времени . Разделим мысленно участок  на n равных частей длины t = / n.

M_xt = t

При очень больших n, учитывая ординарность потока, вероятностью попадания двух событий на участок t можно пренебречь.

При U =1, t – занят; при U = 0, t – пуст.

M [ U ] = p t

c другой стороны: M [ U ] =  t

 - вероятность того, что t занято.

Из свойства «без последствий»  независимость всех участков.



количество занятых ячеек

Замечание:

Для простого потока событий через интервал времени , вероятность, что за это время произойдёт m событий: .

Если закон не удовлетворяет условию стационарности, то в законе Пуассона:

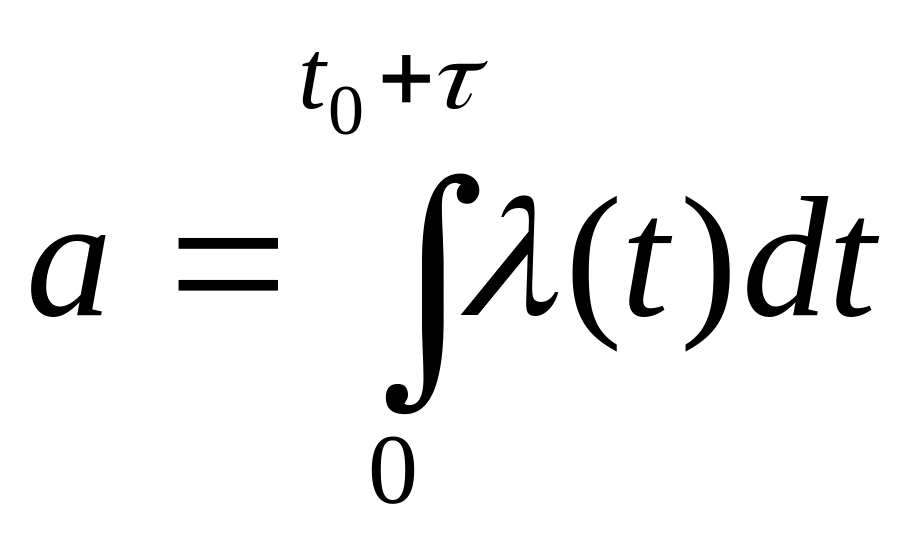
Замечание:

Ось ot необязательно должна быть осью с координатами времени, координаты могут иметь любой физический смысл (например, пространства)

Опр. Интенсивность потока – это среднее число событий на единицу измерения пространства.

Тогда: =f (координаты пространства)

а: а=

Пример:

На автоматическую телефонную станцию поступает простейший поток вызовов с интенсивностью =0.8 вызов \ минута.

Найти вероятность того, что за две минуты:

а) не придёт ни одного вызова

б) придёт ровно один вызов

в) придёт хотя бы один вызов

Решение:

Х – число вызовов за 2 минуты

а=  = 2*0,8=1,6

а) P₀ = а⁰ / 0! * е^-1,6 = е^-1,6 = 0,202

б) Р₁ = а¹ / 1! * е^-1,6 = 1,6*е^-1,6 =0,323

в) Р{X  1 } = 1- P₀ =1- 0.202 = 0.798