3. Усовершенствованный метод Эйлера.
Этот метод построен на правиле трапеций. Вычисления разбивают на два этапа. На первом этапе (этапе прогноза) в соответствии с методом Эйлера вычисляют грубое приближение к значению yi+1:
На втором этапе (этапе коррекции) вычисляют усреднённое значение углового коэффициента, и уточнённое значение yi+1 находят по формуле:
Также, как и предыдущих случаях, используя формулу нахождения погрешности для метода трапеции найдем шаг:
h≤(0.01*12)/(128*3) => h=0.02
Заданный диапазон изменения аргумента [0,7;3,7] разобьем на
150 равных отрезков (шаг h=0.02).
Получаем таблицу значений искомой функции Y(x):
№ х y 0 0.7000 1.30000 1 0.7200 1.31275 2 0.7400 1.32636 3 0.7600 1.34086 4 0.7800 1.35627 5 0.8000 1.37261 6 0.8200 1.38990 7 0.8400 1.40817 8 0.8600 1.42743 9 0.8800 1.44770 10 0.9000 1.46901 ----------------------------------
|
№ х y ------------------------------------- 140 3.5000 13.02192 141 3.5200 13.14730 142 3.5400 13.27268 143 3.5600 13.39805 144 3.5800 13.52341 145 3.6000 13.64874 146 3.6200 13.77403 147 3.6400 13.89929 148 3.6600 14.02449 149 3.6800 14.14965 150 3.7000 14.27475 |
График искомой функции:
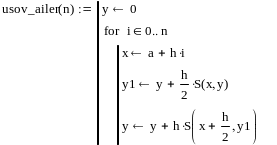
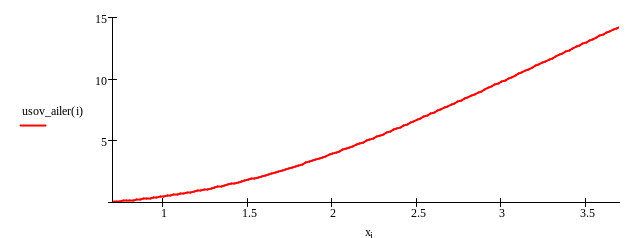
2. Найти решение задачи Коши на интервале (x0-X), используя методы Рунге четвёртого порядка.
Наиболее популярными среди классических явных одношаговых методов являются методы Рунге-Кутта. Метод Эйлера, модифицированный и усовершенствованный методы Эйлера можно рассматривать как простейших представителей этого класса методов.
Метод Рунге-Кутта позволяет строить схемы различного порядка точности. Основная идея метода состоит в построении специального алгоритма, такого, чтобы приращение функции на шаге ∆y=yi+1-yi совпало с приращением ∆y, которое определяется из ряда Тейлора с учётом возможно большего числа членов. При этом вторые и следующие производные рассчитываются не в результате дифференцирования, а путём многократного вычисления функции f(x,y) в некоторых промежуточных точках. Наиболее известным из методов Рунге-Кутта является классический 4-этапный метод четвёртого порядка точности. h5<
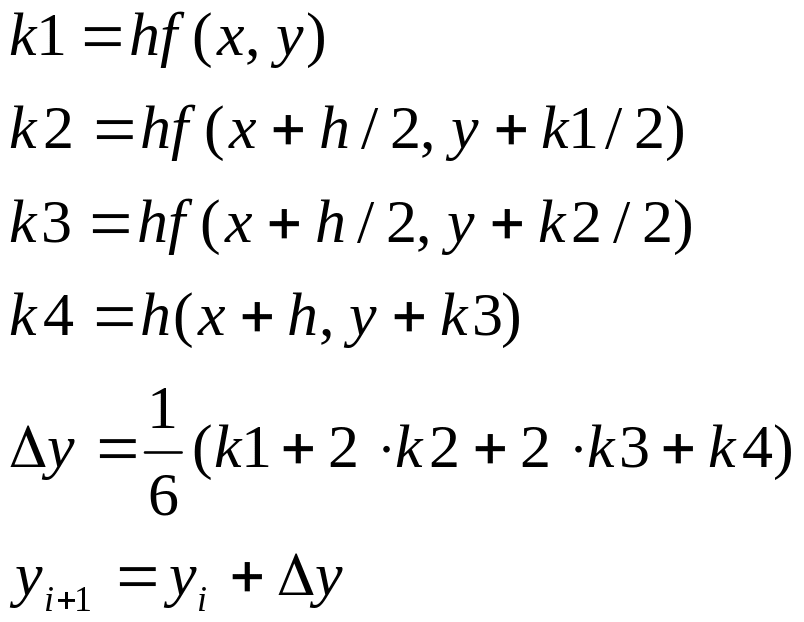
Заданный диапазон изменения аргумента [0,7;3,7] разобьем на
10 равных отрезков (шаг h=0.3000).
Получаем таблицу значений искомой функции Y(x):
№ х y
----------------------------------
0 0.7000 1.30000
1 1.0000 1.59158
2 1.3000 2.13405
3 1.6000 2.95870
4 1.9000 4.06472
5 2.2000 5.42431
6 2.5000 6.99131
7 2.8000 8.71085
8 3.1000 10.52825
9 3.4000 12.39548
10 3.7000 14.27493
График искомой функции:
