Порядок выполнения работы

1. Проверить установку прибора на нуль. Для этого при отсутствии в камере трубки с раствором, вращая головку винта 6, добиться одинаковой освещенности обеих половин поля зрения (установить на ми­нимум освещенности, а не на максимум). При этом нулевые деления шка­лы и нониуса должны совпадать.

2. Вставить трубку с раствором сахара известной концентрации С₁ в камеру, добиться равномерной освещенности поля зрения. Произвести отсчет по лимбу и нониусу и записать значение α₁ в таблицу. Сбить настройку и снова добиться равномерной освещенности. Измерения про­извести пять раз и результаты измерений занести в таблицу 1 (графа α_1i ).

3. Вставить трубку с раствором сахара неизвестной концентрации и произвести измерения по пункту 2. Результаты измерений занести в таблицу 1 (графа α_2i ).

Таблица 1

Номер измерения	α1i, … º.	Δα1,… º.	α2i, … º.	Δα2, … º.	<С2>, %	Δ С2, %	ε, %
1
2
3
4
5

4. Вычислить <α₁>, <α₂> и рассчитать неизвестную концентрацию раствора сахара по формуле (4), а Δα₁ и Δα₂ - по методу нахож­дения погрешностей при прямых измерениях, причем Δα_1приб= Δα_2приб= 0,05⁰. Определить абсолютную и относительную погрешности величи­ны С₂ по правилам нахождения погрешностей при косвенных измерениях.

Контрольные вопросы

1. Естественный и поляризованный свет.

2. Призма Николя.

3. Закон Малюса.

4. Оптически активные вещества.

5. Использование вращения плоскости колебаний в работе для определения концентрации сахара в растворе:

а) принцип устройства сахариметра;

б) образование двойного поля;

в) определение концентрации сахара.

Лабораторная работа 7-11 Определение показателя преломления вещества по углу Брюстера

Цель работы: 1) познакомиться со способом получения поляризованного света с помощью поляроида; 2) пронаблюдать отражение от стекла света с различной ориентацией плоскости колебаний; 3) определить показатель преломления вещества призмы по углу Брюстера.

Приборы и принадлежности: осветитель (или лазер) 0, поляризатор во вращающейся оправе П2, стеклянная призма Пр 1 (или Пр 2), гониометрический столик ГС, диафрагма Д (рис. 3).

Теоретические сведения

Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других - как поток фотонов. В яв­лении поляризации проявляется волновая природа света.

Электромагнитные волны поперечны: векторы напряженностей электри­ческого и магнитного полей и колеблются перпендикулярно вектору скорости распространения волны и взаимно перпендикулярны. Вектор на­пряженности электрического поля называют световым вектором.

В естественном свете (т. е. свете, испускаемом обычными источника­ми) имеются колебания вектора , совершающиеся в самых различных на­правлениях, перпендикулярных к лучу. Эти колебания быстро и беспоря­дочно сменяют друг друга. Свет, в котором направления колебаний век­тора упорядочены каким-либо образом, называется поляризованным. Упорядоченность может заключаться в том, что вектор поворачивает­ся вокруг луча, одновременно пульсируя по величине, при этом конец вектора описывает эллипс. Такой свет называется эллиптически поляризованным. Если конец вектора описывает окружность, свет называет­ся поляризованным по кругу. Если колебания светового вектора проис­ходят только в одной плоскости, то свет называется плоскополяризованным.

Плоскость, в которой колеблется световой вектор в плоскополяризованной волне, называется плоскостью колебаний.

Плоскополяризованный свет можно получить из естественного с по­мощью поляризаторов - приборов, которые свободно пропускают колебания, параллельные плоскости, которую называют плоскостью поляризатора (плоскостью пропускания). Если поляризатор идеальный, то он полностью задерживает колебания, перпендикулярные к его плоскости. На выходе из несовершенного поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями других направлений. Та­кой свет называется частично поляризованным.

В качестве поляризатора в данной работе используется поляроид. По­ляроиды представляют собой тонкие пленки из целлофана или целлулоида, в которые вкраплены тонкие иголки из минерала герапатита. Герапатит - двоякопреломляющее вещество с очень сильным дихроизмом в области ви­димого света. При изготовлении поляроидов все иголки - кристаллики герапатита (сульфата йодистого хинина) - ориентируются приблизительно в одном направлении, благодаря чему пленка становится поляризатором, т. е. пропускает волны с колебаниями одного направления и поглощает волны с перпендикулярными колебаниями.

Частично поляризованный свет, как и естественный, можно предста­вить в виде наложения двух некогерентных плоско- поляризованных волн с взаимно перпендикулярными плоскостями поляризации. Отличие состоит в том, что в случае естественного света интенсивность этих волн одина­кова, а в случае частично поляризованного - разная.

Если частично поляризованный свет пропустить через поляризатор, то при вращении его вокруг направления распространения света интенсивность прошедшего света будет изменяться в пределах от I_max до I_min.

(1)

называется степенью поляризации и характеризует меру поляризации света. В этой формуле I_max и I_min - максимальная и минимальная интенсивности света, соответствующие двум взаимно перпендикулярным компонентам вектора .

Если естественный свет направить на границу раздела двух диэлект­риков, то часть его отражается, а часть преломляется. При этом отра­женная и преломленная волны оказываются частично поляризованными. В отраженной волне преобладают колебания, перпендикулярные к плоскости падения света (на рис. 1 эти колебания обозначены точками), в преломленной волне преобладают колебания, параллельные плоскости падения света (на рис. 1 - двусторонние стрелки). При этом степень поляризации волн зависит от угла падения и показателя преломления второй среды относительно первой.

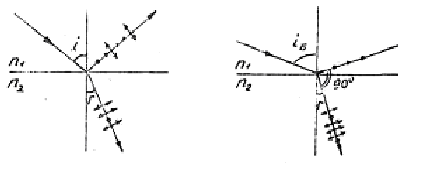
Рис. 1 Рис. 2

При угле падения i_б, удовлетворяющем условию

, (2)

где n₂₁ - относительный показатель преломления второй среды относи­тельно первой, отраженная волна полностью поляризована, она содержит только колебания, перпендикулярные к плоскости падения света. Степень поля­ризации преломленной волны при угле падения i_б достигает наиболь­шего значения. Однако эта волна поляризована только частично, в ней преобладают колебания, параллельные плоскости падения света, но имеются также и перпендикулярные.

Соотношение (2) носит название закона Брюстера, а угол i_б называют углом Брюстера. При падении света под углом Брюстера отражен­ная и преломленная волны распространяются взаимно перпендикулярно.

Степень поляризации отраженной и преломленной волн при различ­ных углах падения света на границу раздела двух диэлектриков можно получить с помощью формул Френеля. Эти формулы устанавливают соотношение между амплитудами падающей, отраженной и преломленной световых волн:

(3)

В формулах (3) i - угол падения, r - угол преломления световой волны, А, А^’ и А^” - амплитуды падающей, отраженной и преломленной све­товых волн, соответственно, символы «║» и «┴» соответствуют колебаниям светового вектора, совершающимся в плоскости падения луча и в плоскости, перпендикулярной к ней, т. е. падающая, отраженная и преломленная волны в этих формулах представлены в виде наложения двух некогерентных волн со взаимно перпендикулярными колебаниями светово­го вектора.

Из первой формулы (3) получается, что при (i+r) =.π/2, т. е. при I = i_б амплитуда обращается в нуль. Следовательно, в отраженной волне присутствуют лишь колебания, перпендикулярные к плоскости падения, - отраженная волна полностью поляризована. Таким образом, закон Брюстера непосредственно вытекает из формул Френеля. В данной работе закон Брюстера используется для определения показа­теля преломления стекла.