Лабораторная работа №1.5
Задание: Используя логические элементы И-ИЛИ, И-ИЛИ-НЕ, ИЛИ-НЕ, разработать алгоритмы определения отношений A<B для n-разрядных кодов. В соответствии с алгоритмами построить и тестировать КЛС на элементах ИЛИ-НЕ. Используя отношения равенства A=B и их схемную реализацию на элементах ИЛИ-НЕ построить последовательную схему для отношения неравенства A<B.
Определение A<B для 3-х разрядных кодов на элементах ИЛИ-НЕ:
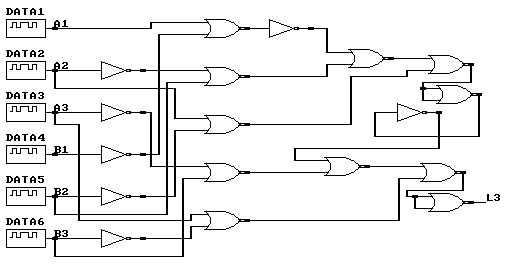
Синтез последовательностных схем (элементов памяти), использующих в качестве элементной базы клс. Синтез асинхронных триггеров.
Синтез асинхронных триггеров основан на использовании функции переходов запоминающего элемента с двумя устойчивыми состояниями. Такую функцию представим в виде таблицы переходов:
Sn |
Rn |
Qn |
Qn+1 |
0 0 |
0 0 |
0 1 |
0 1 |
0 1 |
1 0 |
0 1 |
0 1 |
1 0 |
0 1 |
0 1 |
1 0 |
1 1 |
1 1 |
0 1 |
- - |
n-автоматное (целочисленное) время
Q-состояние
1. При отсутствии входных возмущений Sn или Rn запоминающий элемент сохраняет исходное состояние: Qn+1 = Qn (сохраняется)
2. Если входной сигнал действует на вход, наименование которого совпадает с исходным состоянием, то такое состояние подтверждается в реакции на возмущение. Qn+1 = Qn (подтверждается)
3. Элемент изменяет состояние на противоположное, если возмущение действует на вход, соответствующий требуемому состоянию. Qn+1 =Qn
4. Состояние запоминающего элемента при одновременном воздействии на входы R и S произвольно, поэтому при синтезе различных разновидностей запоминающих элементов этому состоянию можно задавать различные комбинации значений истинности Qn+1 ,Qn+1.
Синтез первой минимальной формы для запоминающего элемента.
Qn+1 |
Q |
0 1 0 1 |
0 1 1 0 |
n+1
Перенесем содержимое переходов в карту Карно и заменим два последних состояния значениями 1 1.
-
Sn , Rn
Qn
00 01 11 10
0
1
0
0
1
1
1
0
1
1
З
апишем
минимальную форму функции перехода.
Реализуем это выражение на элементах И-ИЛИ-НЕ, НЕ
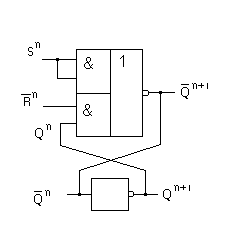
Построим расширенную таблицу переходов для вычисления функций Qn+1 ,Qn+1 и перенесем каждую пару этих вычисленных состояний в расширенную матрицу Карно.
-
Sn , Rn
Qn , Qn
00 01 11 10
00
01
11
10
11
11
10
10
(01)
(01)
00
00
00
01
00
00
(10)
11
(10)
(10)
Установившимися состояниями запоминающего элемента называются такие комбинации значений (Qn+1 ,Qn+1), которые соответствуют исходным состояниям схемы Qn ,Qn. В матрице отметим эти состояния скобками.
При отсутствии входных возмущений Sn , Rn , запоминающий элемент равновероятно находится в одном из следующих состояний: нулевом 01 или единичном 10.
Устойчивыми считают те из установившихся состояний, которые соответствуют логике работы запоминающего элемента (ЗЭ).
При воздействии на схему сигнала Rn = 1, ЗЭ переходит в нулевое состояние => Qn+1 ,Qn+1 ~ 01; аналогично при воздействии сигнала Sn =1, элемент переходит в единичное состояние => Qn+1 ,Qn+1 ~ 10.
Данный ЗЭ переходит в единичное состояние при одновременном воздействии на него сигналов S и R, при этом он получил название S - триггера и его работа может быть описана следующей временной диаграммой.
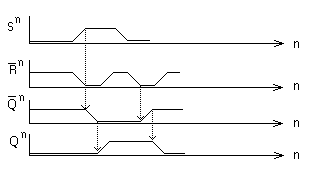
Выбор элементной базы для построения ЗЭ в определенных рамках произволен и определяется разработчиком. Все остальные этапы синтеза могут быть формализованы и требуют обязательного анализа установившегося и устойчивого состояний синтезируемого элемента памяти.
Выполним предыдущие этапы синтеза для примера схемы памяти, построенной на элементах И-НЕ. При условии возмущения ее инверсными значениями сигналов Sn и Rn.
-
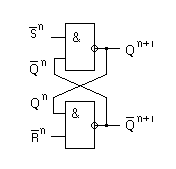
10 Экв.
Sn
Rn
Qn
Qn
Qn+1
Qn+1
0
0
0
0
0
1
1
1
0
0
0
1
0
1
2
0
0
1
0
1
0
3
0
0
1
1
0
0
4
0
1
0
0
1
1
5
0
1
0
1
0
1
6
0
1
1
0
1
1
7
0
1
1
1
0
1
8
1
0
0
0
1
1
9
1
0
0
1
1
1
10
1
0
1
0
1
0
11
1
0
1
1
1
0
12
1
1
0
0
1
1
13
1
1
0
1
1
1
14
1
1
1
0
1
1
15
1
1
1
1
1
1
-
Sn , Rn
Qn , Qn
00 01 11 10
00
01
11
10
11
11
11
11
(01)
(01)
11
11
00
01
(11)
10
(10)
11
11
(10)
Одновременное воздействие сигналов на инверсные входы схемы Sn и Rn запрещено, так как исключает общепринятое состояние триггера.
Поэтому функцию перехода этого триггера необходимо дополнить уравнением запрета.
Построим временную диаграмму для ЗЭ с инверсными входами.
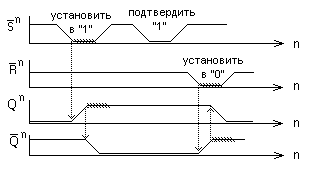
Каждая из возможных разновидностей форм построения ЗЭ может иметь структурные вариации, определяемые конкретными используемыми элементами. Назначение этих вариаций должно быть обосновано конкретным применением синтезируемого элемента.