Условие нормировки
,
использован бином Ньютона
.
Исаак Ньютон (1642–1727)
Среднее число частиц в объеме V
,
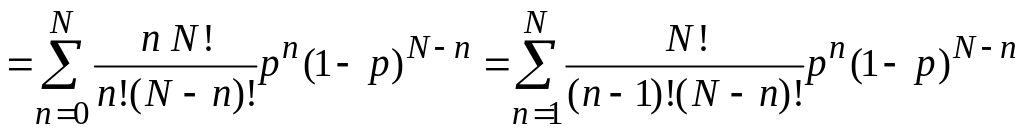где учтено
;
.
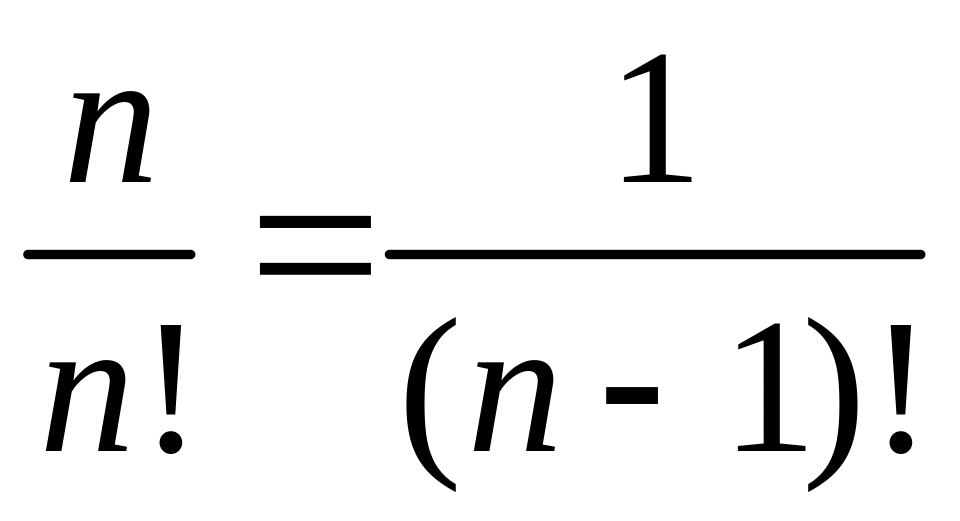Замена
и бином Ньютона дают
=
=
.
Результат
(1.15)
очевиден,
поскольку
– средняя концентрация.
Из (1.15) вероятность признака у одного элемента
.
(1.16)
Из
биномиального распределения получаем
– если в
некотором состоянии наблюдается в
среднем
частиц, то вероятность наблюдения n
частиц
равна
,
(1.17)
причем
,
(1.17а)
.
(1.17б)
График распределения
а б
Распределения
биномиальное (а) и Пуассона (б)
для N
= 10,
,
р
= 0,45
Распределение Пуассона
Считаем
вероятность появления признака у одной
частицы малой
и общее число частиц большим
.
Тогда, если
признак имеют в среднем
частиц, то его вероятность для n
частиц
.
(1.18)
Результат получил из биномиального распределения Пуассон в 1837 г.
Симеон Дени Пуассон (1781–1840)
Доказательство:
Записываем биномиальное распределение (1.17)
,
где учтено
.
При
используем
,
,
,
и получаем (1.18).
Условие нормировки
Используем
N
– велико,
,
,
получаем
.
Частные и рекуррентные соотношения
,
,
,
.
(1.18а)
График распределения
а б
Распределения биномиальное (а) и Пуассона (б) для N = 10, , р = 0,45
нормальное распределение Гаусса
При
и относительно малом отклонении от
среднего
выполняется нормальное
распределение
.
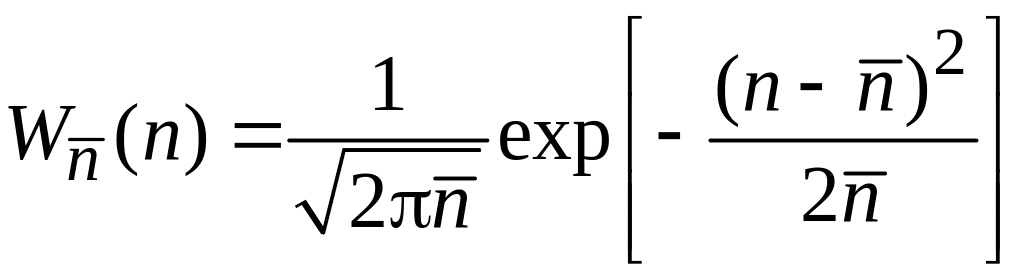(1.19)
Резултат получил Гаусс в 1809 г.
Карл Фридрих Гаусс (1777–1855)
Доказательство:
Распределение Пуассона
логарифмируем
.
Используем формулу Стирлинга (будет доказана в курсе ММФ)
,
при
,
,
тогда
.
Учитывая
,
,
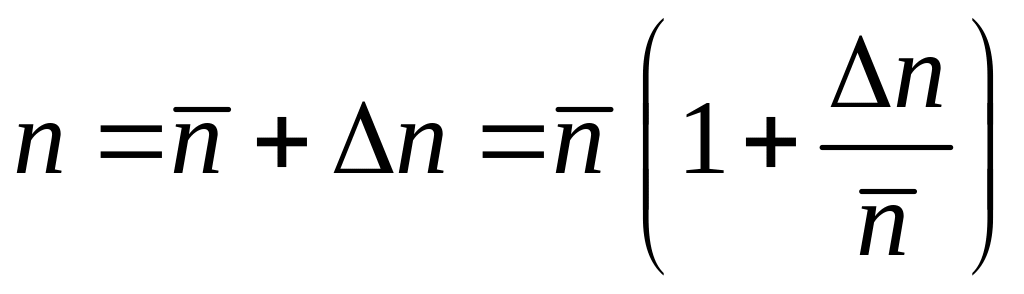разлагаем в ряд
.
В результате
.
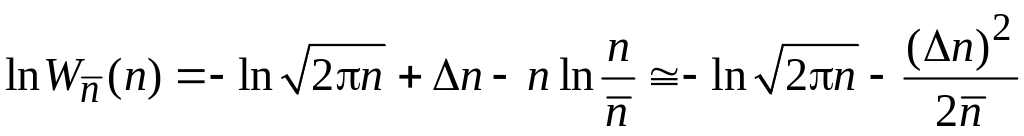Заменяя
и потенцируя, получаем (1.19).
Условие нормировки
На основании считаем n квазинепрерывным, тогда
– плотность
вероятности,
Условие нормировки получает вид
,
где
;
при
;
;
учтено
.
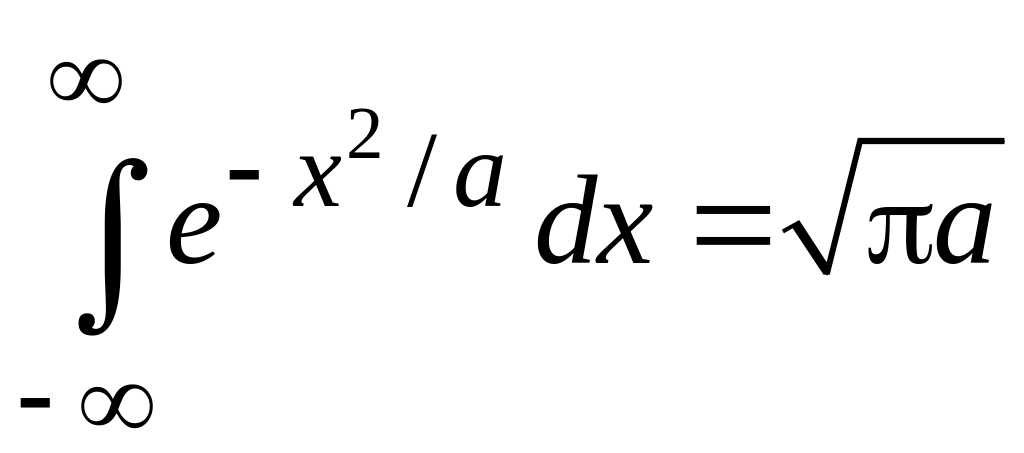Среднее значение
,
,
,
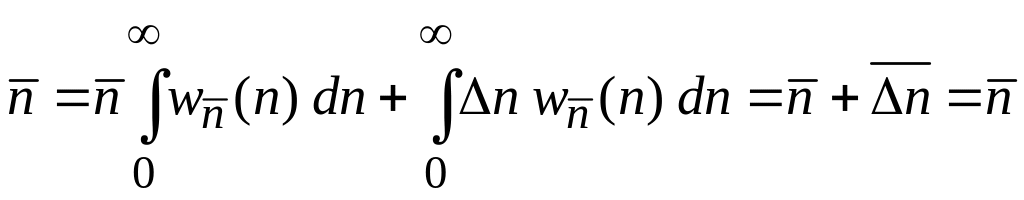где
.
Дисперсия
,
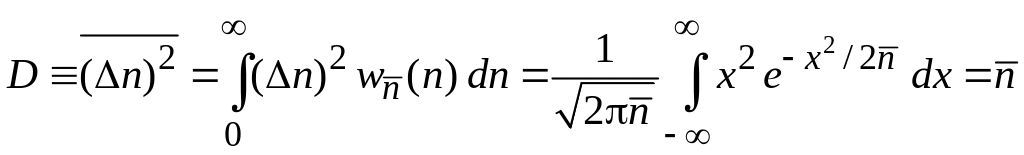где
,
,
и учтено
.
В результате
.
(1.20)
Из (1.19) и (1.20) плотность вероятности
.
(1.21)
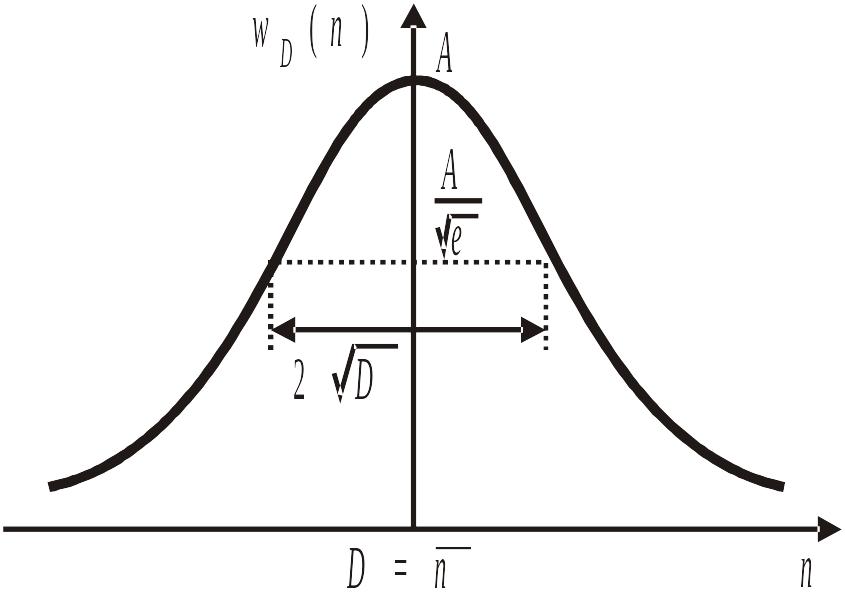
Распределение
Гаусса,
Центральная предельная теорема – при суммировании большого числа независимых случайных величин, имеющих различные распределения, результирующее распределение близко к распределению Гаусса.
Теорема обосновывает применимость нормального распределения к многочисленным случайным процессам. Теорему доказал Ляпунов в 1901 г.
Александр Михайлович Ляпунов (1857–1918)